サポートベクトルマシーン回帰 (SVR) メモ

サポートベクトルは分類機としてもちいられてきた(SVC)が、回帰にも応用できる。 ここでは、前節と同様にPRMLテキストをもとに、SVRについて簡単に解説する。

目的変数yy、説明変数{xn}\{\boldsymbol{x_n}\}の関係を、非線形関数ϕ(xn)\boldsymbol{\phi}(\boldsymbol{x_n})を用いて (ここでnnはn番目のデータを表す)

yn=y(xn)=ωTϕ(x) y_n = y(\boldsymbol{x_n}) = \boldsymbol{\omega}^T\boldsymbol{\phi(\boldsymbol{x})}

と表されるとする。ω\boldsymbol{\omega}, ϕ\boldsymbol{\phi}の次元(要素数)は場合による。

観測値tnt_nと予測値yny_nとの差が小さくなるようにwn\boldsymbol{w_n}をきめる。つまり、

12∑n=1N{yn−tn}2+λ2∣∣w∣∣2 \frac{1}{2}\sum_{n=1}^N \{y_n -t_n\}^2 + \frac{\lambda}{2} || \boldsymbol{w} ||^2

「疎な解」を得るため(ほとんどのデータは予測値とほぼ同じと考え)、第１項の2乗関数を次のようなϵ\epsilon許容誤差関数(ϵ\epsilon-insensitive error function)で置き換える(図7.6)。

Ee(y(x)−t)={0∣y(x)−t∣<ϵ∣y(x)−t∣−ϵother E_e (y(\boldsymbol{x})-t) = \left\{ \begin{array}{ll} 0 & |y(\boldsymbol{x}) - t| < \epsilon \\\\ |y(\boldsymbol{x}) - t| - \epsilon & {\rm other} \end{array} \right.

7.6図

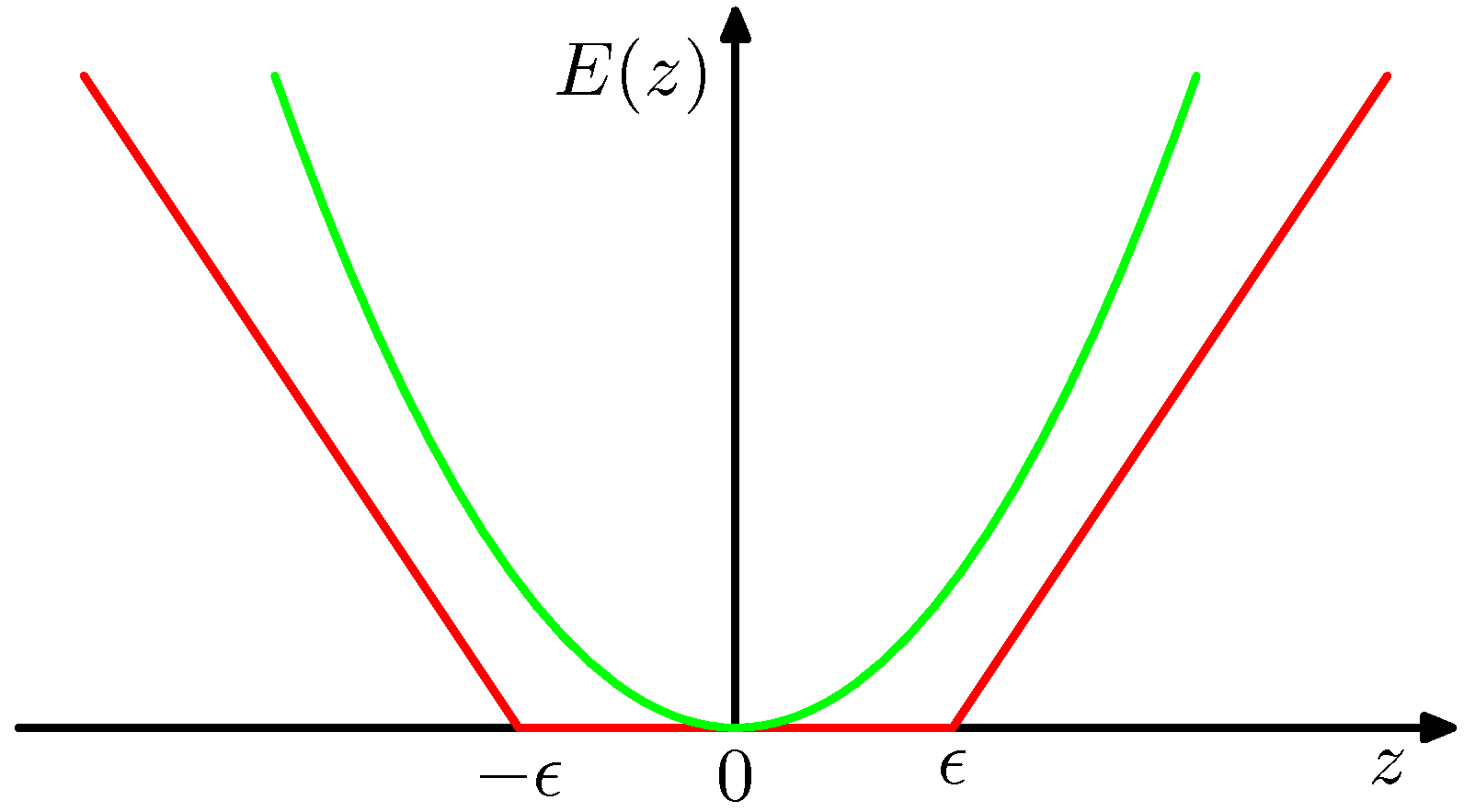
つまり、

C∑n=1NEe(y(xn)−tn)+12∣∣w∣∣2 C\sum_{n=1}^N E_e(y(\boldsymbol{x_n})-t_n) + \frac{1}{2}||\boldsymbol{w}||^2

を最小にするw\boldsymbol{w}をもとめる。

許容誤差関数を使う代わりに、スラック変数を導入して表現する。±ϵ\pm \epsilonのチューブの外側に高いコストを与えるように、ξ\xiとξ^\hat{\xi}を定義する。図に示すように、 tn>y(xn)+ϵt_n > y(\boldsymbol{x_n}) + \epsilon に対してはξn>0\xi_n > 0を、 tn<y(xn)+ϵt_n < y(\boldsymbol{x_n}) + \epsilon に対しては,ξ^n<0\hat{\xi}_n < 0を対応させる。

7.7図

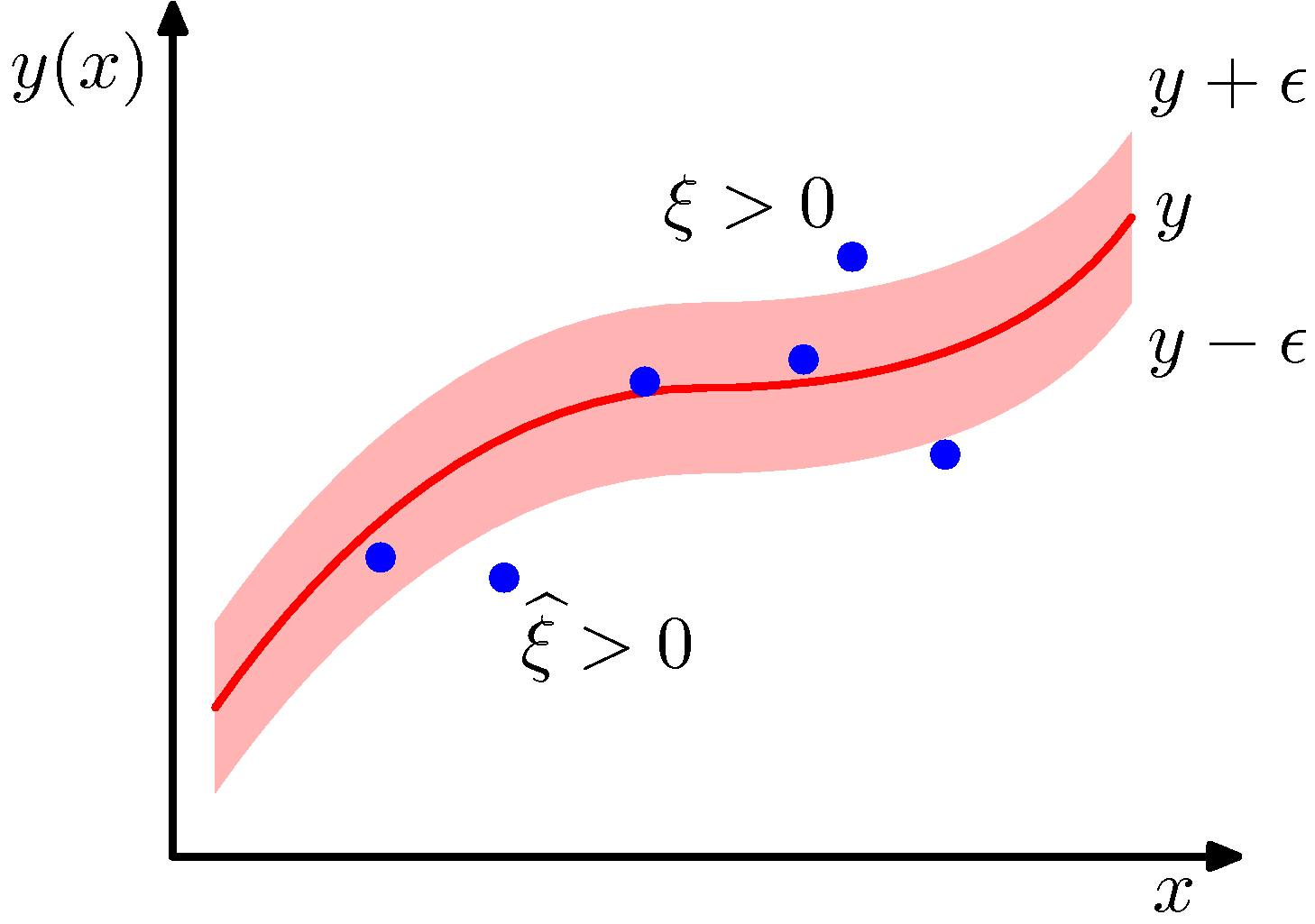
制約条件として

tn≤y(xn)+ϵ+ξn,tn≥y(xn)−ϵ−ξ^n(1) t_n \le y(\boldsymbol{x_n}) + \epsilon + \xi_n,\quad t_n \ge y(\boldsymbol{x_n}) - \epsilon - \hat{\xi}_n \tag{1}

を課す。このようなスラック変数を用いると、SVRの誤差関数は

C∑n=1N(ξn+ξ^n)+12∣∣w∣∣2(2) C\sum_{n=1}^N (\xi_n + \hat{\xi}_n) + \frac{1}{2}||\boldsymbol{w}||^2 \tag{2}

と表される。また、条件

ξn≥0,ξ^n≥0(3)\xi_n \ge 0, \quad \hat{\xi}_n \ge 0 \tag{3}

も必要である。誤差関数(2)を条件(1)と(3)のもとで最小化する係数を求める。

ラグランジュの未定定数an≥0a_n\ge 0, a^n≥0\hat{a}_n \ge 0, μ≥0\mu \ge 0, μ^≥0\hat{\mu} \ge 0を使って

L=C∑n=1N(ξn+ξ^n)+12∣∣w∣∣−∑n=1Nan(ϵ+ξn+yn−tn)−∑n=1Na^n(ϵ+ξ^n+yn−tn) L = C\sum_{n=1}^{N} (\xi_n + \hat{\xi}_n) + \frac{1}{2}||\boldsymbol{w}|| - \sum_{n=1}^N a_n (\epsilon + \xi_n + y_n - t_n) - \sum_{n=1}^N \hat{a}_n (\epsilon + \hat{\xi}_n + y_n - t_n)

の極値問題を解く。極値条件は

∂L∂w=0よりw=∑n=1N(an−a^n)ϕ(xn)(4) \frac{\partial L}{\partial \boldsymbol{w}} = 0\quad \text{より}\quad \boldsymbol{w} = \sum_{n=1}^N (a_n - \hat{a}_n)\boldsymbol{\phi}(\boldsymbol{x_n}) \tag{4}

∂L∂b=0より∑n=1N(an−a^n)=0(5) \frac{\partial L}{\partial b} = 0\quad \text{より}\quad \sum_{n=1}^N (a_n - \hat{a}_n) = 0 \tag{5}

∂L∂ξn=0よりan+μ^n=0(6) \frac{\partial L}{\partial \xi_n} = 0\quad \text{より}\quad a_n + \hat{\mu}_n = 0 \tag{6}

∂L∂ξ^n=0よりa^n+μ^n=0(7) \frac{\partial L}{\partial \hat{\xi}_n} = 0\quad \text{より}\quad \hat{a}_n + \hat{\mu}_n =0 \tag{7}

これらの条件を用いてLLを変形すると、{an}\{a_n\}と{a^n}\{\hat{a}_n\}を変数としたLLの極値問題に帰着できる。

C∑(ξn+ξ^n)−∑(μnξn+μ^nξ^n)−∑anξn−∑a^nξ^n=0 C\sum (\xi_n + \hat{\xi}_n) - \sum (\mu_n\xi_n + \hat{\mu}_n\hat{\xi}_n) - \sum a_n\xi_n - \sum \hat{a}_n\hat{\xi}_n = 0

∣∣ω∣∣2=∑n=1N∑m=1N(an−a^n)(am−a^m)k(xn,xm) ||\omega ||^2 = \sum_{n=1}^N\sum_{m=1}^N (a_n -\hat{a}_n)(a_m -\hat{a}_m) k(\boldsymbol{x}_n, \boldsymbol{x}_m)

であるから

L^(a,a^)=−12∑n=1N∑m=1N(an−a^n)(am−a^m)k(xn,xm)−ϵ∑n=1N(an+a^n)+∑n=1N(an−a^n)tn(8) \hat{L} (\boldsymbol{a}, \hat{\boldsymbol{a}}) = -\frac{1}{2}\sum_{n=1}^N\sum_{m=1}^N (a_n -\hat{a}_n)(a_m -\hat{a}_m) k(\boldsymbol{x}_n, \boldsymbol{x}_m) - \epsilon\sum_{n=1}^N (a_n + \hat{a}_n) + \sum_{n=1}^N (a_n - \hat{a}_n)t_n \tag{8}

ここで、カーネルの定義

k(xn,x′m)=ϕ(x)Tϕ(x′)(9) k(\boldsymbol{x}_n, \boldsymbol{x'}_m) = \boldsymbol{\phi}(\boldsymbol{x})^T \boldsymbol{\phi}(\boldsymbol{x'}) \tag{9}

を用いた。 an≥0a_n \ge 0, a^n≥0\hat{a}_n \ge 0とμn≥0\mu_n \ge 0, μ^n≥0\hat{\mu}_n\ge 0および(6),(7)の条件を合わせると矩形制約(box constraint)

0≤an≤C,0≤a^n≤C 0\le a_n \le C,\quad 0\le \hat{a}_n \le C

が成り立つ。これと(5)式の条件のもとでLLを最大にする問題になる。

得られたana_n, a^n\hat{a}_nから、予測値は

y(x)=∑n=1N(an−a^n)k(x,xn)+b(10) y(\boldsymbol{x}) = \sum_{n=1}^N (a_n - \hat{a}_n)k(\boldsymbol{x}, \boldsymbol{x}_n) + b \tag{10}

により計算される。

不等式制約下での極値条件(KKT条件)、つまりラグランジュ未定乗数と対応する制約式の積がゼロという条件は

an(ϵ+ξn+yn−tn)=0(11) a_n (\epsilon + \xi_n + y_n - t_n) =0 \tag{11}

a^n(ϵ+ξ^n+yn−tn)=0(12) \hat{a}_n (\epsilon + \hat{\xi}_n + y_n - t_n) =0 \tag{12}

(C−an)ξn=0(13) (C - a_n)\xi_n = 0 \tag{13}

(C−a^n)ξ^n=0(14) (C - \hat{a}_n)\hat{\xi}_n = 0 \tag{14}

これらの式から、ana_nがゼロ以外の値をとるのは、()()の中がゼロのとき、すなわちデータ点がチューブの上境界上か外側上にあるときであり、a^n\hat{a}_nがゼロでないのは、チューブの下境界上か外側下にある場合である。

また、この2つが同時に成り立つことはないので、すべてのデータ点xn\boldsymbol{x}_nに対してana_n, a^n\hat{a}_nのどちらかはゼロである。

よって、予測に寄与するのは、チューブの外側の点である。つまり、チューブの外側の点がサポートベクトルであるといえる。データが非常にばらついていて、チューブの外のデータ点がたくさんあるときはあまり良い推定が得られない(と思う。かえって線形回帰の方が良い場合もあるだろう)。

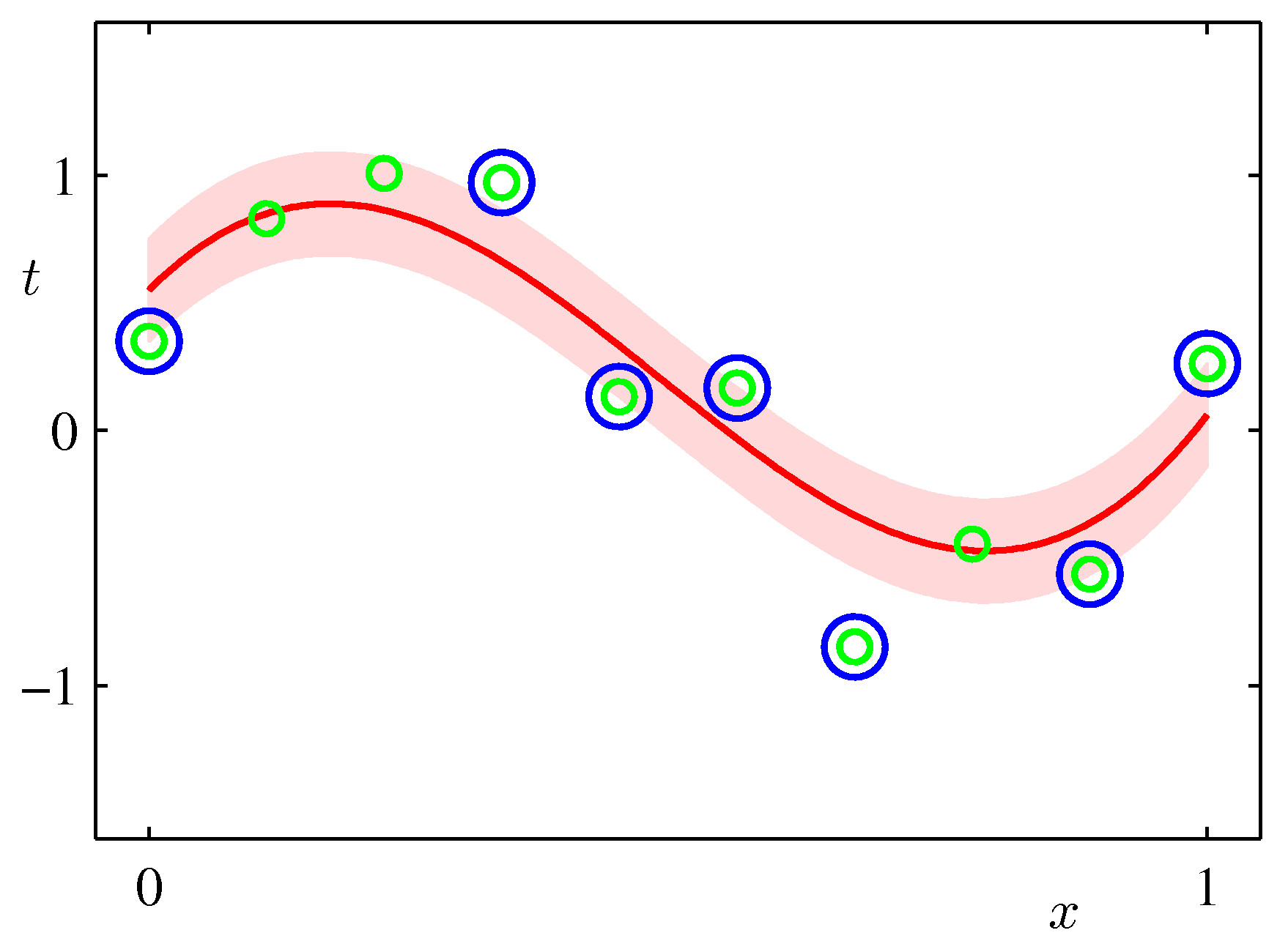
7.8図 〇がついているデータがサポートベクトル

パラメータbbについて

0<an<C0 < a_n <Cのとき、(11)よりξn=0\xi_n = 0。(11)式よりϵ+yn−tn=0\epsilon + y_n - t_n=0である。これを

y(x)=ωTϕ(x)+b y(\boldsymbol{x})= \boldsymbol{\omega}^T\boldsymbol{\phi}(\boldsymbol{x}) + b (テキストでは(7.1)

b=tn−ϵ−ωTϕ(x)=tn−ϵ−∑m=1N(am−a^m)k(xn,xm) b = t_n - \epsilon - \boldsymbol{\omega}^T\boldsymbol{\phi}(\boldsymbol{x}) = t_n - \epsilon - \sum_{m=1}^N (a_m - \hat{a}_m)k(\boldsymbol{x_n}, \boldsymbol{x}_m)

が得られる。実際には、このようにして得られたbbの平均値を用いる。

チューブの幅ϵ\epsilonはパラメータであるが、これの代わりに、チューブの外にあるデータ数の割合の上限ν\nuを指定する方法もある。(Scholkoph, et.al. (2000))

パラメータν\nu, CCは交差検定によりセットすることが多い。

scikit-learnでは、グリッドサーチやランダムサーチにより決定している。