"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"%matplotlib inline"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"# Lecture on Numerical Simulation Methods (1)\n",
"\n",
"Goal: Learning\n",
" - how to use jupyter(ipython notebook)\n",
" - type of cells: \"Markdown\" and \"code\"\n",
" - elements of \"Markdown\"\n",
" \n",
" - methods to solve ordinary differential equations (ode) and functions in scipy (scientific python) for ode\n",
" \n",
"An tutorial page about jupyter: http://qiita.com/taka4sato/items/2c3397ff34c440044978\n",
"\n",
"It is recommended to create a new notebook, copy&paste sample codes in the following and try to use them.\n",
"(新しいノートブックを作成し、下のサンプルコードをコピーして実行、改変を試してみることを推奨する)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## Tips on python coding\n",
"\n",
"\n",
" - Grouping statements is described by indentation (\"space\" or \"tab\")\n",
" - Flow control statements \"for\", \"while\" and \"if\" are somewhat different from those of C, Java and fortran.\n",
" See e.g. http://docs.python.jp/2/tutorial/\n",
" - To define a function, use \"def\" statement.\n",
" - If you would like to plot on a new window, execute \"%matplotlib auto\".\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Euler Method for ordinary differential equations"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"The simplest numerical method for solving a differential equation is called the Euler Method, which is a discretization of the differentiation.\n",
"For the definition of the differentiation\n",
"\\begin{equation}\n",
" \\frac{dx}{dt} = \\lim_{h \\rightarrow 0} \\frac{x(t + h ) - x(t)}{h } ,\n",
"\\end{equation}\n",
"we take a finite $h$.\n",
"For a differential equation\n",
"$$\n",
" \\frac{dx}{dt} = f(x),\n",
"$$\n",
"we calculate numerically $x(t+h)$ from $x(t)$ by\n",
"\\begin{equation}\n",
" x(t + h ) = x(t) + h f(x(t))\n",
"\\end{equation}\n",
"\n",
"### Euler Method for a harmonic oscillator\n",
"\n",
"Let's try to calculate a harmonic oscillator equation\n",
"$$\n",
"\\begin{eqnarray}\n",
" \\frac{dx}{dt} & = & v \\\\\n",
" \\frac{dv}{dt} & = & - kx\n",
"\\end{eqnarray}\n",
"$$\n",
"by using the Euler method.\n",
"\n",
"note:\n",
"\n",
"To solve heigher-order differential equations, we rewrite them as a first-order equations by defining some new variables.\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAsMAAAFCCAYAAAAUiNCiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzsnXdYVGf6hu8jRcAuYEexo6Kx9xhNbOlG04zpdTc92c1mk9305JfdTdtN7z0mRhOjpthLbIm9BUWxAlYQsdAEzu+PZ0ZQQWZGpul3X9dcB2YOM+ebwjzn/Z7veS3btjEYDAaDwWAwGM5Gqvj7AAwGg8FgMBgMBn9hxLDBYDAYDAaD4azFiGGDwWAwGAwGw1mLEcMGg8FgMBgMhrMWI4YNBoPBYDAYDGctRgwbDAaDwWAwGM5ajBg2GAwGg8FgMJy1GDFsMBgMBoPBYDhrMWLYYDAYDAaDwXDWEurLB4uJibHj4+N9+ZAGg8FQaSxfvjzDtu1Yfx+HLzH/tw0GQ7Di6v9sn4rh+Ph4li1b5suHNBgMhkrDsqzt/j4GX2P+bxsMhmDF1f/ZxiZhMBgMBoPBYDhrMWLYYDAYDAaDwXDWYsSwwWAwGAwGg+Gsxaee4bI4evQoaWlp5OXl+ftQKpWIiAiaNGlCWFiYvw/FYDAYDAaDwVAOfhfDaWlp1KhRg/j4eCzL8vfhVAq2bZOZmUlaWhrNmzf39+EYDAaDwWAwGMrB7zaJvLw8oqOjzxghDGBZFtHR0WdctdtgMBgMBoPhTMPvYhg4o4SwkzNxTAaDwWAwGAxnGgEhhg0Gg8FgMBgMBn9gxLDBYDAYDAaD4azF7wvoDAbDWcjKlbBvHwwZAsZSZDCceRQdhdxMyM+Go0egMAeOOi9HwC4C23bsbJf8XUhVCIuC0MiSS1g1iKwLEXUhxCQ0GSofI4YrIDc3l+HDhzN79mxCQkJIS0tj4cKFXHPNNRQUFDB48GBmz55NaKh5Kg0Gl5g/HwYOhOJiePVVeOghfx+RwWBwlaICOJQGB3fAwVTHdgccToecDMh1XPKzvfP44TUhKgYioyGqHtRoAjXioGactjWaQM2mEFrVO49vOCMxCq4CPv74Y0aOHElISAgAs2bNIikpiWuuuYbw8HAuuOACxo0bx5gxY/x8pAZDkPD449C4MTRrBs89B3feCdWq+fuoDAZDaXIyIDMJMjfA/mTHdgMc2MpxlVxwiNLGEBkLdVpCZIwuUTFQtZYqu2HVIDSqpOp7rMLrmBmyLFWKi/JVPS7M1eVoDhw9DLn7VWnOc2xzM+HwTtj5u8R3aawqUKs51G3ruLSB6ASI7SgRbTCcQGCJ4QcfhFWrKvc+O3eG//63wt0GDRrE448/zpAhQ/jnP//JwYMHef311/nqq68YO3YsAAsWLODhhx+mdu3aTJs2jYkTJzJixAgee+wxI4YNvuHQIXjiCahdW1vHSVrQsGULLFgAL74IffqoQvzjj3DNNf4+MoPh7MS2JSr3rIDdK7Tds0LVXyehkRKVDXtC++uhVryqrzWbqhIbFgnFRaWEakaJYD20U2K2tMAtzIXC0tGjpQRxlVCHeI4qJZ6jIKIO1O8swR3lENsRtSV8j+bqeA+lqlp9YLME/P5k2DFHj+ekRhzU7wL1u5ZsazbxxTNtCGACSwz7kWeeeYYnn3ySvXv3snLlSiZPnkxBQQFbtmwhPj4egP79+9OjRw9efvllEhMTASgqKmLp0qV+PHLDWcWDD8LHH+vnatXgkUf8ezzuMmWKttdeC3FxEBsLkyYZMVwJWJZ1JXA10Nu27aZl3P4Z0BZwqpBXbdue7MNDNAQCxUWQsQ5S50PaAl0OpztutFRBjTtPQjEmUb/XjNPNB3dAZjIcSIFt0yU8nQL0cDoUF5b/uKW9wGFR+h2LY1Vmp3+4uEDi1ukzLioo/z6tEIctIq5EnNdsCo37Qqdb9TNIKGdugL2rYM9KXVKmlDx2jTho0g8a94Mm/VVBrhJkhQbDaRFYYtiFCq63GDBgALZt8+qrrzJ37lxCQkLYs2cPtWvXPm6/5ORk2rZte+z3kJAQwsPDOXToEDVq1PD1YRvcpbAQgtXfvXs3fPYZPPAAbNgAL78scRxMLb/nzYPmzcFxgsmQITBnjr4IzUK602UfcDewrpzb44BBtm3nlnO74UzEtiEjCbZOg+0zIW0hFBzUbTWaQNwAaNwH6neDep1UlT24XYIxfSGs+VAV1qxNx1dzQ8JL/Lpx52pbvaHDIhFdcomoC+HVVcEtfUxF+RLmluW4zbG1qhwvRIsLVVXOy1LFubQvOWdviW85fTFs+PZ4QR4aKYtE3QSJ+nrnQMI1EslHj8DeNbB7mcaZOh/Wf6O/C68hURw/FJoPheh25v/TGU6QqoLKZ+3atezatYuYmJhjojYyMvK4LnKZmZnUqlWLsBPER35+PhERET49XoMHjBsHN98MvXrBzz9DVJS/j8g9vvkGiorgrrtg40YYMULicvBgfx+ZaxQXw6+/wqWXllzXty+MHQs7dshDbPAY27bnwSkb/tQG3rEsqwWwBvibbds5Pjo8gy/Jy4KtMySAt04rqfzWTYD2oyX0mpwrUXh4l8Tgxu9h/j9VPc3L0v5WFajdUhaJ+KHaRreFOm2gWj2J2iO74VC6w6aQBhl/lLJL7NfP+QccNok8KMo7wSJRBlXCJMrDq5f4javWcviQYx2XelCvM7S8BGo2g+oNSo7nwGZVsPdvUEV491IJZWclOKKu7BENukKD7nD+axLyB3fouUhbANtnw2zH4t7qjUqEcYvhsmwYziiMGAZ27drFmDFjmDRpEvfffz/Tpk1j2LBh1KlTh6KiIvLy8oiIiGDr1q00atTouL/NzMwkNjb2JIFsCDAOHNBCrXr1JCD/9z947DF/H5V7TJ8OCQnQrp0qq5GRMHly8IjhrVshM1MC2Inz50WLjBj2PsuA52zbTrUs6yngCaDMD4FlWXcCdwI0bXqS48IQiBzeBZt+gOTv5ZO1i6BqbYgfDM2HScjViIPM9ZD6q4Rv2kLI3qq/D6kqe0Dbqxxe2i4Ou0CY9tm/UZeksdpmpchrbBcdfxxWFYlNZxRatQaqrIZFQWgEhEQ4ItMiVAG2bcAGu1g/20Ul8WulL/nZsG8N5OyTwD6RkHCNr1YzqNVCleBmF0DXe3VdYR7sW3u8N3rpa1B8VH9fu4VOEhr3h673wZC3JI63zYCt0yFlEqz7VJ7muIHQ5gpofbkWDhqCnrNeDOfk5DBy5EheeeUV2rVrxxNPPMGjjz7KsGHDABg6dCgLFixg8ODBJCQkkJGRQWJiIu+//z59+/Zlzpw5XHTRRX4ehQ/Ytw/Gj4cLL9Q0d7Dx9ddw8CDMnq00g7fegkcfhSpB0nemsFALz5wLNSMjtQBtwQL/Hpc7rFmj7TnnlFzXsSOEh2vh7OjR/jmuswTbtu8s9et44I1T7Ps+8D5A9+7d7fL2M/iZg6mwfpyqujsX67q6baHX36DVpdCwh6q822bC/Kfk8z28U/tVqy+PbNd7JQLrd9ZCs71rVB1e9b62GeuO9+1GRqsy3HRgyQK6Y5fGut22JV7z9uvx87Ig/6CsEUX5jgpxvu7XsoAQ/S+uEiIxXa2BoypcXZaFcMc2KlZV2eIiVZ5z9sqznL1d1o6DO/RzyiTZO5yERqgqXq8zNOgmP3G9/0nY7lmlSnD6AtjyC6z7XH9zrBo8DIa9oxOLXUtg0yTYNBFm3KNLw57QdhS0u84sxAtiznoxHBUVxeLFi4/9PmDAgON+v/fee3n11VcZPHgw1atXZ8mSJcf9/dixY3nxxRd9drx+IT9fq/6TkqBBA1i3DqKDLJ7m228hMRG6doUbbtBl6VJZJoKBVauUJHHeeSXX9esHL7yg64PBr752rb74OnQouS40VNXudeXZXA2VgWVZkcDjqDJcAFwIrPDvURk8Iv8gJH8Hf3wBO+YCtqb8z30e2oxURXTvalWJZ9yrCihIRDYbrApx04GyP2RtgvRFEo5pCxWl5iQqVuKx2wMQ08ERUdZaovBQKuzfBNlb4GCaROLhnbJLHN5ZduW2srBCSmwSzpzhWvEQ3R5aXKifazSRGM/coEp45nr5prf8rOouSHRHt5eYjTsXBr2sOLb9G1U53zajpBqMBQ27Q/MLod21cN6Luu9NP0gYz30U5v5dz2uH6yWOq9by3nNgqHTOejFcEV26dGHQoEEUFRUdyxp2UlBQwIgRI45bUHdG8tVXEsJPPKFc2DfegKef9vdRuU5urqbh77tPYuzii7WdOjV4xPCyZdr26VNyXd++8uEuWwaDBvnnuNxhzRpo1erkTOHExOCqcAcRlmV9A/zLtu1VlmVlAEssy8oG0oG7/Ht0Bpexi+UBXvuJBFphHtRpBf2fhvZjJADTF8LqDyTOsrcBllIVzn1eArh+V12/bYbEW+qvJfm8VWtr3/ajtZCufmcJzsxk2Lda4nrjdyUCuHSl2FnJrdFYxxQ3oKSCW/oSXtNhk6hasg0JLxmfXaRtcZGqxgWHFclWcEg/52eXLJo7stex3aPxHN7JcdnHVcIc2cLtZdFo2BM63qzq8JE9sGc57HZcNv0Aax0JPdUbyUsdN0CCt9bXsGupKupbp8Hi52HRsxLNbUbq0vtROLBF9pE/voRfboPpd0Ory+Cc22VTsYJkBvIsxrLt05sBsyzrauAhoBDYBdxc3qKM7t2728ucX+oO1q9fT7t27U7rGAKV9evX0y4hQR22vvtO2arXX+/vw3Kf/v3l9UxKguHDISVFl2BZXTt7NlxwAfz0EzgtLZ07yz88fbp/j81V7r5bC82yskqe9927oWFDpbA88IB/j88V2rSBTp1gwoTjr3/xRVlXsrOhZk3/HJuLWJa13Lbt7v4+Dl9S1v9tg4/I2ScBvOo9Ca6IuqpMdrgBGvVS4sMfX8KGb+QZDglX9bfNFRJjYVHyu26dJtHo9AfXiINm5zuixPpJOGYmy2qx8zfdb8YfEqVQIi7rtC651G0NtVvJbpGfLUHqvBzZXWKPyDugBXTORXRFBSUWiaJ8iWArVBaJKqGq/FYJK7FGHLvUlAWjWn1dohzbGo11m9Mukb1NFe/M9ap0H9gikQ0S4fU6a9Gc8xLdVlXetPk6QUidX7LgsE4raD5ci+biBsq7nDIZNk7U81l8VCcCztekfheJ56QvJY5zM+VFPucO6HiLjtfgU1z9n31alWHLsuoCfwPOtW0717Ksl4DbgddP537PKCZM0GKt6Gi4/XYYMACCaUHK/v2qqj71lETYqFFKM1i7VsImGJg/X8fev3/Jdf37K6YsWKLW1qzR8136BKR+fYiJ0WsR6BQUwObNyhc+EUdmN0lJ0Lu3b4/LYAg0bFvWhZVvQ/IEica4ASU2iCO7Iekr+OVWCb4qYdDyYgmyFhcpmzdlim7fNlOCM7wmNBsEPf8C8UNUSd75m2wWsx/Wz872yc6kha73Koqs3jmySBzeKdF4IEU+4k0/6OfsbWVnAYdGqiJctbaaY0TVL8kXDgkvuVghEsTFhaoK20USmQXOqvAh2S8KDqoyXFYSRXh1qBkPtZuralu7pSqyMR30+FkbYd86x+K5ZTrBWPGm/rZqLXmm486D7g/CxZ9rTFunwdapqhqveLPUicZIuPgzddDb/DMkj9drtey/qkQn3gA9H4GBL8nLveo9mPcYzH8SWo+A7vfrJCRYiklnCaelAmzb3m9ZVn/btp3vzlCgcjMss7PlWY2JCZ7FTqV55RVo21ZRXq1bwwcfyGoQLMydq3/OzsSCiy/Wdvbs4BHDq1apKlm66tirlxbRbdwI7dv779hcwbYleE+cVbAsLUBzLkwLZLZvl6WjZcuTb2vVStvNm40YNpy9FBdJYP7+Euz6XQK2811wzl2qXqb8CN+PkEjD1nT+sHeV/lBcqOiw8cOVt4stUdjlzxJgjfuqSrptJsx6EFLnqUqLBbGJyt5t3Ef71YhTZXjvKlkvVr4j8VtwqORYw6urOhx7ju6/emNZDKo3ghqNVC0N9ULcqG3rOI7sgZw92h5KU4vobMdlxxwJaScRdSRSYxNlAelwg6wTB7Yoci1tgSrCm3/S/mHVJI5bXAjnv6rYtrQF8htv/B6m/gzT7oKm50GbUTDkbRgeLlG87gsJ33mP66Sjy5/h2plK3lj1vvzHyeNl2+jxF2g7UtVwg9857VfBtu08y7IigH8DVYGPS99+2hE9WVmQkQFHjgRfikFhIfz+u6aBW7RQg4Gvvw4uMTx7tjyePXro98aNFYG1aJEaPgQDq1eXHL8TZ6LBmjWBL4Z37FASRlknH5066QSruDiwTxY3b9a2LDHcvLmEvXMfg+Fs4miOKpVLX5VAq90ChrwJiTdrIdrqD7XA7fBOic2+T0CnWyAiWuJ5yhhN2dtFENsJ+j+jyK+6bWD7HFj/NUy5riRFom6CpuybDdaCr/wDEtA7F6vCuWdVSdxY1dpqxJF4k+47pp1EcFQ9/1Q2LQuq1tSlbuuy97FtieTMJC2ay/hDl/XjVKUFh12ii9I24ofAuY7v5NT5OlFwnjTMelCvR4sLVXUf8H+63+TvdJlxD8y8X57sDjfCNTPgyC4lUqz+ECZeoROFc+5QVf7c52DdZ7DsNZh8jSr03R+ETrfpBMPgN05bDFuW1QT4AHjdtu1fTrz9tCN6mjXTNPbu3UoyiIw83UP2HbmOIvkVV2h7ySVaxLVli8RxMLB0qYRkeHjJdX37Kqs3GLqGZWcr3/b224+/PiFB76s1a8qeug8kNmzQtixvfUIC5OTAzp3QJIBjfU4lhiMidJJlxLDhbKLgMKx4C5a8JG9pw14w8D+qtO5eLptD8gT9n20xHIa+LTvErqWw4BlI/lZCumYzRam1H6M83ZTJsPBZ2DZNjxFWTb7XVpdIAFcJVfV0849qKpG9TccTFgUNeki0NeylCLIaTQL/f/yJWJYacFRvIF+0E9vWycaupaoI71qqk4zlDldn3QRVe+MG6oTj6BHZJLb84rBVvKVqfevLoO2V0Ocfur/1Y1URnjJatydcpcV6ff+pavPKd2HhM7DoOXm5e/4Vbt8gK8vSVyS4Fz6r67veC1WDIBnoDOR0PcMRwKfALbZtp1bKEZ38IPJG7tmjCnFcnFcexivk50OjRpqiB1WGAWbMkO820CkslFj885+Pv75XL1W4nQu4AhmnhaBz5+OvDw+XuAwGi8GphKTTYpCSEvhiODJSJ7Rl0bKlEcOGs4OCI6rA/v4feWCbD4e+/5BFIWUKfD1Ii7mq1tJUete79fMfX8InXWRZCK8O7a+HxBu1CGzbdCUdpEyWQK7eUOK41eUSeHtW6r6XvKK/B1V9mw3SYzTpLxvBmTxlb1lQp6Uu7R0FkOJCNeBInQs75mnR26r3UJRaD1WD+z4Bl43TCUTyd6rG//GlXoOWlyhKrd9TiqZb9zlsGAdrPoKYRL12l38Luft0v6ve1wlOk3Mlfq+bBzuXSCj/+jgseVknI13vVfXb4DNO950/GGgHfFGqBehs27afPc37PZ6wMOWoZmcHnxju27fkzLpNGyUYLF4cHGJ40ybIyztZSDqn69etC3wxnOTIzXQu0ipNYqLsHoHO5s2qnpb1XJcWwwMH+vSw3GLzZs2GlFdlatlSvnqD4UylMA9WvA2//1uxYPFDFY3WsAf88ZUiufZvVKX3/Nc0dX4oFRb/nzKFC/O07/APtFhuf7Km4r+7VKkNkdGaqnfGo22dJmH2040S3VVCtRCvw7/Uma1+FyU4nM1UCYVGPXXp9TeJ4z0r9dxt/kkV3YVPKyqu5aWq+g55Qwsckyfosv4beaTbj4EeD8nisv4bnfBMvxvm/k0nLl3vgT7/1IK8pa/B95eXNEgZ+YMed9Gz8Os/dNLS6xFlPIcF0Wx4EHO6C+h+BHzTi7BWLUhNlcCsWtUnD3laFBSoslq69axlQffusHy5/47LHVat0vZEMewUlmvXllS7A5WUFL1fyqqatmkD33wT+O8pp5AsyxMcF6eTxZQU3x+XO2zeXHZl20nLlpppOHLk5BxigyGYsYvlV533mLqkxQ+Bfk9LgP3xJfx4AxzYLHF62TdKK0idJ0/pll/kb+1wgxZj1W6h6uXYARJPoRHav/0YpSHsmKPqY8okWSQi6qi62epSWS1MI4hTUyVUJxwNe8jmkJNRIoyTx0vIRtSRlaXtVTDoFdg+E9Z+KrvF0lf0Onb+E1z3q7zKK9/WwrlV78p73PMRuCsFNkyQReaX22DxCxLKTlG84Gm9X1a8pRSRDtebExcvE8Arbk7AmQRw6NCp96tEcnNzOe+88ygqUu/1tLQ0xo0bB6jhxoABAygsLCz7j3McUcsnNnXo1k3VSuftgczq1RJaCQnHXx8bK+tKMHQNS0mR0CpLSLZuLR/Z1q2+Py53OJWQDAmRUA5kMWzb8smfSgzHx2ub6h23lcHgF1J/hS96awFbZF24dhZc9Yuivj5IgJ9v0XT4yElw4xIJ58+6w7ghigE79zn4cyp0u19V5bcaqdpYXKQK5D27NKW+6Qd4J05V4i0/Q7vRcM1MuG8vXPoltLvGCGFPiIqBDmPgsrF6LkdOkjUi+TuYcBG811zxdP2fhnt2wuA39BpOuwvebqwTl96Pwd1pMOAFecG/OR++6CNxe+PvMGqKBPYvt+o9kZEEoybB6DmqOP98M3zWTXnRBq8RPGI4IkKCxoci8uOPP2bkyJHHOs/NmjWLFSvU2jI8PJwLLrjgmDg+CefiuROn57t318p/Z9U1kNm4UdPwpRfPOenYMTjybVNSSqwEJ+K8ftMm3x2Pu7giJFu1CmwxnJmpz8Op0mSclXsjhg1nAge2wvdXwNjz1Azj4s/hpmWyOnxyjkME14JRkyWCCw7CR4kSzcWFcNEn8KdtsjtMuQ4+7qhGDu1Gww2/S1QXFcCX/eDLvhJdLS6CK3+Ee3fD8Pch/oIz2wPsa0IjtHjuks8ljEdNVjV+5dvwSWedwNjFcO1sGLNAix1Xvg0fJsCka+Xt/tM2GPaeMp0nXQ0ftpPF5YbfdH9Va0r8fpSotts3/g6Xfq39vx0G4y9STJuh0gmoT8qDD55KI1qQkwDYEOX6fXburAZdp2L58uX89a9/Zc6cOQCsW7eOO+64A8uyGDt2LAALFizg4Ycfpnbt2kybNo2JEycyYsQIHnvsMcaMGXPynebmqmp3Yketjh21TUo63kIRiGzaVL6QbNcOPv00sBMliotVVR06tOzbS/ttA5Xdu3UCeCox3Lx5YLczTnd0czrVAj/nWgAjhg3BTGG+psoXPa8WvOc+Lx9p5gb4ZrBsDHVawYgJij/74yv4sL06psV2hMvHy9KQ9JUWy+3foMVwA16Ac+6UT3jpq8q7LT4KjXrD8A8h4WqTQuBLQqvqdWp1qZJAkr6WFWLWAzDvUWh3nRbInf+qfN0r35KYrd8Fev4NblunBY2LnpOne/ELss7cuFTXz/u7PMVNB8Kgl5U+seJNeZg/SoRej0Lvvxs/cSUSPJVhgJAqUFTMcT3IK4F27dqxcePGY78/+eSTPPPMM2zZsoV4x/Rt//796dGjB5MmTWLVqlU0b96cxMREli5dWvad5uWVXVFt2lRVbmdcVqBSXCyR2LqcLMeWLWVZycjw7XG5w65dOikpT9BHR0OdOoFdGd6yRdtTieG4OC0uPXjQN8fkLmlp2p5KDDdqdPy+BkOwsW0mfNJJC6BaXiwB0+lWTZl/1g32rdU0+m1/qAvbx+eoChhWDa74XhXi3Az4oK18pKERcMkXcMdGqNkUxl8IX/WXh7XrPXDrWrhhMZxzmxHC/iQyGrrdq8r/LauUybzhG/i0K0wcqa54d2yECz9S0seU0bJD5OxVRXjEBFXwp4zWrAG2Xtshb6lr3mfdYertOuG5fQO0HaWFdh91UCMWQ6UQUJXhiiq4ZB6Rv7NDh0rNG46KiiIiIoIDBw6wZcsWsrKySExMpHbt2sftl5ycTNu2bY/9HhISQnh4OIcOHaJGjVL/jGxbIiws7OQHCwnRwq1AF8Pp6RL05Ynh0l3DYmN9d1zu4Kz4lieGnbcFcmXYWSlt1qz8fZz2g9RUfTYCDVfEcNWq8qGbyrAh2MjJUEUwaazaAF/1i1oBL38TFjwpO0Pvx6D3o6oQjxsiL3Gd1hJCLS5S3u17reBwuqq9Q99W1NrKt+H91mrBXDdB13e4EcLNItOApN456gp43r+0qG7lW2qKUiNOleIbl8L2WUoUmX43/PYvRbfdtFy+7wVPS0DHDdDivLtS4Ld/q0nHxomKcLvoU+h0uxp+fHepFlAOeUu5ygaPCa7KcISjvWNeGb3JT5P27duzYcMGnnjiCZ5//nkiIyPJK/U4mZmZ1KpVi7ATBG5+fj4RzuMquVKCuCwxDLIYBLoYdlZLT1UZhsAWks5jO1VVtVkzdXgLVFwRkoFuMUhPl9+/vIxhJ02amMqwIbhI/l4Vug3jJVRuW6dK76dd1dCiSX9d1+XPMPVOLabL3CBRe+taNXb4MEFdzOq0VAezUVPUEe7deFWZ650jgX37H7ofI4QDn4ja0ONBuCNZPu5azXTC9F5z2LdG1109TQvkpt6h91BRgSrLw96FzPXweQ+Yca9e89vXKw5v7t/gU0ck3i2r4LwXlXTxUQdZbuzKnTU/mwhOMexcnFaJdOjQgU8++QTbtunXrx916tShqKjomCDeunUrjZxTuQ4yMzOJjY09SSCTn69teWI4IUEVbi+I+kqjIjEcDC10d+zQMZ4qm7ppU4nIQP0nkpYG1auf7D0vTaCL4bQ0CeHQCiai4uICdwwGQ2lyMmDyaPhhlLq03bQMuj+gat/YAVrwdMVEXTaMl+BNmQJ9n4Q7U5Ql/HkP+OkmZdheM1N+4a3TJIIXP69ucTevgKunKhbNCq6vawN6zVpeDGPm69KoDyx4Ct5pptbPV0/TyU94DXmHP+sOtZrrPdL7Mb13PmijZh6Xf6s0i4LDWpg59Q5ViG9ZpdbbP14vn/Ghnf4edVASXJ+ukBD5cL0gIjt06MAHH3zAc889d+y6oUOHssCxMCkhIYGMjAwSExNZ5GjUMGeGpUPTAAAgAElEQVTOHC666KKT78wphsv78m/btsSTG6icKp8XdFtcXGCPITVVIqy8kxKQGM7Jgf37fXdc7pCWVnFnuUaNVHkN1Aq3K2MAUxk2BAebJqsSl/ydos9u+E35wR91kGjp9SjclqT2xp90Umex5sNU3Ws7Cr6/DCZcLP/oZeOUDJH6K7zXQovjWo+AW9fBFRO04MpwZtCkP1w5BW5dI2vM4ufh3ebykl/3q8RuYY4W2k0erWzpO5Kh1WUS0J900qzD7UlqBZ30td5zGUlKrxj0CmyboevWf+vv0QYdwSWGQV5hL4jhG264geLiYrp163bsunvvvZfPPvsMgOrVq7NkyRLWrVtHX0cKxNixY7nzzjtPvrP8fFUkQ8oJyW7RQttt2ypzCJXL1q3Kfi0rn9dJoLfQTUuruGOh8/ZgFpKhoRLEgVpVTU93TQw7FwL6MEvcYHCZwjyYcZ+qb9UbqRrc5c+KSfvuMoiMURRWj4e1AO7bYYrauuoXuPBjCd1Pu0r8DHlTFb3DO+UVXvSsBNLt65ULHBuA3n9D5RDbEUZ8CzevlED+9XF4vxUc2QO3rIGBL0HaAsXpLXkJhr6jCnJxEYwbDL/crmzpm5ZpVuKHUaoKJ96ov49OUMOWn29TFdngEsEnhiMiJIZ9MK3dpUsXBg0adKzpRmkKCgoYMWLEcQvqjlFRRzNng4FAbvaQmnrqXFgIfL9tamrFYtg5xkAdh6tV1UC2GKSlQWMXGlU6x2mqw4ZAI2M9fN5L8VbdH1I1+FCawy88Tn7hm5Yp+uyj9rBpIvR/VuLk8C5Nda94EzrfpWSBag0ldmY/JE/wjUslkOq28fdIDb6ifmdViq9fBDHtYeZ9ss7EJmrhXOc7YeU7stjk7JXHvN9TsPE7Xbdnpd6H5z6nWYqPOkDGOlWZ+/wD1n6ik6/dQdLx1s8EnxiuWlUWg/I6v1Uyt95667GmG6UJDw/nxhtvLPuPKhLD9eqpwh3IlWFXhGRcnOLLfPRauIVtawwVCcnSSQyBRmGhnt9gFsOHDinyzZUxOBfY7dnj3WMyGFzFtmH1R4pGO7ILrvxJi5bmPiqrQ1Q9Cdlz7oAfrlRyQO1WqvolXA3fDlVnsTqtJZa73qNmCz+Mkk/06ulw7Uxo2N3fIzX4i8Z91Khj5CRlR4+/UF7yrvcpZaJWc7Xs/u5SaH+dRHFsR8XyTRwJnW6Dm5erSjxxpER1n8fVwa4wV93ulrwauOtiAoTgFMNQ4ssNNGy7YjFsWaoOB2pluKBAzR5cEcPFxbAzAA372dlw5EjFY4iN1WsViJXh3bv1/Lrjtw20f3iuNNxw4hTDu3d773gMBlcpzNOU9NTbFXN2y2oJky96wfL/Qbf7lA28P1mNELbNlG/zunmQMlmZsRl/yCJx5U/yE3/cSZW6wW9ocVzzIf4epSEQsCx1t7vtD72H0hfJI7z+G3nKh74Nu5dpNmH9OC24PP812D5TFeG9a5Q53etRWPUefN5T+ce3rNYCvjl/gUnXGNvEKQgIMWy78wXubGQRqGK4qAiKi7HLarhRmubNA7cynJ4uUeWq3zYQK5LOY6poDM60iUAUw67Eqjlp2FApK4HWeGPXLm0bNqx4XyOGDYHCwVSlQqz9WFPOV0+DLb+oQnwoXQkA574A0/4Ek6+VT/PWNdDsfPiyD8x7TN3JbkuSKPmoAyz7H5xzO9y5SU0aTKtkw4mEhEPPh/Ue6XCD8og/7qSTsNs3QOsrlF39VT+IHwI3r4K6beUZ/vEG6POYZhtyM2W5WP8NXPEdDPy37BWf94LMZH+PMiDxuxiOiIggMzPTdUEc6JXh/HxsILOs/OHSBHJl2FUheSaIYec+Z4IYhsATkk7LQ/36Fe9bp46SP4xNwuBPdsyV6M3coGi0vk/A9D9rUVzjvhK9UfWU9/rHF7p99Fz5Nj/vIY/wiO+0SG7WA1pw51xcN+xdiIrx9wgNgU5ULFz0sd5XIVVlnZj9EAz+nxq1ZG+Hz7pqBuK6eWrXnfydWnhXramKcNNBaswx5Xroco9Ecs5evUc3/uDvEQYcfj81bdKkCWlpaezbt8/1P8rK0iK67GzvHZinHDkCe/cSERZGk/bty98vPh4OHNDlhE53fscpJCtaQBfIYtgdIdmoESxc6N3j8QTnGFxZfFa6qlrWok5/4Y4YtiztF2iC3nD2sPIdJUbUaQ0jJyrKauy5sGupcl/PfVYV3nl/V6LE6LlQK17JEanzoO1VErybf4IP26mpxrnPQ6+/QcgpIh4NhrJoep5SR37/Dyx+QVacYe/KTjH9T2rCsekHuPQriBsIU65Ty+4B/6fZiyUvwbzHZde54nt5i3+4EiZeIQHd+zH93zX4XwyHhYXRvHlz9/7ojjsUJzV3rleO6bR47TV4+GHIzDx1vq0zUWL79sAVwxVVVWvW1CUQxXBqqmLhXJmeb9hQ0/m2HVj/GHbt0nsoOrrifZ1i2GlLCBT27NFntU4d1/Zv0MCIYYP3ydqsFrcX/Fd2BbsY5vwNlr4ij+WlY+XtnXyNvMNXfK8mGJNHQ/IEtcC98CPYOl2xanah2uS2ugSm3aV9GveDCz+UhcJg8JTQqtDvCWh7pRpz/HAltB+j91+bkTD9HlWEL/wIblkJv9whkbxjrmL66neVleez7nDZ10qb+OU2dTfMSpG4DqnA1nkW4HebhEe0aAFbtvj7KMomPV1JERV9+Turfc4FRoFEaqqOv5oLbT8DNcUgLU0it6KuZ6D98vNVpQ8k9uxRpdQVgR6oNom9e7VI8VR51aUxYtjgbfauhi/7yk95YKuaX/xwpYRw13u1qn/9NzBuiMPesATqJmhR0sbvYeB/VIn79XGJ5bpt5d2s3kj+zk2T4Lx/afraCGFDZRHTTjFs/Z5WnN9HibLr3LIS6rRSQsn8JyWAh7ylBhyf9XBkYi9XS+jxF8Hy1+GSLxXTtvYT+HY45GX5e3R+JzjFcLNmSjAIxEgvZ6ZqRQImkMXwjh2ueW0hcMXw7t2uVYWhZL9ArKq6Yi8AnbyEhwf3GMDYJAzeJf03GDtQlbAxC+Sv/HqQPJTnvyZP5ry/q7obP0Q5rhlJ8EVPyNuvVfwJV2tx3cp3oOcjMHo2rHhLMWpVa+lvej8KVcppumQweEpIGPR/Su+xqrVlz1n9oU68ejysLOsv+qh99+g5sul80Rv2rJCQTrhasYDT/qSFoRd/rgYfX/TRieFZTHCK4SZNlNoQiAtt0tNd83g6BVggimFXOrc5CWQx7LQOVMSZIIYty29V1RkzICEBLrmkjK7W7orhBg1g3z59vg2GymT7HHXwioyGMfMhNFL+yn1rZYPofKcqxEtehi53qyHCyrdVcYvuoOpaUYEaGWQm62+63Qtfny/LRdd7lCXcoKu/R2o402nQDW5aCp1uh99elCju/pB8wge3yxJxNEfv2diOel8vfkEzGn0eh9Xvw4RLoPXlyrnO2auEin1/+HtkfiN4xTAEZqcqV1vPhodLJASiGN61S4vKXKFhQ4mXQKvSuyPC/GwxKDdIxRMh6eMx7NkDI0cq1W36dLj77jJ2cHcMRUXy3BsMlcXmn2DCRVrsNmY+FObDV+dCzj5Ve5v0h68HllSIL3gNpt6piLR216rKtv5rreqv0ViiNzTKIYyT4PLxSo8Ii/L3SA1nC2FRcOEHErh7V8GnncEK0XuzemMYP1zv2dFzJZoX/5+awvR9AoZ/CNtn6WSwVnP5iEEzHjuX+HVY/sKI4crEtl2vDIP2CzQxXFQkcetqVbVBA43bnTQQb1NUJK9qEFSGn3pKHcYvvhhyckrdUFysMbgrJH08hpdflhCeMQMefRTGjYOkJMeNtu3ZGMBYJQyVx6bJ8P0IiOkgYXBkjxIiivL1e82mEsb71ipBIvFGVdrWfgJ9n9TCuBn3alFS2ys13Zw0VsK4eiOJj4Qr/TxIw1lL++tUAa7RRF0R14/Te7T1FTDnr+qAOPh1ZQ1vGCcvfJsRcNUvimj7sh9UCXPYhmrBuAtg+2x/j8rnBKcYdorNQBPDGRnq3uZKZRgCUwzv3Ssh5qrf1o8pBkVF6ltyUmU1M1M3uiqGa9SAqCifj+Hnn+HZZ6FnT/385JOlbszKUrXdHSHZsKFPRWRREXz5JVx2GbRpAw88oPWKn33m2OHQIUUg1qvn+p0aMWyoTLZMhUlXaUX9tbMga5MqwCERqhCHVVN17HA6XDUVGnSXME5fBJd8Ad3vdwjjjx3C+GO1yl34NCTeIO9m3Tb+HqXhbKduGwngdtdqYefUO+DiTxXrl/Q1fHMBdLwVLhunmMAv+0LtFvIaF+Xp5DD/oARxzXid6KX86O9R+ZTgFMPR0Wq+EWhC0nk8wVwZdooQd6uqPhYv2dnQu7ca+V10ERw9WupGd7JtQX5bZ7yaD3n6aQWjzJoFN90E77xTyh3g7higxG973JPhPebN08s+erR+j4mBIUPg228dJyiejMG5rxHDhtNl+2zlqcZ0gKunyuf77XA1NLh+ARTmSgQcPaIKcfWGqpIdSlXHuUa9tfho52Ktvj/nDk0jb/oBzn9VFWNjizAECmFRskwM/Dds+FYndR2uhxHjYe9KdUZs0NXhEc7Q75YF183XyeHXAyF7mwRybCd55Tf/4u9R+YzgFMOWpeproFWG3WmS4NwvM1PVMx+TkgI//aRC9nG4K4b9VMl74glYsQLuvBOmToX//rfUje6OwbmvD8Xwhg2wdCnce6/s4w8/LJvEuHGOHTwRks4TEx8tLJ06Vcd+8cUl140YoWp9cjKejSE2VtuMjMo6TMPZSNoC+O5SqN1KnbcObFWFNyoGrp0jMTB2oGN6eL6+U77q7xDGczRd/GU/RU5dO0dNOD7voVzWUZOhx0OBlUluMIDek73+Blf+CNlb4Yte8slfM0vv5S/66D1//SJ1ths7UNdfv0Axbd8OgT0r4ZrpOomceAVsmebvUfmE4BTDEJhi2FnldccmAYqJ8yFz50Jiolb/X3rpCQv33RWSfqjk7d8P770Ht96q7bBh8NJLpYS9J2LYx5Xhb75R9O611+r3Tp2gXTsYP96xg1NIujMGpx1h795KO85TMXcu9Oolh4mT88/Xds6cUsfhjhiuVUteCyOG3cayrCsty/rWsqwye4tblnW1ZVlLLMtablnWK74+Pp+xZ5XyVGvEqQp2eKd8klVrwbWzITdDqRJVa0oI52Y64tYiNE1ccNjxe1X9np+lqlloJFy/WE05DIZApuVFeq+GRMDY8yA/WwLYGSV4YIve+5HR+ixkpej32i11Erl3NVwzQznZE0eo890ZTvCK4caN/SKGjx6FN9+EF1+UJfI40tKkcFz98vdD1nBhIdx+uxLRnn9eCQCfflpqB6eQdHUMkZESMD4Ukl9/LeF7zz36/b775A6Y5jyBdXcM4HO/7dSpEpKlrdkjRsD8+Y731elUVX2wmDE7G5Yvh0GDjr++ZUudC86ZQ8kY3PEMW5b8FoG0IDN42AfcDZzUTsqyrGbAc8AQoDvQxLKsUb49PB+QvU1+x6q15RHOy5JfMixKecD52fryD6sua8ShdK26r94Arl8I+zeoglyjsX7ftQS+uxxi2ssfHNvB3yM0GFwjph3csFh+4u8u1WzJ9YslcL+/XBXgMfNVOR5/Eexeps9MreaKXctcr6SVOq3VZTFtgb9H5FWCVww3aSIRWW4ulXe4/36Jr8cfh8sv11qzY+zcKfHiStcz8EtleMoU2LwZ/vMfjaFrV1VVjz2Nu3apxXKUG144HwvJb7+Fjh2hc2f9PnQo1K17gsUgMlIL41ylQQMpPB9YVg4dgmXLSqqoTs4/X1X6BQtwv40x+FQML16s9/555x1/vWXBgAGwaBEag2WVHJerxMSYyrAH2LY9z7bt8p644cB3tm1n27ZtA+8BI3x3dD4gN1Oe4MI8eYRBwrZKiCrCR3MljEMiZIU4vMshhBvJCpG+GCaOgnqdJRLWf6PFck0H6vZqbpzUGQyBQPWGMHoeNLtALZhXf6DPQoPu8MNV8tVfNw9iE2HiSNi9QoK4RhMJ5KwU/V6zKUy4FPat8/eIvEZwi+GCAp9WkFatgnffhQcf1HbOHJgwodQOnnTbcv6dj/joIz11l14qnXLvvfJ3Ll/u2MGdzm1OfJhve/iwhNhFF5VcFxYGw4cr3su2KWm44Y6nz1m99MH7af58id4Tq6p9+2osx6qq9eq53sYYfCqGne+X7t1Pvq1bN52n7tmao8Wurp4cOjFi2BtEA6U/pLuActWdZVl3Wpa1zLKsZfuCoUp/NFfVq+xt8vRWb6QKcV6WIqRCwlQRDgmTEM7ZJyFcraGEbtp8mHIdNO6j6eElLytKLeEauPInqOrGibXBEEhUrSEPcYfrYf4/YclLWiAaNwB+vAGSv3dYItrLEpG5XoK5Wn2dTB5K0/5hkTrZPFimCyvoCV4x7IcUg9dfV7HxqadkNWjbVtcdw10xXLcuhIT4TAwfOQIzZ8JVV5Xok8sv18/HvKrudG5z4sPFZ/PmyaoyZMjx1w8eLIvqunVoDO68DlAiJH3gt50/X895377HXx8VBT16wMKFuP9eAqhdW+8nHwjJlStliahZ8+TbunXTdsXmWu5ZJJzExhqbROWzh+PFbwPHdWVi2/b7tm13t227e6y7lX1fYxfDTzeqsnvJl9Cwpxb+ZG5Ql7gaTfSlXpgHV8+Ao4f1e7X6EsZp89WMoHFfuPJnWPQs/PYv6PwnuGwshFb19wgNhtMjJAwu/gzOuVPNNxY8JYHcYjhMu1PNZq6Z4fAMXwLZWySII2rrpNIuVvTg0cMwbphmYc4wglcMOwWbj4Rkbq6qwKNGlWiOW26RcNm8mZJjcUdIVqkiseCjMcyZA/n5x1dV69bVtPZxflt3xbAPbRKzZqlJRb9+x19/wQXaHququjsGH1ZVV6zQAsbIyJNv69FDMxBFu/e5L4arVPGZ33blSujSpezbnNcvT2+gyrC7mMqwN/gZuMKyLGeJ81Zgkh+Pp/JY9DwkT4BBL0HbkRLGO+bqy79RbzUiOLhDX/6hVVXdiqjtsEYsKiWEf5JIWPIydL0Xhr4NVvB+RRoMx2FVgWHvQrf71T58zl9hxHcQP1QWim0zHBaJOFkkjuyRAC4q0Mlj9YaadcneKstEoe9TsLxJ8H7SfZxiMGOGvJ7XXVdynTMJYMoUND/vSTWvfn2fjWHaNKhWDc499/jrBw2C1asdGbeeVoaPHJGHwcssWaLKY0TE8dc3bSoL9u+/49kYfGSTsG2J4a5dy769WzdFrG1Ir+H+ewl8UlXNzoYtW8oXwzVrqgnHiv3NJGzdJTZWkSHHxZwYPMGyrG8sy+ps2/Yu4P+AXy3L+h3YY9v2d34+vNNn4w8SsIk3Qo+HYeGzylgd+B91i/vhSti9XM0GarfQl7pdrLi1zCSHEO4jITz/CYmEbg+oY5eJTjOcaVgWXPBf6PUorHxHVqCREyHuXFkm0hdJEEdGq315SDiM+lHZ2xMugfrdlGW8c7Eae/h4zZY3CV4x7ON821mzVMkbMKDkumbNICFByQBkZ8vD7IkY9lFlePFiJRhUPWHWz+ld/XV6nhS/J2IYvG6VKCxURbIsnyqoqrp0ia2qYoDaJNLSdHinEsMAyzPjA9ZisGqVtuWJYVDlO+lIvOeVYduWIDa4jW3bDUr9fK1t26scP39l23YX27Z72bb9V/8dYSWxbx38dAM07AHD3lN1eOEz0PEW6PlXmHkfbJ0GQ9+FpudpuvfIHrjqZ8g/4GjI0R5GTYHfXoTl/4PuD8IFrxkhbDhzsSw470Xo+QiseFMnkKN+1KK6Sdfoc3XVVJ00jh8OdVvDZd8obWLyNdB6BJz7HPzxJfz+H3+PptIIXjFcvbpMlj4SkrNmQf/+JwvJYcPkY83b4UGmqnN/H4whJ0fV3969T76tRw9VWufPcEx7uCuGnWP2spDcsEHjOJUY3pRikUVt94VkzZpaveZlIblypbblieG2bSEqymbF0UTPhKQPxPAff2jbsWP5+7RLsEkpiqegjgfVbWc12VglDOWRu1/xUOE14IqJWvTz003QqA8MfQdWvg2r3lMFrOPNWimfkSQPcVg1TQNXa6gv/dUfSgx3vkud5YwQNpzpWJY61XX5M/z+b50IXj1VJ4eTrlTzmVFTtHhuwiXQbDAMeRM2/wTzHoM+/1Dr53mPwabJ/h5NpRC8YtiyfGYx2LNHAsDpSy3NeecpjWvlgiO6wl0x3KCBHsDL0w3Ll6uy2qfPybeFhyumbPlKq+SY3MFHfttly7Q9lRgGWEZ39+O8LEsC2stjWLFCD9WpU9m3h4RAh9YF/EEHzy0GXh5DcrLsNqdqtNi+RR5FhLKpuKX7D+BD/7YhCLFt+PkWOJgKI75XR63vLtfU7hXfa0HczAeg1aUw4AVViLfPhuEfqKvWt8M0/XvNdNjyM8x9BBKuhiFvGSFsOHuwLAncDjfIIrTuMy0gjagrn331hqUqwtdq8V2Xu5VG8ccXcOHH0KAb/DjmjIhcC14xDD6L9Fq8WNvSFgknzkrrb787/ol6UhkuKJDNwov89pu2vXqVfXvXrrAyOYpiLM8tBj4Qw9Wry49aFs5p+zV08lxIerm6nZQELVpITJZHuyaHSaK952PIylLkhpdITtZrcCrd0K6+LA5JOfHuP4CpDBtOxfLXIWWyfMENeygSLXcfjPwBCg4pPzW6HVzy1fEV4rZXKn4t/4CqYHvXyPcYPxQu+UJ5xAbD2YRVBS76GNpcAbMekhf4yp+1OO7bC6HJuTD4Ddj8o2LZLvgvNB2kz83e1frMhVWTNz//xC5kwUXwi2EfWAyWL1fFztnkoTQNG8o7/Ntah7rxRAyD18exYoWOs7yCabducCg3jBRauS/CfCSG163T1Hx50bsxMVCvVp6qqp7EQfmoqpqQcOp92jfYz04ak13VQ88wOFZDeofkZNk5TkXb2nuwKGZ9tpuZ1VAyBiOGDSeyaxnMeQRaXQbdH4DFL8D2WTD4TQngiVdI1I6aDOkLYdaD0PpyGPC8Uib2rIRLv4aioxLRDbqrmhxyUtM+g+HsoEqoThwb9YYfr1eXxpE/KF5t4hVwzu2yEP32L/nyR4yH6o11G5Y+T1mbYNpdQb2gLrjFsI9sEsuXQ/v2ZUdhgarDv22OlUpz1+fpIzHsFJLlcWzhFt3cF8MRESrZellIJiXpdTgVHepnBqzFoKgINm6sWAy3q62FiOsPnIaQ9NI4cnNh+/aKxxB1ZB/xbGP9Xg98z87PkLFJGEqTn60FPNUawEWfKD5twdNqJtDpVph+j3zBl34N2Jraje2o7OH5T8LG7+H8V9Rh7vvLIKqeRHP4KaZpDIazgbBIfRZqNNFno3ojfcZSf9UJ5eDXoUl/RbBlb9e+BQd1Qhl3LvR/FtZ/Davf9/dIPCa4xXCDBqoeeXFK2LY1Pe8Ui2XRtSvsOFibrOhWKiG7gw/EcEGBFp8lJpa/T/v2EFalkNVh3ctX/afCy0IyM1N3367dqffrUDudJNpj1/VAhNWr51WbxI4d8pdXWBmO2gbgmZD0clV10yZ9JiqqDJORQVuSSd7pQecu58mVqQwbSjP9Hn0RX/Y1FDsqu3XbasHc2k9h3afQ9wl9Of9wpaaAr5gIKY60iHPuhE63q6lAwWHlDlfzYIGnwXAmEhWjbo1YilVrcSH0+psi2NZ+pkziyBj4foQ+N0PfgdR5sOAZ6PMYNB8GM+9XS+cgJPjFMHhVhKWl6e5PJYadFde1NfqWv1N5+EAMb9yoxXOnqgyHhUHrGrtZH1rOyq6K8LIYXr9e2wrFcNRWDlODHbvC3H+Q2FhlJed5J0w8OVnbioRkc3sLVckjabsHFSsvV4ZdHQOZmbRkM1vSwj2bOTNd6AylSf4ekr6Cvv9Ug4yfblaleMR4NQGYcTc0Ox/6PanFc3tWwsWfQ2EuTL1dVa0hbyiKbd86uHw8xJ6iOmAwnI3UaeWwSGyHydcpQq35MJhxD2Sl6LacvUpu6XA9dLxVVqVtMzUDE1UPpoyGozn+HonbBLcY9kHjDWemanlRWFCSDLA2/BQ7lUd0tOwVXhTDa9dqeyoxDNA+YivriytSOeXgIzFcoU0iZANQEv/lFl4Wkht0aBVWhkOyMmgdsoXkTR58PH0khstbxHiMjAxasJXsg1XIyvLggUwXOoOTnH0w/U9Qv4sinVa/D1unwqCX1T72h6uham24dCwkjdXtvf8OcefBxFGKX7tsHCx5BTZNklWixTB/j8pgCEya9NOJ49apsiFd9jXUagY/jJJ94vxXYcsv+jwNeUMJLVPGQFG+uj7u3whzH/X3KNwmuMWwD1oyuyLCGjWCOlUOsKawg/sPEBIiAePFMaxbB6GhFVfz2lXZwOb8xp4VRr0shpOSFCvdtOmp92tfuAYoEZ5u4cwm9pJVYsMGtb+u0M6ckUHLiJ1s2eLBg0RHK+bBS6/Fli1aNHqqNAwAMjNpUWPvsb9xGx+1lTYEOLYN0/6sKvDFn6mt8uy/QPwQZaTO+zvs36A0iPxsiea481TRmno7ZG1UPFTmeq2Gbzda7WgNBkP5dL4LzrlD9qJts2Q3ys9Wl7rOdymZ5dfHlSgxYjwU5sDPtyppovuDauaxdYa/R+EWZ4YY9mJlOClJX/61a5e/j4VNR9ay9kgLzx7Ey4031q1TJS+8ggXT7QtWU0wImzZ58CBOMeyl1aTr10vMl5ck4aRu9lZqhx1m82YPHsQHVdW2bV2IMs3IoGXNfWzZ4sHTGRIixe2lMWzdCs2bu7BjRgYt6x4A8Oy1iI7Gs5JyxWzdqkaLhiBg/TjY+B30fwai28PPN2v1+4UfKUVi+evQ7T4J4B+vh5AIVYhXf6C2zANeUPV48rVQNwGGv2+yhA0GVxj8hhImfr5ZWd6DX4ftM9WkY/gHUCNOn6tq9VwP/DYAACAASURBVDVLs206rHoXBvyfkl1+vgXyvPM/3BsEtxj2gU1i/fqKfaocPkyn4lWszWzkuT/Si1PCriQYALQ/vATQCYDbxMZCfr48t17AlUgyACtjH61q7iMlxYMH8bIY3rIFWrrSgyIzkxbR2eTmetjhOjraa62Mt22D+HgXdszMpHmDXMDDynDdul4bw4ABcN99XrlrQ2WSlwWzHoCGPdVeedl/IW2BvpTDa+jLtm5bOO9f8i3uWqq2zAUHYfbD8jr2+ItazBblK0ItvLq/R2UwBAehVWHEBAiNkOjtcL26zs1/EjL+gMvHweGdWjTX+U/K657zVzicrpmanD26LUgIbjEcGenVSC/bdlEM791LAhs4XBDumXjxohguKpIYadWqgh1zcmiTv4YqVrHnYhi88locPaokhgrHYNuQkUGr2OzTE8NesEkcParFmC5XVRtqAYLHQtILOcOFhZCa6roYrl4vinr1TmMM2dl60Erk6FHYuVOZ24YAZ97jkJsBw95VW9j5TyhfuMMNEsmHd+lLd99aWPS8rm99mfyLYdUUDbX4BTUSGPY+RHu4HsJgOFup0Vifo72rYO7fdbJZqxlMHg11WkOff8IfX8KmHzRbUyVMi1vrdYbej+m2ILFLBLcYBq96C3fu1HRqhWI4M5M2bATwzGLgxTGkpSlarUIhuW8fEeTTLPqw5zYJx/1UNjt2QHGxOredkpwcyMujVaMctm/3IHGvVi3ZDLxQkUxN1RgqFJIOQd+ymUSgxxYDL4whPV0nVy6J4YwMiI6mZcvTEMMABw548Mflk56u16Ei77nBz+xcos5xXe/TF+uMexWVNuRNrVxf97m+bGMS5WOs0ViLeRY+A3tWaBr3wFZY9Bwk3gjtr/X3iAyG4KTVpfLZL/+fcocv+0YV4VkPQZ/HoX5XNdwIrarPZ/pC2Zf6PA5128D0P8PRXH+PokKCXwx7ceGWq3FepcXwxo0ePFBMjPyRlVwFgxJx3rp1BTs6KtMtGuUHnN/WKaYqFMOOMbSKL6SoSM0h3MKyvFZV3bpV2worww5B3yzeokoVD8Wwv8cAevyYGFq0OI0xQKWLeud7wlSGA5jiQi2Eq94Qzn0WNk6EzT8p2D8yRl+udVpD339I7GZtggs/VsON3/4FnW6DZhfIQ1yzmbyPBoPBcwb+RyelP98MNZsqrWXdp7B1mha25mdroWv7MdDyEs3i5OyFoe/Cgc2w+Hl/j6BCzgwx7CWLgTtiOI5UqoYXey6GwSvVPKddwJXKMEDL5kWeVfICSQy30dvaI6tEdLR/haTjscMb1CUuzsOqqpcqw9u2aVthZTgnR63qoqNp3lxVcbfP87wkhnfs0NZUhgOYVe8pJ/j81wBLvsN650D3+/WlemCzrBP7N8KSlyDxZkd3rNvVQev811S1Orhd2adVa/p7RAZDcBNaVQtTCw7D9LvV3Ca2I0y7U3Fr/Z/VQteNEzVDYxfrc9tsECTeBL//B/Z5knfqO05LDFuWdaVlWd9alrWjsg7IbbxYGd64EWrWLAmtKJf9+6mCTasWpymGvSDqU1LU0KtRowp2dIrhNqFkZMDBg24+kDOWzEtiODzchTE4xXBiBBB4YjgkBJo0qWBH53sgJoaWLU+jqnrwYKV3Zty2TcXzuLgKdnQ+fzExxMXJlrBzp5sP5uXKcIVjMPiH/GxY8BQ0HQgJV8GiZzUlO+w9yEzWl2riTUqPmHqn8oXPf1kr3DOTVIna9Tus/Vjds5p40AjJYDCcTEw7pbps/F553Rd9qgzwWQ9Az7/ohHXWA5q96f+09tk0SUkTVWvBzHu9ljZVGZxuZXgfcDdQQWiXF/Gi39a5+r/CJJ7MTLAs2iScRiwZeGUcKSkaQ0WRZE4R1rKDhKTbIqxaNS1o9JIYjo93YQyOx67XuhbVqweeGG7aVHnPp6SUGG7evKSi7BZOIVnJ0WTbtumEpGrVCnZ0Pn/R0ccqsKmpbj6YFyvD9ep51nHc4AN++xfkZsKgV9RZbvnr0PFmJUrMvA/Ca+rLdZVD9F7wXziyVwvl2o2GuAESyXVaQ98n/T0ag+HMoudf9FmccY9mYZyL5HbMU3vmQ2lq1NH9Ifn5Z9ynNIr+z8KOuRLHAcppiWHbtufZtu3fNlGxsZqSPXKk0u96yxYXpuZBX/516tC6jUVKihYZuYUXK8ObNrlgkQAJyZAQWnRUNwWPfcNeEsMuvQ6O58+KjSE+vmRa3y28FOnlTj4vcExI7tmjxDq3iI7WtpJF/bZt7o/BWYENFDG8fbuxSAQsB3fA0teUCtGgq1avVwmFc5+HlCmwY448xAC//gOaDYb2ozVVG1ZdwnjBkxLRF34IYeaMx2CoVKqEKl2i4KBsEL0fU473jHu0kO6cOxSBmLnekQKTCr+/BJ3vVPbw3EegqMDfoygTr3uGLcu607KsZZZlLdvnjQqus6payUKyuFgCxiURtn8/1K1LmzaamXZbhHlJDBcXS9RWuHjO+dgxMbRspTK4x13DvCDo3RLDISFQqxbNmpX4Q93CS5Vhl4VkKYuBU7Slpbn5YF4Sklu3uh6rBhyzSYAHr4Wzy40XKsNGDAcov/5D03ADnoe0RZA8Hno+AlExyi+NbqfuVwuekndx8P8g6WtlDw96SVWpZf/VPnED/D0ag+HMJKa9ItU2jFNyxOA3YH8yLH1Fmd8RdeQrbtwXEq6Wr//IHs32ZKXAirf8PYIy8boYtm37fdu2u9u23T3WKVwrEy9ZDHbtUkXO5cqwI0YKPJjadlbyKllI7typMbjU6GHfPoiNpWZNaVqPI70qWUhmZSldy2UxHBMDVarQrJkHaRKgMeTm6lJJ5OaqL4zLkWSWBXXqHBNtbgtJL1SGCwslyl1KYShlk6hZU4l1bleGQ0IkiCtZDKenu+DbNviefWs13dr9QXW2mvMXpUn0fARWvqPEiEEvQ+YGWSS6/FlJEXMfhQbd5SOeeZ/8igP/7e/RGAxnNr0egTqtFHnY7HxoM1JZ3wUH1YEufaG8xef9C+wi+PWf0PJCNcJZ+KysUAFG8KdJOKuqlSyGnWLQHTHsrPy5XRmuWhVq1Kh0Mezy6n84JoYBzxdueUEMu5wkASViGFX/9u/3oCGeF4Sk83Vw2WJQpw6EhASUxWD3bs00uLTwzPm4deoA+hu3xwCVnopx6JAujRtX2l0aKouFz6mrXM9HZInY+Rv0fw6KC5QdHD8UWlyoznLhNbVA5/d/q9vVBf+D9d9A+iI470Ut1jEYDN4jNAIueF0V4WWvyaJkWTDnEeh0K8R00IlqjcbQ7QFY9xnsWaUT2vxsWPKyv0dwEsEvhr1UGXZLhDnEcOPGKmh5tOjJC35bZ0XRpWpeKSHZokXgtNB1PpcuC3rHGJxjdruq6hSSlSiGnULQ5dfBIcidFcxAqAynp2vrkpDMyoKoKEWAIDHskWWlkvOSnWOoMJXE4Fv2/QHJExTsH1EHFj4tH2LHm2DJq2rLPOglZZpumyEhXHBY06/tRkO9TjD3b6oQd7zZz4MxGM4SWl4IrUco6xt0Ips8QW3RB76kCMSV76r5RmRdCeXYRPn8l7+hha8BRKWIYdu2Kwof8x5eFMNVqrjoL3R4hkND9cXv0cItL/htnTYBl8ZQqjLctKmmxIuL3XzA6GgJIbf/sHycflmXKpKlhKRzzG5bJbwgJJ1jcGl6fv/+Y8cQGankA7eFZI0ald5Jz60xZGUdqwqDXguPKsOVfHLllqA3+I5Fz0F4NejxEKRMVsZw3ydUQVr+X/kOYzvC/H9CrXhZJOY/ob8d+G8lUBzeCYNfV5c6g8HgGy54DYqLYP6T0POvUK2+Fsm1GK4Frguf0X69H4ftM+Xv7/skFObqZDaACP7/HDVrQlhYpQvJLVskwMIrCo07elSZrg4B43GKgRfE8I4dOqxq1SrYsahIAqaUxeDoUSUZuEV0tIRwJbbQTU1VTrJTo56SrKxjOzqrsB6LYS8ISZcqkllZJdVp9Fq4LYa90EnP7cpwKTEcF6e3tts27EoWw86sYyOGA4iMJNjwrdouR9RVLFPtltBhjKZSC45Av6cUybR7ub5Is1LkL+56r1a3L31VFeLGffw9GoPh7KJWvD6H6z5Tikv/ZyR4UyZrNidvvz6fXf4kobzgaYhuCx2u10K6w7v9PIASgl8MW5ZXsoZdTjBwflkHoBjevt3FqfmsLIVhlxLDcBoWg0oUMKmpElMVZj3b9rEKPUDDhjpHCgSLQVoa1K/vwokVlCkkA8Fvm5am43da9E9JGWMAD73PpjJ8ZvP7S4pA6/GwvkD3rlJVOHe/plLbXQvRCYpMq9MaEm9QFSq8OvR6VPnCxUdLItcMBoNv6fO4fPpz/65W6HUT5BeO7aiFdcv+B0X5+rxunwWp8/UZLypQE50AIfjFMHjFb+tsuFEhzi9rhwiLjy9JcXALLwh6lzNVTxhDIKUYOMVwheTm6kl3jKFKFU3pu10Z9oJnOC3NjQSD/ftPshjs2OFB4x4vCMnGjV04KYEybRLgoRiuRNtNerqSLSqcKTH4hsO7Yf1Y6HiL4tOWvKxKU4cxikgrzIV+T8KGCUqb6PcU7F2jtq/dH4KCQ7DqfX0B13ElTN1gMFQ6kXWhz2Ow5WdVhQc8r4V1G77V57fgoARx57tUHV74tD6v7a+DNR9AXuXNJJ8ORgyXQU6OLAJuZao6hKAzMcBtIRkTowfOyXHzD8vGtnUMbkVhBbMYPiHBAPAsXi0yUhd/iOHiYsjOPskmcfiwB86TSk72SEtzo6JaTmXYo5kG29ZzUgk4Bb0hQFj5jqpD3e6HnUv0Rdr9QSjM021tRkLdtvDb/6na1O5aZQxH1IGeD8uPWCVEVSaDweA/ut6njnTzn4Q2VyhNYtHzjurwFTq5LSpwVIdnQ/pv6mZXcBhWv+/vowfOFDFcyRYDp7fQJRF2ghh2Cmi3EyWcCwErScBkZUlEuVUZdoyhVi2twfJ3EkNhofKeXXodnK2HSwnJQGm84bIYzs6W+KssIVnJlWGXq9sniGGnAHV+rlymkm03RgwHEIV5sOodaHkJ1G2jeKbwmtDxVljzMeQfgB5/gW0zYe9qLc7JXA+bf5RgzsmAP76ALncrvslgMPiPsEgJ3bT5Oqnt8w/ITILk7+Xzz8+W7emcO2SpWPYa1DtHi+yW/S8gutKdGWK4kivDbnkLT6iqOsWwv7vQOSuiLlWGT7BJWJaHC7cqefHZrl0eZNueUFVNT9diQLeoRL/tkSPShi4nSUDlWAwqUdDbthtC8uhRnYWVGkNEhH7dtcvNB/aCGDaxagFC0ljI2acEiYM7YMN4tWwNi1QVqXE/aNxb1olqDbTgZslLEBYFXe/R9VVCJZINBoP/6XSbbBCLnlcCTN02Soqp1wlaXAQr3tRntvNdimDL3qbq8OGdygn3M2eOGD5wwAPVUzZu5ZGeUFVt1AhCQ09DDFeSqHcrY7gcIelRC13LqjQR5hSAnorhuDiJ6d3uLlitRCHpdiQZHDcGpwB1viddpm5dKXG3zesns38/5OW5OAann6OUGAZ9LvxZGS4q0vvAVIYDhJVvawq16SBY/qau63YfbJyoVek9/6KK8LbpslHk7JWA7nQHFB2FtZ+o61z1hv4dh8FgEGGR0OOvygLfvUxxavvWwNbpOunN2av26V3vUwTi8jfUkS4mEZa+5sHCmMrlzBHDUGlVVbcrw2FhUL06gOdZw16qDLtsk7As+SMceGQxqFJFIsifYriM6XmPhKQ/xHAZY6hfXy/N/7P3nWFyVGfW5/YkTc55NMo5ZxBJRBNNMmDAkcU29re21+vsXUecjc3au04YG+wFs4DBBCOiQQQhhDLK0ozS5JxzqO/H6atujWam696u6jC653nm6Zqe7qq6011Vp84973mViaSDKr1yrBoQcWS4vp6E2JDhCED9LsakLfkEkyD2PAjMuhZIK6V6lDEdmPl+RjLFJTOWaet/8WK56gvANu+06uovh3skBgYG/lh2F5CYDWz6IZtrJBfQBjHlYt78br2Xtqa5NwO7/sAi2BX/yhSZmi1h3fWJQYYdJpJVVeS2aWk2XuztPudfZj95so8E2YYLZDgx0XefMC6am6nqxsScfKq0lLuiXM/noMVAiQw7qaqGWxn2I5JxcSTE4SSSwY4BYNRdOMdwpsSqCSFuFkK8K4TYJoT4+Sh/3zDiZ3XId/K9PwIxCcD824HDz9AuseQTQNNBoOINYMkn6THc/yiw8COAJw7YdT8voInZLK6b8wEga1bId93AwGAcxKfQx1/2LNBRyeWjLzBdYuW/MRXm+Ktc7u8A9j3MjPC4JJLjMGJikGGHvarV1QoXTb9sW4mSEg0ynJHhW58DOHGChNZWFNYoY4gEr2pFBQv5/ATrsdHcTObol5slbS5aZLi52ZFIL/k9UFJVR3wWQamqDnwWTinDtbWK/1K5DkOGbUEIMQXA3QAuBbASQIkQ4sYRL0uwLGud38+7Id3JwV42zJh9PSOZ3rsfSJ0MTL2UF0NPLFsq7/kLs0mXfop+wv52YPlnePHsa+PF1MDAIPKw9C6mvGz/NY/fmARg268YpZaUC2z/b7ZOz1vKm9yENBLi/Y8Afe1h2+2JQYYdTjFQqjqXyrAfSkq4DqULf2wsCbGDZNiWogpwDGOQYa0Obg6SYdtjkITej/3n5LBRhBYZHh5mZ8EgUVnJ1SUm2njxKDYJgERSawz+6wwClZX8txbasWeO4t0GOIaBAcWvRlwc74ZCTeijF5cDeMKyrDbLsiwAvwdwnfyjECIWQLoQ4jEhxBtCiLuFEDFjrcwVHHoK6G1hsU3bcfoJF98BDA/SLjHzWiApD9j5e6BwDSvOd/6OvsLic4Dtv+FzptucgUFkIrUImHMTZ4DikkiC9/yZN8ILPwaU/QPoqgOW3AnUbQdqt3M2aKCLhDhMmBhk2OF8W6Wq8zHIcH+/huPBwTgspSis5uZRxwBoKNwO+m2VyfAIEimEJpF08OZKqeFGSwujFyZNOuXpcPttq6po1YiLs/HicZRhQGMcmZmOtPeuqqILKC8v6FVFMrIB+JeL1gDwH3EKgNcBfBLAOgCFAO4cbUVCiE8KIbYKIbY2ONkMaN9D9AZPuYgXSIBk+PBTQE8TEyUq3wSaD1BVqtlCf/Gyu4CqTSzIWfYZm1NeBgYGYcGKz3EGZ89fmP4y0E2iu/gOwBpiLOL824HYSZwdKlzFm9xd94dtlw0ZHoHhYUWbxCiqariJpHLl/Cg2iaAtBg6gslKBDLe0nDYGgP8DbVXVITLsxBgaGniDZRuSjEpyGgSUM4b9t++FVJWVyXBGhiNkuLoaKCg4xRY/EVGHU8lvgfc5AIBlWa2WZX3a+zgM4EkAo3qGLcu6z7KslZZlrcy1VXhgA70tVILn3gxAsLK89AKS470PMbR/6iXMGY5PA+bdwg5zccnAgg8zgSI+jUqTgYFB5KJoDVCwgtan/OUsntv9AFurF59D1TghnQry3ofZbXLBh5lC0VIWll2eGGQ4KYlqmgMkrLGR07lKRHKEqirJj5bf1sHKedvq9ihkOCGBNgMtItnRocjcTkd/P7sAKtskRiASyLBuK2YJ+TkqRcSlpDDdwwEyXF1t0yIBcHtJSfSn+EGOQTlrODPTkTHU1ZEMT3CsB3C9ECLV+/sdAJ6WfxRCFAghviHESVn1cgDbQ7Z3h59mesTcm4HGPVR/594C9DQDR19kh7nBPuDQkyyQEx62dJ3zAQAWs0kXfIhFOgYGBpELIdhmvX4n02MW3cFZnoY9tEg1HwSq3uZr+tuB8ue8N8lg4WwYMDHIMOCYqqrkLezuZgCrkxaDUBcLDQ1ReRuFSIZzer6mhklKSjcloxBJSYaVIgwdUlX7+nhzpUQkx/gcAMXPwuOhquoAkaytVRzDKJ9DuJXh2tqJT4Yty6oB8EMAbwghNgOosyzrCW9qhFSJUwBsF0K8CUAACF0v1AOPA+lTWTyz/1GS3Tk3kvwOD5AMH1nPKvP5t/IC2d/O6dSDT7CgbuFHQra7BgYGQWDerUBMPLD7QWDB7UyF2f0AMPcmzvbs/V9g8vmMX9v/KJA2GSg5N2y+4YlDhh0q3JIXa53ucxJ5eayHiwoyLFsAO62qOkCGAQUSNo4y3N3NYdqGQ2S4zjtBHSyR1LasOKCqDg7SomGbSI4xhoQEfjW0PMMOKcP5+UGvJuJhWdbDlmUtsyxrjWVZX/I+t86yrFqL+Ib37+dZlvVZy7Kc6VQUCL0tbKAx5yb+fuBRoPQiVpfv/z8gcxanU/f9lV2sSi9kckRyAf3Fex/iawpDnwRnYGCggcQsFsTue5iWiJnX8DiOTWQb9kNPArA483PkOaCvgwS6cS8V5BDDkOERCKb7nITHQxKmRYZbWqjWBgGtMUSYxUCJDA8OMvlhjDEAiuNwiAxrEfox1G0gPESyoYH3SsGSYUBzpsEBZXh4+IyxSUQuyp9jYsScD7AIrqWMnuCuOuDEa1SFT06X3uJbnvdBtms9sYEWCVM4Z2AQPVj0MaCnEShfz2O5u54FsnNvZr74idd5HhjsBcqf9dmjwmCVmFhk2CFVVQibF05J+EaQYUCz8UZ2NpmHkox5OqqrWShkSwkbQ90GSF7q6xW7XDuUxKBEJCVZcooMJyTQ9xokkZQe32BtEtnZTHIIBxmWY3CCDBcWanqGOzp4w6OJ5mbeXxoyHEYceZ6RaYUrSXIBKkXlzwHWMDD7BqD8eVoh5t7CZhxD/d780UcBWLRLGBgYRA+mXgpMyqLff/qVVIUP/g2YfgWtEgcfB4rXAinFrA9IzuPv5f8I+a5OHDLsoGfYdozUOGS4pESjgM4hv21VlULl/BjqNkAiaVmKhVsOKsMej0IHPWBcVVXLYuCQ1cMWCRsYADo7Rx2Dx6PZwc1BMhys1QMIQhkGgrpBlGM4E2wSEYnhIRbITXsfVZ/y9fQNJ+eTDKeWMFap/FnaJorWAGXPAClFjFw6/HcgfxmQOSPcIzEwMFBBTBxbrZc9y4Y606+k/z82gTfDB5/w3gxfDxx7mQrxjKtYeNehetEODhOHDEubhFKl1OlQargxjsVAdqFT2h2HVFWnxqBFJB30DOfnKxL6cYrPwuG3ranhLIMtEjZGJJmElmXFgYxeJ5XhoiL+T7S60AXxWSiPwcBZ1G5jhvD0y5kcUb2JytBQPy+A069k9uiR57k8PEDyPPP9nFat2kTvoYGBQfRhzo20PR3/J20QXbVA5UbOBvU0AtWbeT4Y6GY79hlX833l60O6mxOLDA8Ocko1CChnDMttj0BJCdMElHitQ8pwdbVirJr/tv2glWKQnExZ3QFlWEmNBEYdw6RJ/HjCQYZra6lsx8baePE4YwCCUFVbWoK6QVRSVcdRtwGOYWiIPmTbkMpwEKReFjIaZThMOPoCAAFMvYw5w9YwSW/Fm0yOmHEVCW9vCy+EJzawG9XMa9itChbVJQMDg+jDlEuYD37wCWDm1UyYKHuGFgoRw5vg0nVswFG+HshZwOzxI8+FdDcnFhkGHLEYKHWfS06mx3QEZD6ukm/YwTEoK8OSdPhBSxkWwpFiRqcIPaCpqspixiBQU6OgRo5j9QA0yXBmJglqd7fiG32oqQHS0222k5aEdRzPMKA4DqMMRz+OvkSvcFIOiXFiNu0PR9YDMQnAlIvpEfTEAdMu44UyLokpEmVPA2lTaKMwMDCIPsQm8Ia3/Fke1yXncuZnUgbbqh95ns+XXshzghB8/bFXOHsUIkwcMuyAxaC3l28PpvuchFbWsAPKcHc3OYkSGU5PH1W+zMmhyBuOLnRKyrANIhkuZVhZ3R5nDG1tQFeXwg44RCSVLBL+2x0BuZ66ulH/PDocUoYTEoC0NO1VGOhisBeo3QJMXsffK14HJl8AeGKYIlG8FohP5oWv+GwgIY3kecrF9Bcf/yfVJJMiYWAQvZh+OdMj6ncB0y4HGnbTEzztcqBuO1Nlpl8BtBxm0syUSzg7VLM1ZLs4cciwA4VbShnDwKjd5yQkGVYqopMXfgfGoKRuj0HotQu3gsxLHhxkioUyGR5F3Qb4v1AqAgQcK6BTJpLj2CQAxXFEGBmWNgUlMuzgGAyfCgNqt1LdKTkXaK8E2o4BJecBfW1A3U6G7ve2smCm9EKgvQJoLWcGcc279BFOuSTcozAwMAgGUy/l49GXWEgrl6df4V1+0Xecn3gdmHwelyvfCNkuGjLsB6VmFXJbY5DhvDySSaUoqdhYErogSJjyGMYh9HI9WhaDIMZQX0+bqxIZHkPdBkiE6uoU45szMymza7aVHh5WVIYDqNuSSE4EMqw0BoeUYeMXDhMq3+Jj8VrmiwK80FVuBGBRJa58iz7iyRfQLwzQQ3j8VQACKL0g9PttYGDgHFIKgdxFbLyTu4i/H30ByF/K6LWKN4DsuUBiDs8TSblA9jwS4xBh4pHhIEiYsjI8jqoaG8sLcKhVVS0yPMYY5HpCTYaVm1WMkc8rUVhIIqx0nxQkkWxupsKtbJMYQ92WhDSayXBKCi32SspwUhK9OqEag4GzqHyLF7Uk70UuPpX+34rX6REuWsPlmHig6CxaJyZlAXmLSYYLlgOTRv8+GRgYRBGmvY/ng4FuzvxUvAFAeG+U3+LUXcm5fjfNFwBVG9msJwSYOGRYXoAdUIaVCrfGUVXDYTFwgwxrjSGIz8Gpzm0Scj1KKr38n2iSMKWMYbmd1NQxA67DQYa7uhjO4hQZBrgupTEIEXQXOqMMhwmWBVS9DRSfw98rNwJFZzNvtOJNZg3HJZEMF64B4hKpDJdeAAz2MYKt9KKwDsHAwMAhlF5Iy1TNu0DJOYxYaztGAtx8kJ7ikvOA1iNARzUtVP0d9BmHABOHDMfFsUImSDKcmDimOHcqLCsgGZa5qkoIkkhWV1N9S021+YYAZLioiIRIKbEuOxvo4jWR7QAAIABJREFU6eGPBrTI8DhjkGRO6bOQhE7zxsRpQp+TQ9tNKMmwVHCdKgIESEqVlGG5Ps0xyCg3owyHAe3HGZdWuBIY6AEa9wKFq6n01O+gEjzYR+9w8dlAVz3QdhQoWsuimqF+XjQNDAyiH0Vn8bF6E9VggMpvyblcrtzo5xV+0/f62tAU0U0cMgwEHeklI8lsFdq0tfFKG4AMK6uqQSYxKI1heDigxUArXs0hVdW2mheADEsyF0oi6VQrZomYGPrQlcYg4xM0VVWthhuJiaNGDUooK8NAUMpwYyO/5kYZDgPqdvIxdwmJsDXETnJNB5gykb8MaNzDJhv5K9icA2DsWs0W7/Lq8Oy7gYGBs0jMArLmMlM8ZyEtU1Vvc4YoJoHEOG8pLVO124D0qUBCBlC7PSS7N/HIsANE0hYk6Q6gqtbXM+rVNhywSdgeQ3s7mYJbZDgIVTUnB4iPt/mGAEQyKGU4lDaJcRRVuS4lIhkTw8LCIAm9k2PQUoZl8xANmIzhMKJ+FwDBgpm6HXwuf6nf8nIfAS5YwQg2CO/zW9imOcXu3aSBgUHEo3gtlWHhofJb9TZziPMWczYoJo5EuX4nFb2C5Xw+BJhYZNgBi4Fys4oAnmFAkcDIZg9K0Qc+aHXQC0DoAU2/rSYZrq5WUFSlXWUcEpaURJFU+XMAgiLDKSn8sYUAYwA0VdUgLAZuEfqmJsUbxCDaSkvibchwGNCwC8iaxRzh+h3sQpU+jRe32EQgew7JcEIGkDGd06HZc4GEVPoKjSpsYDCxUHw2W7O3lFERbtxLO1TuEt48WxbV4bodXM5fzkziIZULhh4mFhkOwiZhWRrd5+Q2x4AWkczO5s60tSm8ibAszc5tNgi9kt3DAWXY9hg6OxnbMA6hBzgOpc9BGseDUCSVCFgAdRsIPRmuraVPOSfH5htsKsMAZ0xswwFl2NgkwoD6XbywAbRM5C2h2lO3A8hdzEK6+h20SwjB6dCCFcwglhdLAwODiYP8ZXxseI/ngOFB2qbyl5Ikd1TxNT2N3uXlwFAf0LTf9V0zZNiL5magr88dVTVURLKxkbG4yur2OGNITeWP1hg0Pwut7nNOE8m4OMq6QRB622MAbKuqdXV0tthGkGQ4L49uC1uwOQa5btuQyrBlKbyJMMpwmDDYB7QeZawawGrxnAXe5QNctixe5HIWAH3tQGcVp0gbvRe+3IXh2XcDAwN3kD2fFomG3bRGACTGst16wy4fYa7fSYsVADTuc33XJh4Zbm3VshhoRZLJbY6BUJNh5e5zNomkciFgEJnPys0qbCQYABrKsFxnEETS9hh6etgL3AaRHBhQ3KUgx6BEIm1YPbQbbwwMsAmKImpraZOxbVcxcAZtxwBYQMYMoKcZ6G0GMmeS9HbV0T7RVQv0dwJZc0iWAdokpAokibSBgcHEQFwizwMNu4Gs2SyWq/eqxABnk3Lmc7n5IM8fANs0u4yJRYaD8HlqdZ8Dxr345+ZymjlUqqoke2Enw8nJVFY1yHBTk2KzCgVlOJRk2MlWzBLaqmoorR42lWGtlswavmHTcCNMaC3nY8YM33LmTNofACBzto8AZ83mVClAYty0n9Xl6dNCu88GBgbuI2chybAnlkpxw24gIQ1IKQKaD7PJTmI2zxVxiUBaKdByyPXdmlhkOIiWzFrd5zIyxp1DjonRIGFBqKpa2bZAQAKjTIaF0E7F0B6DDc9wVxctxrYhixkVIZtVOK1ua5HhIP22tscwMMB/rlvKMKBFhk3DjTDhJAGe4UeAZwHN3ota1iw/MuxVhj2xJM9N+0mQPXb9OQYGBlGDnIU8Jwz28Zww2o1zxkyfGpw5iyTZZRgy7IVUhm1f/JuaxrVISCgTSQdsEkpEcpyuZxJyDEqWzQgkw/7rtwVNVVU5zsvmTYm2MtzXp9wAZXiYRNL2GCRRDTCGxEQme2gpw5qfhVGGw4CWciAuGUjK85JhwcSIVi8xzpjBC1xMApA2mRe+9GmMVmo5TOXYwMBg4iFjOgALaD/B5bZjwPDQOLNIs4wyrIwgVNWqKtoabGfbBug+J6FMhqUKpkkkMzKASZNsvkGB0Pf1KXIRzZg7ZTLspqqamRkaQu+2TQJQVlVbWij2OtmKWUK5mNEow9GHjhNA2hTOEnVUAMl5QOwkoKMSSMplG+bOKmYJCw+fTyvlHXdHBZcNDAwmHjK89qe2oyTDwwM8F2TOADqr2a0ycybJ8mAfSXJvC+sNXMTEIsNB+G2VmlXIbdggkoWFimQ4NpaNEjSJpFKCQYDObRLaEXGhUoYTEig5joNQKsNu2VXS0nijE4pOeloNN/y3Nw6UG29ojmFggAkrRhkOA7rqgBTvP76rFkj2Hgyd1acup3hPLh2VQGoxL3oD3VSLDQwMJh7Sp/Kx7ZhXJQbQesRXLNd6hDfSsICuGl/jnU7Voh81TCwyHKRNQpkM2ySSMvLMNoIgkraL5wDbZFg7a1jT6pGeHpDb+iDHEKD/tJaqmpXFlIfeXoU3uUckhdBQVSOQDIdKGW5o4KNRhsOArjpaJAAvGfZ+kTr9L27VJMDWsHe5hKQY4LKBgcHEQ0ox4ImjMuxPjFO9BKyrxu98UXvq+cJFTCwynJ7OqjXNAjplImnTYgBokDBNMuymMhwKMuzWGLKyaI0ORUvmmhoK/ErNKoTg9zcAQkWGtbrP+W9vHCgrw5oNUEwr5jCiuw5I8t6FdI4gw8mFtENIZbirnuH7KcW0SABAqlGGDQwmJDwxPO47Kn3nhe56381zd/3os0pdRhm2D80Ug/5+dsSyrQwPDrJDnAIZViaSioRedp9zg0hqK8NdXTQbK8CNZhUAI+7y8zXJsOL3qaaG2/LYPbqam0n4bLxhoijDra0KgntsLIOCFZVhSbiNMhxiDHQzPzg5nyemrlpe3KxhkuSUQqC/g69LLuTfAV4Yu7ytCZPNh2ZgMGGRlMuOc3HJrCXobvAd8111PpLcVWtsEtrQIJKSIDnZuU1Ci0hqdNJraSGpt00kLcs2GU5KIlcLRSqGW1YPgP+bUBFJp1sxS2hbDDTGkJjIsBFbUFSGAQ3fsFGGowM9jXxMzCEpHh4AJmUD/V1UgCdlseUywEzRk8sZQF+r73kDA4OJicQcEmAhqAh31wMJGbRPdNWRLEOQDCekM3WmS+WCoY6JR4Y1iKQb3ecktIrPNPJtlYu22tvZqc8mCQtFFzrLcs8mAWh0oQvCYuCGug2Q2DU2sjjMFoIgwwUFAa3YPrS0sLrPRpSJVuONjAyjDEcL+r1h3vGpwIBcTqEaDAAJqT4CnJDmI8AJ6Sygg+DzBgYGExNJOb6b5qTcU4lxVx0zxydlUD0W3vOBPH+4hIlHhjVsEtrd52yQ4dxc2piVVdWWFoa92oR29zkbY5DrdVsZbmvj1LlbZFhZVdXsaOhGG2MJud76epvrjoujxUBjDEqfQ2ur7TFoNd7QVIZTUzmzEWkQQiQLISZmV4kBb9vs+GQ/YuxHhuNTfTFJ8Wl+xNirDCekM27NwMBgYiLRS4ABzhpJYpyQ5ruBjksBBrq4HJ9qyLAyNJRhSfJsE0m5fhskzOPRiFfLyqJMqqCEudWsQiIUZFh5DP399CXbJGGFhUwYGBy0uX4NZXhwkERVWRlWIPSABpFUVFXdaMUsEUplOFIsEkIIjxDiNiHEc0KIegAHANQIIfYKIX4mhJgV7n10DPICFpfstzyCDPd7yXCCPxlOB3q9ZNjAwGDiIiGN5wZrmDfNA96mUKecM5JPnWUyZFgRmjaJhATbIqmSMgxokGENi4FW9znANoEpKiJZtS1Wh4IM22xWIVFQwHsM2yRMowFKfT234aZNAgiNqqpMhuX/KwDy8nzbsA3NMUSQReI1ADMAfA1AgWVZky3LygNwHoB3APxYCPGhcO6gY5DKcGySn8qTPIIMy+UU3+vjkoChPiDWbq6igYFBVCLWa6cb9B7vg5IMJ/nNLKX42ayigAwLIW4WQrwrhNgmhPi5EzsVFLKygO5upWzYqiqSPdv+SA2LgbJn2H87NlBTw9nwlBSbb9AYw8CAwn1GKMiwIqGX67VNwmJi2OlCgYQpF21ZVsSR4f5+fs5KZFjBJpGQwJeeScowgEssy7obwJ8tyzp5S2lZVjOAKsuybgTwaLAbCXQ+FkJ8TgixRQixUwjxpWC3NyoG/cjtScUnkYV0AOCJZ/tVgAUzw96pGk8sX+OJdWW3DAwMIgQxXjI81Mub5pPnDD9lOD4lepRhIcQUAHcDuBTASgAlQogbndgxbWioqloNN2JjbZfah8pioOy1BZSUYUBhHKmp/B8pqPTK6raiMqzVhU6xmFGZ0Hd20lsRQX5b6Ud2yyYBcBzKY5BFnzYRYcrw9UKIHwNIFULMG+EXvg8ALMuyWxY5KgKdj4UQ5wC4FcA5AFYDuE4IsTKYbY4KSXRPGaLgjZ/vRd6nPYDl9/rhQSAmzvFdMjAwiCDEeWd/Bnu5LG+aY/2U4ZhJJMsAzw2W/XO/DoJVhi8H8IRlWW2WZVkAfg/guuB3y4e//x24+26FN2h0odPuPmdTSi4q4ltsR+5qtJVWjiRTiMICNMiwRuZzTQ2LnWzHeSn6nkOhqrqZzwswrCEjw90xSEKvRCQVbBIA/z9ajTfa2my9vK+PuxRBZHgjgH0AMgH8AsBhIcR2IcQ/APQ4tI1A5+OrATxgWVa/ZVn9AP4E4FqHtu3DyeI3a8QfvL8LQa+gfO1J8uwBhowybGAwIdHbArz2ZaBmq08ZHuzxzhR5W/QKj+/cwCe8DyNvpp1HsGQ4G4D/ZbkGQJ7/C4QQnxRCbBVCbG2Q/VEVsGEDcM89Cm9QVFVlswo3us9JKMeraajbWspwUpKtKCwgNF3o5BiU4rwAZVVVOV5Nw+rhFhmW61bOGlYgw5Kk2v4+DQ9TtVVUht2MudNSt12EZVlVlmX9BcC1lmVdYVnWdACXAPg2gIsc2kyg83HA87VEUOdteQBbIwoMTl7MRpBha4iPJ0nyxCtlMTA449HbArx7D9C4F74bZe8xf3IWyRojSUbg9JtrZxHsWacOp55MC7zPnYRlWfdZlrXSsqyVubm5yhsoKuJ1trPT5hsUleG2NlqMlZVhDTJsm0gqFm652X1OQpIKZYtBBFk9EhK4S8okTFEZzsiwfY8RGjKcmckveX+/rZcrq9ttbfwSKo5BSxm26RuOtIxhIcgQLcvaKJ+zLKvZsqxtlmV1+b8mCAQ6Hwc8X/vtm/55e0xlWP7db5iW5Z0CHeZyjJ9KZGBgMHEw5HWBxYyoE5A3w4CXGI9yGowCZXg96IWTE9t3AHg6yHWeAklSZRZwQCiSYeWMYbluBSKpTIZjY4H0dNtEsqODXMdNMpyQAOTkuK8Ma1k9FKbntRpvKJJh5SQJuR2bKChwV1WVZDhvVM1wFGh8DgUFvMHt6rL5Bs0xRIoyDOA1IcRnhRCl/k8KIeKFEBcJIf4M4KNBbiPQ+fhpAB8RQsR5PcsfBfBMkNscBX7K8EmVeMjnBR7q9yVGSM+gXI6dxApzAwODiYWTBbRxPv+vJ/Z0ZRijaQIRrgxbllUD4IcA3hBCbAZQZ1nWE47smRfKRFLRJqFNht1UhgGlttLKRVuAMhmW63drDICmMpyeztQHm1Amw7KAzuZdaU2NRuEZ4L4y7L+tAKit5VsSEmyuX6q1imMANGLuolQZBv28QwAeEUJUCyH2CSGOADgMFrXda1nWg8FsYKzzsRBigxCiwLKsrSD53QzGuT3rfc5ZxHi/OIN9rA4HWBRzcrmLSRMAq8hPEuMevnfIfhKQgYFBlMCfDI+rDHuXhwd9y0N9vvOKSwi6UsGyrIcBPOzAvowKZWU4KYlXcTeVYUXPcHY2G4EpZw3bJPTK3ecArnvOHIU3aLZktjmGri4q3G41q5AoLAQOHVJ4Q2Ym7QU9PbZamdXWAmvWKKxfkwx3dVFZtRWlp0GGQ0Ho5bamT7fxBsUxRBoZtiyrF8BvAPxGCBEHIAdAj2VZanlxgbdz2vnYsqx1fsv3AFCpwlBHgleY7u8AUgr9lr0nqIEuYJL3uB3o9ssc7fEqw4YMGxhMOPjbJIa8VihPLG+aJdEd6PbdKA90MlIN8N5AJ7u6exFfqaCVYqDQeEM5zqunhz8KJEwIzXg1RTLsVqMHCa0xdHba8qpqq9uKYygsJAGzbT+S67fxWViWpk3C41GI0NCIiNMgksoZw4CyTQJQULjluhXGkJam4N0OEYQQrwCYb1lWjdNEOGIQn8bH/nZmhQLMCx1NGR7wU4aletxvt0DEwMAgaiBzguNS/Nqxp7IDpew62dfud/7oHP384RIingynpvLHtjIMKBHJqiq+PNFu0yPF7nMSWkTSLUIPaNkkiopIXmxHvcr12yAw2oReQxnu71ewMisQSend1urc5rF/KCoTyQhUhpXzkpOT6aW3aZNQHkPo8BUA9wohHhBCqHzbowfxfsrwKcv+F7YU3/OTvN+b3hYgMZskeiioyGUDA4NIQ6/3OjEpE+hr5bnBE8vjPUESYL9zxkhlON5uRzE9RDwZBmhhUJ6eV7BJKFsk5DYU4KbFoKaGClh6us119/SwQ58GGR4aAmwnLSn4t7UIvYa6rdyFToHQy3W6PQZlMqwwBrle5YxhQEkZzs3ljIltz7AQSsWMdXWRY5Hwh2VZ2y3LugjAPwC8IIT4thBiYvUflhe2vvZTSW+C9/vR2wIkeRMqehqARP/lHO+y/VoDAwODKIA/Ge5t9Z0P/JXhkcRYnj+MTYIoLlZUht0kw6FUhltamOEaAMr5vIrNKiS0ixltfBahLAL0315AKBB6rQSDIAi9GzYJ6UVWtknExChZPWJjSYjdah4SqWQYOBmhdhDAbwF8FmzA8eHw7pWDkNOcfa1AbAJ/767nckI60F1HBRgC6KrzEeNufzLcGJZdNzAwcAl9I5ThSaOQ4b52qsGW5VsGSKQT7Kp9eogKMlxU5K5NQosMaxDJtjaFKKmsLH4hbHTcUo4kCzUZtvFZ1NQA8fEKu2RZEUcklRtuyPUqjiE7m2TSNpGMi6PNwMYYpFKrZfVQjMl1s3lIhLViPgkhxFsAqgDcC6AYwMcArAOwWghxX/j2zEHExJHUdnoPiJQC33JyAdBZC3higKQckuSTZLiRzwEkxgYGBhMHPU1MkohL5rIsou1u4M3xYC+V4aQ8kt/hAZ4v+jupDCe763uLir6XxcUkGsPDNq2VUhm2rHEv0IODvPgrEckglGGA45g508Yb/FXVAGSpuhpYtEhhZ0JFhhU66clIMtt8qqsLGBhwnwxrKMPKNokpUxTewGNAq4Obm+q2gkVCQisizsYY+vooVkeoZ/guAHu97ZL98VkhxP5w7JArSCkCOr0niuRCoMv7QSfnUxkGeNHrrqf6E5PA52XiRKfKNJqBgUHEo6MSSC3mRb6jEiheCwz0AL3NQEqx381zkd/5ooCzRwDPHS4iapThgQGg0e7MWXY23xCgbZ1MFdDyDEcYkXS70QNAAiaEe8qwVsMNxc8hJYU/tolkairZp03PcFyc4r9VQxkGNImkgu9ZSVVtbQ3dGGwU0MlWzJGoDFuWtWcUIixxVUh3xk2kFPoIbUoh0OWnDPtf6DqqeVJJKwXajgNp3hvDtmMh32UDAwMX0V4BpE5mlnBnFZBa4jtHpBb7nS+K/IhxoY8MJxkyfJKsOk3CtBtuJCYqxE8QblkMurvZrlqrjbEikYyLY1cy22NIS6OX1A1Cr9iK2R9KHdw8HtuKZE0NCZjtYAhNqwfgi4izDelBD4BQ+Z4B/q+UY+7cIvQRAMuyjoR7HxzDKcqw1yZhWVSAOiq5nDEdaPMOOX0a0HaU3eiS8w0ZNjCYaOio4E1vdyNzhlNLSIoBrzIsifEIZVjOJKW4O9UXVWTY6ZbMoeg+J+EWGdYuPPPfhgKUCgFlAoCb6rbGGLS60Nm0GCiNoauLXh2NMWi1ZLZJJD0eFrfZRhA2if5+W7Z4Qo4hAHvW8j0bOAs51Tk8CKRPpeevpxHInMk84a5akuHuBqCvA8iYBrR6iXHaVEOGDQwmEoaHeBOcNpmPAMlwh5eEpRb7lpNHzCr5P+8iooIMSyIZEWRYsfucRHo6xWSnkxi0u8/FxtpsX3Yqioo0iGSAMfT1cZdCpQwrk2EFIul2Pq9EQQEj7mxnPtscQ10dibBCh+ugbBKAYuONoaGA9qdI6z53RiJjBqdD246RAANA82E+DwAtZUC6t/Vg2xES495mVpCnT/UpxgYGBtGPzireGKdNAVrL+Vy637J8Pj6NxXQtZSzCTUjj83FJxjMM+AqrnFZVq6s59Z+To7AzTU1aSp5yFzqbnc+CarihWP0PuJOXrN1wA4goZVgWAdpGEGS4sJAFpbYzn90i9EFYPdxqHhKtNokJhazZfGw+BGTO4nLLYR8xbikjAQaoCEti3FIGZM8DWo9SQTYwMIh+NO7jY858oOkAl7PmAM0H6SOOT+b5IWsWeYn/uaK1nDfRGnxFBVFBhqVX1Q1luLBQqfmXtk0CUCSSsbGUk92ySWiQSIBjqKvj7L4t2CCSQZFhTSLZ2RlQYPTBBpEcHCQxDdUYJJFUiojr7qYMPw6UI8m6u1msqmmTkNu0Bfl/ClBEF6mtmM8o+JPh9GmAiOEFLq2Uy61lvPABvDjmLuRyw27vsgU0TZxwDQODMxryWM6eDzQfoBIcl0QynDWHf2s+BGR6zxsth/1uost8xNhFRAUZBhS70Nm0GChnDAPaNglAs/GGDSIZF6e4S83NWgQMINmzLIXOYW6R4SCsHlrxagHG0NDA/0solWHAHVVVueGG//oV4JYyXFdn/MJhR2IOO0y1HGLucPpUXuBi4nhha9rPEP20UqDhPT4Xk+Alw96cyIbdYR2CgYGBQ2jcx3NCUg6P/ey5vGA2HQSy5wCDfbRUZc3mjFBHJcmwNcyZI2mvchFRRYZtK8Px8SRJNtIklMiwZTlChm1Xz9vw2yp3nwNIJoJQhgHFGxO3lOHMTK2pEy0y3No6bjdA7YYbQGiUYRstmeVNTqjGkJnJGznbN1ZSfbZBho1FIswQghe25oP8PXse0LCHy3lLgLqdvuX6XYAnFshZQGKcMcNLjPeEZ98NDAycRdN+WiSsYa8aPJdFtP3tVIZbygBYPGe0lPE9mbMYxzbUZ5Rhfyh3obPRklmZDLe3a1f/AxxDVxfQ0WHzDTb9tkokEgjaJgEokuH2dk6lj4GaGo0EgyDVbbldW8jMDNgNULvhhly/ItxQVdva6KLQIsMaNgkhfPFqtqCgbhsyHAHIWQjUv8djJ38Zp0cHuoG8pYxR620Fcpfw4jjYS0W4YTe70+UuBOp3hHsEBgYGwWJ4kMdy3hIqwQPd3hti7/GdtwSo994c5y72W17Em2P5vMuIGjJcXMymGwEsjz4EIMPt7fSMhqL7nIQbqmp1dRSQYWBcAiMLz5QSDIJQt93oQqeVz9vczLuA1FSFNxGJibSUO0kktRtu+K9fEUqNNxRsEoYMRwAKljNOraMSyF9OVaj+PZJhgBe6vCV8vnEvn++qZZRS4Rqg5l1GMhkYGEQvmvaTABeuAWq38LnCVUDtVgACyFsG1G4DYhNpn6jb4V2e451BEj7rlIuIKjIMOOfzlCpzSYnCTsj1hZIM27RJ2MbAAO8ENIlkXh75m5Od9LTVbU0ClpVFJ42TFgNtm0RGhmIFpw9KWcMKZDhUNgm5LdtkOC2NcvI4BXQR3or5zEL+Cj7WbqMyDFAhyveS4bodJMwAULOF7VkBoGoTUHw20N9JkmxgYBC9qH6Xj4WrSYDjkmmbqt1Gi0RCKlC3nTfGnlieF3IXc7l+Jwtt49Vrg1QRNWRYq53xOESy0pv7rESG5fpCpapmZ5NsjOFV7e0lJ1RStyWR0BxDTAyJhpMxd1pkOAhlWAhNRTKAMpyRoZhgoBlJJqHUhc7mGIDQ2STktmyPwePhdsYh9CZjOIKQtxgQHl7o0kqBSZlA7XZ2lUoppPKbPo35oVUbSZJjJwFVbwNFZ3Md1ZvCOwYDA4PgUPMui2kzZ/KmN385rVC1W4HClZwZqtvunT2ySIBP3jzv9M0kuYyoIcNaXejGIcNaynCQNglJ+JSI5DheVbke5aYhct2aUErFsEGGta0eQRJJp20SympkkGTYaWVYq3ObvLkKggwrNQ8xZDh6EJfEKKXabd470FVAzWYuF58LVLzpW658C4iJ52uq3mYGcVIulw0MDKIX1ZuoCg/1U/UtXAV0VLPLXP4KNuPp7yAZbj0C9LWRDPe28ve8JSHZzaghw8pd6LKyxlVVpTKs5RnWJJKpqfxxikhqddALclob0CTDY9yYaOXzDg/zBiEIQq9Ehm0QSW11O1TKcGwsv3wBbBJxcYq71NLC9cbGKrzJh/x8EuEAbiAfAmQ+GzIcYShcBVS/Q/Vn8nkskOtp5nJHBdB+Aig5h7FKHdW0StRtZ0FdyXnA8dcU4ncMDAwiCl31POZL1/E8MNQHTD4fqHidf598HlD5JpdLzuFNMcDzQJV3VkjOErmMqCHDWVlAQoKixcCyxvQXVlay85zStHaQZBhwlkgG5XuOEGW4ro4fkxKRbGvjm0KlDNu0GIRDGe7qcq55iExhUI7p01SFAc1UDKd9zwbuYfIFbLPcuJcXQYAXvJLzuFzxJlB8ju/5yRcAwwNcnnYZCXPzofDsu4GBQXA48Rofp1zMZeHhMX5iA1sv5y0lMU7Op3+44g3aqXLmA1Vv0TdcuDokuxo1ZFgIxazhAF3otBpuNDXxwq+pggGKRDJA8ZlUt8Nhk2hsBPr7bbw4PZ1ezzHGoN1wAwhqDAUF/DhtjWHSJCApKSAJCzUZ1oqIc3oMra1BE3q5bVvIzBy3gM4owxGG0gv4eOJ1XtRi4qkE5S7ixbDyTU6JxqcCx/9JwhwTDxx9EZh6Kd8yl+iiAAAgAElEQVR77OXw7b+BgYE+jr/K47xgOZfzlwGTMoCKDTzWhYfnhpLzSfIq3+CNsvDwRjl/OVs1hwBRQ4YBZxXJykpFRRUIqhWzhFJesg2bRHIyi+xtwyEyDNgkMB4PCYyTZNgBq4dWB7cxxtDRQYVWaQyW5YgyDDgzBkCzc1s4xhDAJmFaMUcQ0qeyeK7idRbHFa7hsieGU6THXmFXuikXkwDHJfFiePRF+oYzZgDHXgr3KAwMDHRw/J+0SAz10yZRehHtUM2HgNILmTfeUcGb5s4aNtyYfD470tW865tBCgGiigw7rQyHiwzb7kJngwwXFytOa8t1BTG17WResiTDSt5tua5Qqqo2xqBEJLu6aJh2gEgqjSGA71lZUQ21TSJAAZ2Wum3gLiZfwOlPy+KFsXYbfcPTrwBay1lAM/1yoP04G3BMex/QuId5w9Mu4/TqYG+4R2FgYKCCpoM8vqdeSlvE8ABveo+/wr+XrmNNAOC1Tnh9xCXnMWliqA8oOTdkuxtVZFiqqraI5DhkuLeXRVtaNgkHyHB/f8BeGoQkSk5aPZqbSSiUOlycCqfJsOxEZhuSDAVZQCe3bwvjKJLhKmTUUrfHGMPgIFBfr3hTAgRtk0hJoQPFdkvmzEyGCff0jPpn03AjAlF6IdBdzyYb069kMd3Rl0iGAeDIehJgADjyAgmwXJ75fuYNH3slPPtuYGCgh7Kn+TjrWqDsGWYFl64Dyp5ltGL+UuDIc0BqCVuxH30BmJQFFKzgzJDw+OoMQoCoIsPFxUB3N3tGBMQ4qqokceFShv33YVzExtJzG0AZVkKQ09qAs81DqqtZyBgXp7ADEaYMa0XcOUCGs7L4FXGCDNfXM6RDmQwHqQwDmpnPY/iGtVI9DNzF9Mv5WP4c0yUSc3gRzJjOopkjz9NOkTWXxDh3MX8/9CQw5SIgIZ3LBgYG0YNDT9Hzm1pMMjztcipfR18EZlwNDA2wHmDG1QAsngemX04L1ZHngaKzgER9wUsVUUeGAZtWiYwM/uNHIWFaSh7AqrGcHMU3nQqnVNXhYa5DmdAH0YpZIjubJEypEHAcQq88BgeIZF4evx5OWAzk90mJSDowBo9HI2u4t5c/IyA/S6UxDAzQ7hHkzZWTLZmrqzUIvYG7SCkEClYCZf/ghW765VR9h4eoDp/YAPR3AbPeT0tEbwsw+0ZeKAd7gJnXAIef5sXTwMAg8tFZS4/wrOtoi+qs4SzPideZKTzzGlqn+juBGVfxNd31nDnqqqNNYvqVId3lqCLDSkQyJoYXzlHIsFb3uf5+ZlgFqQxLAh6sqtrYSC6iZZMIkgx7PFTfnLBJVFZqjiExMagqqdhYEmIlIjkOoZcZ0rbhABkGnCOSWuq2VGcjZAxahYwGocGMq3hx7G4Epl8F9DSyG9XM99MbeOR5YM5NwPAgcPgpYM4H6DEsexaYfQPj2WQ2qYGBQWTj8FMALFokDj8NiBieA8qfBWIT6R0uf45FtVMu4jIE7VJHX+Q6pI0qRIgqMqzchW4MEhZUK+YgybBWF7pxxhAOMgxoJHu0tdGYOgJaqR5BtGL2h3IXup6eMVVVLXsB4AiRdKKTnpYyHGQrZgklMiy3NQ6hN8pwBOKUqdD3MT/00JP0BCblAQceo1cwfSpw4HGgaDW9hAf/xgtkfAqw76/hHoWBgYEd7H0IyJ7HCMX9j7BuICEdOPgEawJiE0mYp1zMBJnyf9AWkZQDlK9n7nB+aNowS0QlGT5xwuYbxmjJXFXFwh2lSDKHyPCkSeQkSqkYo5AXbatHuMgwcJrPs7eX/1Ytq0eQJBLQbMk8CgnT9m4DQY9DqQtdAGXY46FabhsOKsPNzTYzn8cZg1ZMn0FoULCcdonDf2eo/tTLgAOPskhmzgd4MRzopjp8/BW2Yp3zAZLnwV5gzs3AwcdppzAwMIhctB4BqjYCCz4MVG/m7wtupy2isxqYdxtnidqPA3NvAVrKaZOYfQMw0MN6ghlX89wQQkQVGZ40iZXiwZJh7Yxhuc4gUVLiU3YDYgxlWIsMDw+HlwyP+Cy0OugB4VGGx+lCp02GhVC8IzsdBQVMRhkasvHiAGS4oEAxZMQhQi/TH+rrbbx4nAI6owxHMISHRLd8PdDXBsz7IFsxV78DzL2Z3uDyf3B5eJCq8cKPMJ90/yPAoo/RX2gK6QwMIht7H+LjgtuBfQ/RCjH7Bs7sxKcAM6/mMR07iTaKA4/y9fNuZqJEfydJcogRVWQYAKZMUSDD4xBJrVg1IOgCOgAoLVUcQ0sLiawfqqqo5CnFSHV0cD0OqKpFRdytMRKuTsUY0/NadhXAkUQMgGOoqxvVvXE6xlCGh4dJqLVsEpmZ/BCDQGEh90GJSI5BhrWtHg7YJACbCvc4NgmjDEc45t1Kf/Chp3gRjEkA9v8fs0STC7hcsILTq+/9id2q8pYAux/gazKmA3seDPcoDAwMxoJlkQyXrgOSC4H9j7IuICaBlqdZ17HD5IHHWDuQkMbXFK9lc54DjzFtZsqFId/1qCPDpaXA8eM2X+ykMtzY6FtnkFAiw9nZZDttbac8XVXFi75SZ2gH1W1JnGwpq2O0lQ7K9+wAGS4p4b/WFgkbQxnWLmR0iNAredCdJsMO2iQAm9+l2Fh6nMYYQ2Ii0wjPNAjiR0KIzUKInUKI20d5TawQolEIscHvJz5kO1m0BkifRlUoIQ2YcSWtDwAw/3Yqw90NwKI7gOpNQON+YNHHOYXauAdY+FGG9LceCdkuGxgYKODEBqDlMLDwY4xJ7GkEFnyIy32ttEic2MDEiPm38hhveI8zRQPdLJidcyNrCkKMqCPDUhm23Xijo+MUM+LgoGYkmYNEcvJkXss7O228eAxVNdzqtlKyxzhjAMLne5bfAVuWFafH4BAZlmOwHTcotz0C4SwCVI4bHCMvWSr0Sh0ZJw5uAzALwFkAzgfwH0KIkRr5ZAAvWZa1zu/HjlPbGQjBi96xV0h6593GyKWjLwGL/4X2iD1/ARZ+mBfD3Q+QJHviqBQv/hdGs23/Tch22cDAQAE7fsPGGXNvBnb8FkgpZirErj+wZmDqJcDuB1lMN/1Kb1Gs8NYNrAcGuvjeMCDqyHBpKafmx+jhcCpGmdqurKQaOGWK4oabmig7JSYqvvF0lJbysaLCxoudJMMOqttKyvA4Non0dMVIsp4edl5xgNBPnsxHpc9hBAnT9qk2NYWe0MfEjNrEpb+fvmPlMTQ308gf5DFRUEC3iO2i0jHIcHX1GW2RuBrAfRbRDuBvAEYGdU4FkCeEeF4I8aYQ4oNjrUwI8UkhxFYhxNaGhgbn9nL+bYA1BOx7hLnCSbnAe/cDOfM4VfreH5kuMeNqYM+fedGcfQOJcUI684ff+6MppDMwiDR0VAOH/g4svoOFckdfBJZ8AmivYK744k8A/e20Syz4MBATB+z+E3PHUwp5jKcUhbTrnD+ikgwDNm0Go7RklhYLLTLsAIkEFMcwSvGZZXEckszZRriU4fT0URugREIho9yPgEhL4xicUoYd+j7l5dE5YLsgcxQiKW0iWoTegTHExtL7rkSGRymg0/JuRxmEEBeNsDlsEEJsAJANwN/wUwNgZDZIN4ANIHG+GsCXhRDzR9uOZVn3WZa10rKslbm5uc4NIHchu9Dtuo+K78KPsjtVVx2w+E6g+QBQ9Taw5E6G8B96EljxORbd7f1fYMVnOd267yHn9snAwCB47PoDW60vvQvY+XtmCy+5k88LweU9f2HdwNJPMimms9pLmCtZPLfo42GxSABRSIYlibXlG45QMqykSI7it21tpcVCeQwOKsOZmUBCgkIDlIyMUZXhcJLhzEwgKcnm5+DxjEokq6p4nEvfq200NzsyBo+HBDAYMqzVQQ9wzK4C8GbCKMOBYVnWqyNsDussy1oHoA6nkt8C73P+791sWdb3LcsasiyrDcA/AawI2c5LLPkU0LgXqNrks0fsfhCYexMQnwrs/B2nVjNnAlv/Cyg+mx3stv6Ky/nLgG3/bdMrZ2Bg4DoGe73H7eVUd3f/iUWySblcnnEVc8N33sc84dxFJMnJ+d5ZoAdJpBffEbYhRB0Z1lJV/UiYJMNyPbbhQCtmiaIikhjdMcj3aRF6jyfo6n+ABFApXm2UvOSgfM8OEEkhgo+5q66mOhsXp7DhoSHe0ThEJJXGMAqR1LZ6OEiGS0oUyHBGxmlj6OjgDeJEV4bHwdMA/gUAhBBJAG4A8Lz/C4QQ50hrhBAiAcA6ADtCu5sA5t1C0rvrPiB7LlByHq0ScUlUhvY/SqV4xecZvVa9GVj5earGR18GVn6BZLr8uZDvuoGBwSjY82egqxZY/SUu9zRxFufg33gsL72LOcPNB4ClnwI6qnj8Lvo46wDe+xM70WVMD9sQoo4MZ2VRzQvGJpGfr2FzdFAZjovjRdvWGEZJMQiK0GdlBR3nJaGcNew3hoEBTmuHUxkGNIikE4S+pYWqVrjGEIFkuLg4uDGYWDU8AaBaCLEVwOsAfmxZVo0QYqkQ4v+8r9kP4AYhxBbQLnGfZVl7Qr6n8SmsMD/wKNDbAiz7NNBSxgKaFZ+jUrz918wWTkgHtv2SGcXJBcC797AIL30q8Pb3jTpsYBBuDA8Cm38KFK4GJl/AY1Qub/4pkDWXivHWe33FdTvv47G7+E7g+KtA21EuhxFRR4aFoCIajE1CWVGV63CIvAAK8WqxsfSrRpjVAwiODNfW8lgINxmePNmmTQLwZT77QSuFQf4fHCbDtnjBGGOIi9PYHYfJcGsrayMDIjMT6OriHZUXkgyfqcqwt3Dui16f7yrLsh72Pr/TsqwPepebLcu62fv3sy3Luj9sO7zkk5xafe9PrCRPLQG2/BzInAHMvo6V6MLDC+SBx4HuOmDVF9mdrnYbcNbXgJrNvJAaGBiEDwf+xrjDs77Gdsut5cCarzI1pn4XsObLQPNh4PAzwPL/B0AwdWLmNTzet/6SdorZ14d1GFFHhgEFIpmSQjI5QlVVJpHDwyQQDhJJJRI2wmJw4gSL+JXrWhy0egBU4XTJsHbDDReU4Zoam403RlGGKyuDsHo4aDHo6Rm1pux0yDH4MWfptVWaMLAsx3zPgO9/aMsqMUoXOvk9PIOV4ehC/lIG82/9JX9f8Xnmj9Zupw2it5nFNis/R1L8zk+AZXcBidnA23czxzSlCNj0/TAOwsDgDIc1DLzzI6q/s64FNv8EyJrtXf4pUyLm305VOCYeWP6vwN6/MH941b8DzYeYL77sM+xIF0ZMbDIsxCmNN4aH+T5lMtzayjc7rAxXVJzWWG50jCCSx4/z/cp5qi4ow+3tCnnJfuq2vBHQIsPJyazecwAlJbTw2mq8MUJV7eri7mgp9ICjhB6waTPIzGSWml/rQC1C39MD9PU5qgwDimTY77MwrZijEKu/BHRUsOvU0k/QR7zl5+w2V7iK060pRfQVvnc/EyVW/TsD/Bv3AKu/TAJt1GEDg/Bg/2NsmrH2P5kOUbedx2X9Ls7irPg8j9s9f2ZyTFIOsOUX7DQ5+XwWyMbE0yoVZkQlGZ4yhW10e3ttvNiPDNfX8/odbvICkMz29THfNSBGEEktQg9wHQ4qw8pZw62tZJ6IHKuHTPaw3XjDrzW2diGjwzYJSSRtk2HgFCJ54oSG/9xhdVuJDI/SPORM7j4XtZh+BVsvv3sPEJ9GS8T+R4H2E8Dab3K6de9DwNlfpwK1+SdUlhIygI3fo1KcOhnY8FXjHTYwCDWGBoC3vslkiHm3AG/8JwvgFn4U2PgdHqdLP0XP/2Avb2TLn6MavOqLrBfY/SAw/0NMlQgzopIMKydKeMmHNgGTkWQOEknlxhujKMNKsCyOw2FlGLBJwuR2vVPbx46Rl6WlKW7UYTKsrKoOD1MOh+/7F24iqTwG4CSRtCx+B5XHIL+PEaIMV1TwxuYM7T4XnRAeXhTrd1LdXfUFVpZv+iHjlvKXs0gutYQX2J33sUPV6i8ym7h2G3De3UDtVlatGxgYhA67H2Dh6/k/YLON+p3Aud+lOlz2LGd+hgeBbb8C5t5C+8Tb3wfSSlknsOO3wGAPsOrfwj0SAFFKhqd70zeO2GlR76cMB6VGynU5BKlI2i4E9JKP3l5O6SuPobubUrSDhH7qVD4eO2bjxSMi4o4d871fCQ6r25JI6nShC+r75PE4JmMWFpIEKrWV9o6hoYFfC+UGLg6T4dRU3hgFS4YNogwLbmdKxKbvA2mTqQ7v/hPQfhw459t+6vA32Lnu7bvpKU4pBF77MlMpchYCb3yDSpWBgYH7GOjm7EzR2ZzhefObQPZ8YN6tXE7MYTLM5p/yted8mzaKmneBs/+DSvGWX7Alc+6icI8GQJSS4Rkz+FhWZuPFOTknlV1J2iKBDCsTSe/0vCQ84Wy4IVFaSk6nQ4aPHw+CDDs4hqwsTq8rqareMZw4wX4iykVbzc1cl0MRd3FxbPqhowzLm4BwK8OAQrzaKAV0hgxHKWInsQr9xAbg+GvAWV+nYvz2D1htnr+MBDi1hFOuO++jz/jc7wHVm6gQr/sxFaodvw33aAwMzgxs/inQWcVjb/efgeaDwPnfByrfAo69zGN6sBvY/j9swZ49F3jr20DaFEYmbv8fFsme8+1wj+QkopIM5+ezhqq83MaL8/Iof1kWysvJjZUFORfIcGYmf2yNISeH0/PNzfoZwy6MIS6OyurRozZe7NdW2rJIoCMh4k423lBShv3IcHExA0uU4PAYAIWs4VEIPRCEMuzgOGx3oRvhGR4cpG/dkOEoxdJPASnFwFvfAlKLGbu2+wFmj573fcY27fw9L5xxScDrX+MFNXsel6dexp+3vsWAfwMDA/fQdoz+/bm3AHlLOStTvJYJEhu+ylmbZZ8G3vkxMNQPrP0WvcK1W1loN9jHQtnpVwJFq8M9mpPQJsNCiAQhxOeEEG8IIR5xcqcCb5vqsC1lOC+PV8vWVpSVATNnamywvp7Mz+HqnBkzbJJhmaHW0HBShVVWVV3wPQPAtGmKZLi5GU1NTGJQHsPQkOMRdwBvLJRyq/3U7Ugg9IAGGfYSSW3fs0vKsC0yPGkSf7xjqK7mvaIhw1GK2EnA2v/wU5W+DsTEUUmafgUw5WJg43cBTxwVp8NPs5Xzup+yGGfbr4BLfsXp2A1fC/doDAwmNl79EgABXPgzztp0N/D42/cIs7/P+wHQWc3GOQs/yizht74NpE/j7zt+zQ51EaQKA8Epw4MADgD4EYCQl63MnKlIJOvrUVYGzJqlsbGGBq7H4eqc6dPVyXBZGXm58oXfBWUYUCDDfkRSm9C3tjrauU3C9hjkjYT3xkIrhQFwtFmFhFS3AxbVp6fTnuH9PlRU0Cai/C9tamK8nXIrx7FRXEyF1xs4Mj78Yu6kqm/IcBRj0R0srHnzm1SWVn6BXuHabcCF9wA9zcCmHwAr/40q8qv/TqI842pWrsensLBuz4NA5dvhHo2BwcTE8VeBQ0/Qwz/Yw5zwxXcwZ3jDVxmZtuijwIavMDLt/O8D+/7Korpzv8sC2Hfv4bEbQaowEAQZtixryLKslwD0BHyxC5gxgwV0AXN68/IAAL0VDaioCEIZ9q7HScyYQXUxYMMHPzJcXk7yFhOjuDEXleHqahZhjQs5te1n9VAmwy4S+oYGG3nJksA2NmJoiEqsFhl2QRmeMgXo6Ditudzp8HhOKSo9cUIzhUESegdvEGXmc52dmW6/uEFDhicAYhOoFNW8y45zZ30NSMoj6c1bAiz8CBXgrjpg3U845brrD1Skhgf5urP/k97ilz5tiukMDJzGQA/w4qcYn7bqi8A/vwDEJjJNQnqIL/4voOINpkuc9TW2U3/96yTJC25nUkxPM3D+D8M9mtMQkAwLIS4SQmwY5afAzgaEEJ8UQmwVQmxtsBWqaw8zZ5KABZxW9RLJo/t6YFmaZFgqww5jxgwS4YARcSOUYVlAqARJJOU0uUOYNo1qZECbQUwMCbGfMhwJRYAAxwDYKASMjeX/r7HxZNe6SLFJ2B4DwG17/5dasWqAK+q2vDmybVkxZHhiYeFHSXylqnTe3UDlm7ywnv8DQMSQ9M6/DSi9kBfZuGTaKg48xoK6S/6bTQDe+XG4R2NgMLGw8bssVL38D4xOO7IeOPc7VIjf/Sk9xEVn8xhNnUzCvOUXQEclcNEvmB++7Zc8zvOXhns0pyEgGbYs61XLstaN8mOnZxcsy7rPsqyVlmWtzHWQUEpSG9A37FV0yw4MnvI+JbioDAM2IuK8aq5V36Dve25sJJFTrvYaH5LA2PYNNzXh2DHO1kux2DZcUoZlVJ9tq0Rjo77Xtq+PhmmHiaQkw7bHMEIZVoaDrZgllBJWRpDhtDSNzGqDyIInBrjoXsaqbbmX0685C4ENX2ZU0znfAg4/xfatl/6aU64bvgys+QqQORN48S5g6qXAvA/Sy9iwO9wjMjCYGKjdRnvD4jtZNPfKZ9klcsVnedx5Yukhfu+PQN0Ozt70tfKmdPYN7Db3+td5Q3t+ZLZQj8o0CUAhXs1LJMuO0lcQacowYMM3nJAApKWhsaIHHR2aY3BBjQQUSZi3eUhQGcOAa6qqrdxqLxnWVrddSGEANIhkYyP6++nRjRRlWO6HKhnWJvQGkYcpF7Iq/Z0fAt2NwMX3Mk1i80/YwSp7PvDyZ+kvXv0lYM9fgOp3gMvvZybxG9+gOjwpA1j/cVooDAwM9DE0ADz/L0ByHgnva19iLNrlf2DHyKMv0vbgieOsTuk63pBu+ArTJNb9BKjeDOz/Px6zqcXhHtGoiFoyXFICxMfbIMPx8UBGBsqqJiEzU+P63dNDM6kLynBxMXfPbkRc2TGquto2CYf9wgC70MXHKxTRNTfj8OEgCL1cj4PIzQWSktSUYfmZSSJtGy6R4cxMqu0qynBVFS0u2sqww2Q4OZmfhS0yLNVtyzIZwxMN637G+KXXvw5MvYRB/pt+wEin9/2WyvHbdzOmKX0a8PydQMFKtmre9iugaR9w6W+oZhm7hIFBcNj4HaB+F3DZb+nV3/0AZ2NSS4B//htQuAZY9hkuD/YAl/0OOP5PFsCe9TUeoy//K5vrrP5yuEczJoImw5ZlbbAs64NO7IwKYmJICg8etPHivDwcrk/XV4UBV5Rhj4dkym6iRFl1EoAgbBIuKMMeD9VRu8rwYFMbyss1Uz2ammjzcHg+XAhaJVTIcFkZb8iUwxQcbsXsj2nT1JTh8jJGT2jdXLlAhgEq3LbHMDgIdHQYMjzRkDWLKvCeB4ETr9NvGJvIwriS84BFH2dOaUsZcOUDVIRf/xpwwY9Z3LP+46xWn/dB4K3vMIbNwMBAHRVvAJt+BCz+F1od1n8cyJoDrP0mvcF9rcAVf6A6fOBRdpdLn8JjNXMmUyd2/o4k+qJ7gYTUcI9oTEStMgwACxYAe/faeGFuLva2FGP+fI2N1Nfz0QVlGCCxtZWXnJuLssYMCKFpMWhocEUZBkimDh+28cKsLBxvTMbgYBBkODvb8Yg7gERSxSZRXm4FV8jowo3J1KkKhL6/H+X7GAEiPdO20dPDH5fIsErmc3dlMxoaNAsZDSIX53yLitKLnwImZXKq9firVJvW/RSYlAU89xGg+Gy2fd3+P0yiuOJPtFW89kXgfb9ji+dnbgV6WwNv08DAwIfeFuDZD5HUXvxf9AZ31QLXPAyUr6dFac3XgLSpwEufYbzamq8yMaKljEpybwvw+je8Xv5bwj2icRH1ZLi8nNfl8dCaMRXV/Tl6ZNhFZRgA5s2juh0wWzU3F4fb81FaSguxEiyLpD4/X3c3x8XcucChQzZi7rKycLiNNxWzZ2tsyCXfM+DLGg6Y05uTA/T2ouywpafQu2STAHzKcMAxeLd9ZH8f4uNp11GCCw03JCQZtjuGo+91ANBUtw0iF3FJvJg2H6TVYcknvJXqXwCsIfoV63cBG+8GLvgRL9jrPw7kL+dU7M7fA8deAa55hNXsL95l40tlYGAAgMfKi3cBXTUkv4f+zsSWc78HpBQBL36ScWnnfIsKcfsJKsSt5TxeF3yIFqdX/x0Y6mPBqwsilpOIejJsWcCBA+O/bm/skpOvV4bLyvD8+QwYCKhK5uZiX+90zJ+vcUJvbwf6+10bw9y5QHe3jQ5oWVk4DDLIoJqfuIBp0xjyINPbxkRuLjqRjLp6T3C+Z5dsEt3dvvu3MeGdISg/PKSXWe0ioZ8yBejttZE1LAn9gX4AGuq2QeRj+vsYo/bOD9lp7or7gf5O4IVPADOvYUTTOz8CGvYAVz4IdFQAL3+G1eqFq1n0k1LA3w88ylxiAwODwNjxG5Lf8+5mksvL/48WpTVf5nE10A1c/RBw9AXgvfvpIS5cA/zjw8wWvvDnwJEXWDR39jdofYpwRD0ZBgJbJfYOUIZcMNdOa6sRkGTYJRIm1ep9+8Z/3VB2Hg5gDubPCNTdYhS4TOjnzuVjQP92VhYOYxZSk4f1dsVFMiyVxYB2j5wclGPGKe9RQkMDpf3kZI03jw/bMXdeIll+PFbfLwy4pgwDNnzDkgyX8+bQkOEJiovuZZbw+juArNlUgcueBXY/CFzyS6pUz30EyF8GrP0WbRT7/gq8/xEqJc/cxm52097HOKiqd8I9IgODyEbl2yyGm3kNsOLzwNM3AcIDXP0XzrgceZ6pEonZLF7NXczucm9/n53mLr+P7dSfv5PpL2u+Eu4R2UJUk+GZM1lPFZAMd01BMjpRmtKsvhFJXlLdMX7Pm8fHQGT4iDUNfZiEBcVt6hsJERkOpNAjOxuHMBuzSnr0ZkxcynsGFAi9HxkOKqbPJd8zYIMM5+TAAlBelahHIl1qfgJokOETsUhNdc09YxBuJOdxirV6E7tcrfw8MPkC4J+fpx/xyj/RSvHK55kuUbqOKtZgHy/K1ZuAN/4DuOavrH5/6kag01ZEvoHBmYfOWpLftCnAVX/hcZd9MNcAACAASURBVFa7jcs9zcCrX2Rx6rJPAy98kgV01zzERjebfsBOkbOvB175HP3FV/8FiJ0U7lHZQlST4fh4ek8DkuGmAszHPniaNDrg1de7Rl4ABiOUlAQmw/s6GcI6P9tOr9oRcJkM5+Ux1isgGc7KIhnOb1ffyOAgLQYujWHaNH6fAo4hJwdlXquHtjLskro9fTq/pnbU7SZko6M3Tm8Mkgy7MA5ZCBeQDGdmAkLgSE3iyXEbTFDMv9WbDPFt+oSvepDPP/cxdqI76+ucqj3wKHD1w1SSn74ZmPl+xq1t+Tmnc6//Oy/eT9/E/FMDAwMfhvqBZz7Im8zrn6BPeNcfeHxNPg946gNAUi6J8fbfsAHO+T8EMmbQHpFSCFz8S+Dgk5yhWfuf9BVHCaKaDAPAokXArl1j/92ygB3Hs7EIu32kUAUNDa4RMAk7qRh7G1n8Nj+1Qn0DLpNhIaisBiKSnQnZOIrpWJin8Tm4SMAAzjDMmgXs3x/ghTk5OIg5yE/t0kt4c/H7lJTExhUBCX1GBsqDJfSAK3JsSgr/PQHjBr3tvY80phmLxJmAS38NJOWxuj0pn401Kl5n3vB53wNKzmXyxEAnL9aNe4CX7mIs2+Tz6XMcHgQu/yNQ+Rbw0v8zBXUGBhKWBbz4aR5Tl98HWMP030+5iBaI5z5KT/61jzOt5dV/B2ZcDaz6AlXg5oOMORzq53GXv4wxa1GEqCfDq1axA9VYBTfHjgHNHXFYhS02KotGgVSGXcT8+SRh4yVK7K3KQAkqkNpRrb4Bl33PAMlwIIvB3npuf2G6BqGXn52LNyZ2CD3S07EXC7EgW3Oq1UVlGLA5hpgYlKWwN7w2GU5L04g1sYfZs+3lh1tZ2TjSnm3I8JmAxCxebJv2MVN44Uf4s/F7wIkNTI2ISaAiPPkC4JzvMPpp+695AU/MAf5+PTD1Yl6k37vfNOQwMJDY/FNg95+As/8TmHIx8MT7ecxc8wiw9V769C/8OX37T99MFfiqPwN7H2YL5rO/QeL83EeBvnbekMbEhXtUSoh6Mrx6NR+3bBn97/L5VdgSscrw4sWsoB+PAGw/kIhl2KFP6DMz6QNwCfPmAVVVQEvL2K/ZU5EOAFiUcEh9AyEg9PPmMdWjb5waRUt4sE/Mx/zkE3obCQEZPngwsOi1P34JYsSQfgMXlzKrAWDOHEb1BUJt+hz0DsUbMnymYNplLOjZ9itO4V76GyB7HvDs7YAnhhfg+l1UiM/5Jr2Lr32RfsYbngK664EnrycZnn8bWzfv+2u4R2VgEF4c+BtvMOd9kB3jnng/rRI3PstmGa9/HZh7M7DiX0l2O6t5g9lVRxV48gVUjzf/jHaki+8FcheGe1TKiHoyvHw5u6C9++7of9+6FYiPt7AIe9TJsMzndVkZDkToOzqAg4c8WBn3nj4ZdpnQL1vGx507x37N7r0eJKEb0/oCSZejwGWrB0AiOTQ0/hR9ZSXQYaViQbydLiMj0NPD/DYXv09z5nATVVXjv24f5mNmYpXe/ZHLhH72bM70tAWoFT0UzxOuyRg+g3DhTxmbtv7jzEC97nFaI565lWT53O8Ce/8X2HIvcOWfSZafvhlIyODvVRt5Qb/8fl9HrYo3wj0qA4PwoHIj8NyHmeF9xR95bNRuYxqLJ5Ye4rylbGbz1neB8n8AF/0cyFlA731cMotTqzezUHXOTcDSu8I9Ki1EPRlOTgYWLhybDG/eDCxZIhCfk6ZOhjs6SGBcalYhMWcOvZJjkeEdO8jLV2aWRzwZ3r597Nfs3g0sSDwCT72GxSAENgmZ7DGeb1h6uxcM71bfgMsNXAD7qRj7+mZgfpwGoQeoDLtM6IHA6vB+i4OVn5vBGYCYeODax6gEP3UTu9Rd9lt6HV/9Eot2Zt8IbPgKie8NT/N9f7uaTQDW/Qw4+Djw5jdZUJc+nUpY7TgnLgODiYi6ncDfrgLSSoEbn6bl6NATwIX3MDP4b1cD8SnAjc+QBL/9PbZCX/6vzPpu3EciHJtA0pw+hY03orSaOerJMACcfTawaRMDB/zR0wO88w5w/vkgoQ2Y5D8CtV7SVljoyH6OhZgYYMWKscnw1q18XFFUE7FkODeXqRg7doz+d8uiarw4s0L9cwA4hpgY2j1cwty5nGUYryBTkuH5vRoXzxCQYUkkx/MN9/cDZd2FmD+8R28jLrb2BnzdCQMR+v1905GMTkye7NquGEQi0qcAV/8vUL+TxTsLP+K1T/wSeO8BehlzF/ECPTxI0tt2BHjyWk71yoSJvQ8Bt7zIJgGPvY8XdwODMwHNh/mdj08FbnmZ/vrNP6Gqu+zT9Nd31wM3PENbxPqPsUj1st+y0c3+R4ALfsg0l2c/xNde+xiPpSjFhCDDl1zCJmubN5/6/MaNvPBffDGAoiKgWrH4rKaGjy6TYYCFgDt3cn9H4p13mBKQXxyrTyRdJsMA1eGxlOGyMvZqWDO5Ws+7XV9PAuZx7yublMRixm3bxn7N7t1AQWIbslsDxR2MghD4ngsLGYk9nrp9+DAwZMVgXu9O9Yp6y3LdJjFjBj/mgMpwRwnm4gDEgInJOuMw4ypfpNqO3wIX3QNMvRR46dNA/Q4qwp44Kl/Z8+gnrnyLF+6LfgHMuo6NBU68DtzyCpXmRy9lpbyBwURGeyW/69YwifDxV4HXvkSLwyW/BJ69DajaxGMmpZA3kUn5wHVP0BP8xn8A828H1nyVfuKjLwCX/CqqYtRGw4QgwxdfzIvniy+e+vwrrzAy69xzQZYgya1dhJAMr11LIvzOiAZJw8PAa68B69Z596NW0WLgcj6vP5YvpyLZ2Xn63+SNypo5rST0qiTMZQImsXw5yfBYu7dlC7CiuIZWAZ0xAK6OQwhgyZLxvduSKM8f2Mn+zSro6mKFoYtjiI9n7nMgZfhAcy7mYb+vxbXBmYXz7iYpfvmzJLXXPgpkTAP+fgMAiwVAndUkxDOuYjX8oSd44b/mr8CUC6l41e8iIR7sBf7vYqDteLhHZmDgDtorgEfWAb3NwM0vMBLt+Tt5I3n1/wIvfYb5wZf8Eph2KfD4lUB/B/CBZ9lE49nbgcJVwOV/APY9DLz7M2DZZ4Clnwr3yILGhCDDmZnAmjXAs8/6nrMs4IkngAsu8DaPk2RYhcCEkAxfeCFdAC+9dOrze/eSd114oXc/6utP94OMh6YmjjkEZHjtWm7q7bdP/9vmzfR3L5hv0b8yGmMeDyFSt1esIFcf7b6po4NEctWMFlbatbaqrTwEZBggod+5c+yovh07gNiYYczFAXUiKcfgok0CoA94vOztzk6goiXVkOEzGZ4YktrsuSzm6W7ktO5QP/D4VYyBuvZRtoh9+mZgxWeBlf/GNIrNP6F6XHQW8OytQPtx4OYXWUX/1/OBFo2ZHwODSEb7CRLh7gZ+17sbgadvAQpWAtc/CWz8DmPS1n4TWPIJ4Ilrgab9wHVPApOy6a1PSAeuf4o53s/fyY6PF/9XmAfmDCYEGQaA224jAZB+z61bOTV/663eFxQVAQMDahfO2lrKVC76VCUyMkjoX3751OclOT5JhmXChV2EIIVBYu1aKvGvvXb63956i6kZMYXe/VC1e4SQDAOjWyVkIeOqxX2+fVJBQwMQF8d2fS5i+XIKuGN1otu2DVgwuQOJ6PU1M7ELl5ufSCxdylmGnp7R/y7VbUOGz3AkpLHAR3iAJ64BkvPpEW4t48V7yiXAZb8DjjzPyLUL72ER0MbvMoP4pvVA3hLg7zdSLfvgq0B/Jwlxk42wawODaEDbMeCvFwA9TbRG9LbS/pA9D7jpOWDH75i7vfQu4Jxv0SpR8Tr990WrgcevAHqbeKxZw8CT19FCce3jUZcnPBYmFBlOSADuvZe///znVIRvvNH7AqnuqlglamqAgoKQVUdecQWn4U/4Rdg+9hi9uFOmQG8MknSGwGKQkkLCu2HD6buwcydw6aXwEVpVMhwim8TSpST0Y6nbALBytfewUbWsyMIzl79P4yV7WBZvFFcs6OUTOoQecP2zWLaMyvaeMWr8ZKHmEuxSJ/QTEEKIBPH/2zvv8Cir9A3fh4QUmqGFkgDSe68CSlGaIiiigkgREV11beu6+lvLKrq6a1l37SiKgAooCChVelV67zX03ns5vz+eGRMwgSSQqee+rrlm5psvk3Pm+5J5vvc87/sa84QxZrox5rs09jHGmDeNMb8ZYxYbY7r4epxZQlwpRbYObZRFIuEGaDsIts9W1LfaA9DoFVj2FUz+i5Z4K3ZWbdVl/RUly1deYvrYdrhvqhLvvmsCezOZZOpwBAr710gInz4MnSbByX3w4x1QoJKeL/sapv4VKtwLLT5Qd8a1P6q1crk7PRHilYoQx5WWMD5zVCsrObJ2hdCXhIwYzpcPnngCvv4aevWCIUP0PC7Os0PRorrPSBLdzp0+sUh46dJFYmXgQD1fu1Yl4+6917ND4cK6z4gI8wpn7/yzmGbNJOhTBuu80e2WLUkuU5cRMXz6tIrO+iAynDOnBH1q0e0pU1StIb6ipw1xgAr6ihV1YZhadDspScemdl2PIM/MHCDLbRI11CAvTe/zwoUQd90FSrLJiWFxDlgNvAmkdbV1H1AWaADcBPzdGOO7f3BZSbGb4NYvIWkK/NwVynWQ73HdSH25N3olueLE9P9TxKvcnUqiWz0UOk+BgtUkpvetgvumKdr87U1KvHM4gpEdc+GbRnDupITvsZ2qFFGginzyy/qrMU35u+UZnvwsLOmr5NRaj+lvaes0uLU/FLtREeEDa9TEJr6av2d3TQkZMQzw8stKNOvXTxUmXnwxxYuZjQz7UAyXLKlxf/CBqmO8+aZETffunh0yO4eUP5vFdOigiN7w4cnbhg3Tr69Zk8yJYR9FI700by5Bn7Lpw5kzMG2ajs/vc8hMZNgHgj57dlklUotuexM06zbJqQcZFcM+sklcf706PqclhhcsgFo1PaovM9VJQgxr7Xlr7QQgDWMJAG2BvlYcAX4Abk1tR2NMb2PMfGPM/L2ZKefoDyrfryS5NT/AxD+rhFqDF/TlPvVv6oxV809qPTu7D7QbDKXbKmloWX/oNFH1VX/qDDvnQpdZkKOgMu/X/ujv2TkcGWPjOBjcTD7f+2fDvhUSwgWryirxuxDuCLd/o7+RBf/VReNNr6syy5of9DdVqTP83C3ZOlGiub9nd80JKTGcKxdMnqzv9wkTICYmxYtBIIYB/vlPfbfXrg39+yu67Q0I//4gI3PYsUN+kVy5rvVQU6VmTdWJ/fprPd+9G0aPVtQ7WzaSRVRGBIxXdP7+QWQtzZurisfkycnbZs9W4YWbb0bLEJGRmRPDPhL03gj90aMXb58yRadDzUY5IDY2877n3Lmv3WBTIVs2RYdTi26fOQNLl0Ltutnk5w8jMWyMaW6MmZrKLT1/HPmBlCftTiDVqzNrbV9rbR1rbZ2CPjpnrwn1noH6z6nc2uw+cNMbynaf+zbMeBFafAjVHtRrv/4L7hwmMTDlLzD/v7JMFG+mTlxrh0sQx9eQp3jBh/6encORPpYPkO0nbzmdw+t/UpQ38Ub54hd/mkIIf6vVkvn/UZLpze/BL4/Dks91MVn3aZj4pJrVNHtHwjgEifT3AK41xqQRfIuNlWcivTaJ06dVGNdHAsxL3bowYIBEca9e0KdPihejoyXEMiqGfWSRAH3+jz0GTz4J48ZJCF+4oLkAElL582csIuk9Zj66MGncWC6AwYPhzju1bcgQ1SFu2RIptfj4zCUB+lAM//OfSlxs0yZ5+5QpqrASmd1krhGNt/ucD3z0DRvCO+8oGTBnzuTt3nrcdesCozJxHIIYa+1kYPIVd0yd3VwsfgsDoVdHrMlbcHw3zHxFUbEWH8CFszDnn6o93Lqvns98Gc6dUOvZsTm1/5mjKsk2uptKsB1JUhTtpy6KNh/eBE3/pVa1DkegYS/A9BfVGKN4M+jwoxLjfn1LnRnbDlSd4Pn/gUr3yf4w/e8w9x1dNN78Pkx6WheT9f6qi8lpz8PCD6HuM1DvL/6eYZYRXn/RGak17P2C9XFkGOD++3VLlYzWS/axGAbo3Rs+/hjatpVl4vHHkzujARkXYT72PWfPDp06wRdfSPvFxCiR8fbbU4iywoUzFhk+flxhWh+dTw0b6tpp3LhkMbxxo3zof/qTZ6fMiOEs7j6XkiZN4K231F3ylluSt3v93E2aoDmEUWT4KhkJPAhMNMbkADoALf07pCzAGCXJnTkqT7CJgFafKilu1qsSsm2+hMhYiYTTR6DNF5A9p0TByQNKwMtdTKLh6DYtI0//P5j3npLq2g+GmKyvMuRwpJszxxT9XTdCpdGavQu/PAYrBqoO8M3/hfG9FTWu/Wc1n5nwmGxENf+ki8Ypz6n0YJ2ndNE38xXZimr+SVHhECa8xHBGutD52GubbjLaeGPnTmjQIOvGkwoxMbKpvPEGJCTA889fskNmxLAxyV5dH/CnP0nQv/iiAtkHDsBTT6XYIaNz8FFrby85csCtt0rEv/eealgPHarXvNFuChWCzZsz9sa7d/tstaRRI4176tQ/iuFKlTwrQPHxly9IHOZ47BODrbVNgWHADcaY+YAF3rLWZrATUZAQkV0R35H3KKJrskkg2/Mw4yU4e0KtZaPyyEJx5ii06Qex+WWhOLZd7WXzFIfJzyjxqMOPSrKb8CgMqK9s+gIV/T1Th0ONYoa3h73LJHordoLvW6uiSuPXFNUdebfsEo1fgwZ/02rH6qGyQtz0ui4cF3wgr33z92DOG/pbqNZL9iIfVdXyF+ElhosU0bpxeti+Xfc+jqpekcKFYcaM9O1rrV8iw6D20Z99lsaLhQqpvld62blT0cjsvqtnWKmS/Nrve+qJd+16yTVF4cIyrqYX78WVD203990HP/4IY8cqOtyvnyLGJUp4dihU6I89zK/Erl2XhPmzjty5VdljzBh4/XVtO34cpk9PYbuJj7/Y3B3mWGunAlNTPN8FNPU8tkDornNeSkSUBO2IjoqQZYtQRDgiRsvIpw/pSz76OvmJTx+WgL7uehjXW5UkOo6GPMUUcfu6jmoYd56iqhMD6ydXpXA4/MXGcRK2F87pfM2dAAPqwYk9Ov8TGulc3rMYWnwEVbqrBvem8dD0baj7FIx5QBHjOk9D83fVlGbGS1C5K7T+TBeTIU7ozzAlRYumvwvd1q26L148a8eUUTLSSe/QITh1KjAFfUa6AfpJ0L/zDnz1FXz6qYTkRXiX5y9cSN+b+WGloV07VSh54QV47TU1oXn66RQ7FCok20NareouxVqJYR8K+rvvVk1hbwOR0aPViKNDB88O8fEK258967MxOYKIiCg1Bih9G4x/RN7HVp8mJ9n93E2Pb/lAUbPvmmrfjqPh0AYY2ADyllE2vomAb2+Ub7j7fNUm/rEDTHxKXe8cDl9y4TxMf0ktk3MnQvd5aik+qKE88fdNV13gAfXg4Fo1zCh/FwxuDpt/gdZfQO3HYcTdEsKNX5MQnvEiTHvB4yn+MiyEMISbGE5MVGJcekoFJSUp6S5//qwfV0YoUkTZQwcPXnlfHyeepZuEBIX4jhxJ3/5+qOoBWqLv0QMefjiVoHThwhJg6TkO4HObBKh54scfq1vba6/Jw/17ExqQGL5wIf0d3A4f1t+Pj8WwMfD553ret6+ui2680bOD1zoTLOW/HL4nMhruGKbaw5Oegpn/UJJdkzdh5TcStFUfkA1i73IJ4DzFoMtMT+H3G1Rbtfs8tW/+uSvM+w90nppcu/ibxnBok58n6ggbju+GoS1hzus6d7vMVPWHH+9UV7luc+V1//ZGrYh0mQV5Ssjes2+5mtRUuAd+uF0e45v/Cw3/DhOfUKJp9YfgtgFhlSgaXmLYG+VN2eItLbZuhWLFAs8nk5EScT5OPEs3iYm691pRroSfxPBlyWi95J07VY7NxxdXrVurPNkPP6je80Wnc0a7Afq4xB3oVOncGT78EF59FSZNknc7IsKzg3cOLonOcTkio6H9EKjaE2a/pi/9+s/JN7xxjCLCReqr2ca5k4qundyvCHDh2jCqk5Lr7h6r5KP5/4Eht6js1B3D4MBa6F8TVg3x90wdoc76n+DLqvIDt/lSft8fbkuuCNF5Giz+LLm5Rtff5Hkf1AgunFHEuFBtXcAlTVFFiVqPyiqx8EOo+xdo9ZlEdBgRXmLYa5bcko5qQklJEsOBRkKC7tMjJL2R4UATw945bNt25X3Pn5dYCzQxnNFugLt2SUBn8/2fXPXqighHRV3yQkYFvR/EMKiiRN688I9/QP368nL/TmbEcIMG8o44wotskaoaUe9Zfen/3FU1hzuMULvZgfVVYaLrr5ArAYa0VIJRp0nJzTqGtYdG/4B2Q2DfSviqhpaReyySbWJUJxjVWRUpHI5ryZljMO5h+X1zJUC3+Urw7F8Tdi9QBZTGr6pL3Ow+UKWHVi/WDpdYvu56CWOTTef64U2yA1W4W756r1Wi2duBFwT0AU4Mp8XWrYHnF4aMzSFQbRIZiQzv2ydBHGiCPjOR4UA7DkEihosVg2XLVKFk6lSVjPudjM7BWiU+Oo9xeGIMNP23xyLxrTLuExvDfTPksxzUSFHerrPlHZ70JIztpTJVrfoqkvZVDSUp9VgIeUsrAjf/fYnmG/uoa9eXVZTY5HBcC7b/KtG75HOo/zdFd5d9pdWJ6LzQdS7kKwdf14atU3WutvxYXeR+eQxKtZaVYs8S+OZG+d/vnwWFamhVZN0ouOV/0OilsBTCEG5iOC5OKepXEpJnz0q8BGJkuGhRRRfTY/VISlJILWXHgkDAK2zTExkOVEGf0ciwE8NXRb580KLFJV0lIeOR4aNHlYHnhzk4AgRjoMHzqgSxdQYMbAgxcYqaXVdCCUnL+stD3Pg1WDEIvmkEJVtKQERkh2+bwOohEhi1n1Rt1gH1oGRrvU9MPvi+DYx9CE6lM6/A4biUM8fU/W1QQyVpdp6iCg/fNIZ578oW0X2+EuK+aQwY+YOvv0U/s/xraPSKygAu/kzl1/JXgG6/gYmUP37vcp3rtf/s79n6lfASw8Yo2nslIbl9uyJIgRgZjoyUzSC9Yvj3OloBRHS0upilJzIcqPWe4+I0j/Q2QPFxFYZ0ERcn70RGxHBUlH4uUMiTJ+NzgMA7Fg7fU6UbdJqoElQD6sORrRK3Zdoq0e7nrqrPetcoOLhBUbfjuxURLt9Rnbt+uF3C+p7xat4xsAGsGwn3z5EnedlX8EVFWDk4/dVzHA6ADWOhX2VP7d/H4IElsHuh5zzcBR1/hoYvwoi7YPLTULIV9FgAJ/dpn8ObtU+9Z2XdmfpXJZF2nqaE0EEN5Y+/bxqUbe/v2fqd8BLDIHF4pciwt6xaIEaGIX2CHjTPQBTDIEGfnshwoNZ7NkZ2D++5cjnOnVPkMtAEvbd3eUaEZOHCgbWM5m3Gkt7IsBPDjpQUu0ke4Zi8Kjm1bqQy7W96A1Z+J8GQv6Kib7mLwbDbYcYriiq3/hy2z1Iy0+nD8OByqNxFCXrfNYGKnfVzeYrDT50VcXYVJxxX4ugOGHUf/HCruiJ2makOckNbqwFMyZbQc6lKq31ZDbZOVyJo++9hzptakchTXOde3rK60Fs7TPag9kNheX8Y0gJyFdG5X6Suv2ccEDgxnBpeoRmoYrhEiSuLYWs1z0CMboOEZHoiw0lJKh3gTboLJBIT0yfo9+7V8Qg0MQzJtbfTQyBGt0GC3olhR2bJVxa6zoGEG2B0Ny1L13tWlSOOblWzjQOrJRy8pdQG3SAh3X2+EpNG3qM6xs3fU2OOo9v1cysGwb0T5cfcPhP6VVJt2DPH/D1rR6Bx7jT8+i/4vJzEa8OXZbnZNB7611Ld69u/Vcmz6S/K8pA7EbovgOJNdU7Oe1fJnvfPVje6r+vCid1wzwR1lhvzAPzyuMfOM0fnrgMIVzF84AAcu8w/ow0bFHEqWdJ348oIxYsrInm5hg+HD8sfGeyR4S1btG9kANY7LFYsfZFh7zwDLboN6T8OENhi2NkkHFdDbH649xeVlVr4IXzbFApWkdCIK6kM/ql/haZvwV0/wZEkCZRtMyU8buyjrP1+lZWt32sVVOspcdKvikTHg6u0TD3ndfi8PCwfCDadTXscoc2G0Uq6nPa8/L4ProTiTVT1YfZrqgncaxVE5dI5tuxL2XC6/qrVia9r65zsMFLJnlP+qsTOfGV1Ducrq5rDy79WNZS7RqrzouN3wlMMw+Wjwxs2KOr3h2ydAKF4cSX5XS55yzu/QBXDiYmqFHH69OX3S0oK3Oh2sWKKbl+pg1ugdjOE9Ee3QRFkb9JdIFG0aHKi5ZXYuVMdVPLly9oxOYKPbJHQ/B0tJe9dKrF7JEn+3zpPybs5oD7ElZJ/s2gDGP+wylZV6aamHDkLK2I3/mElLnWZKdExrB1MfFwJeffPVjWK0d3U0CNpmr9n7vAXO+fB4Fvgh7ZKaLtnvFYRpj0Pg29WR7mOo+Hm/6g29rB2unDr+hvU+rP8wuMegqI3wANLdW4OqAeLPtaFXZdZsH+1Z3VjncRy41fCpqtcRgi/T8Qb7d2wIe191q+H0qV9M57M4BW4l7NKBLoY9toeriRiAlkMJyYm+4Evh/c4BeI8EhPVCfDo0cvvd+aM5hmIdpWEBEWG01MuzY/1nh1BQoW71cHL6yP+9S3VXu04Go7vlLDY8DPcO0Feze2zFf3dOU8i5cbX9foXFbSt21x1vNs8Ucl0a4dL9Nz2tbqEfdcUhrSCnfP9PXOHr9i/Gn7sKOG6d6k6wHWbCzvnwucVdP40fg16LpPl5ouKKtnX+FXoNk8l0vpVhi2Tofl/dD6tHwkD6ioh9O6x0OSfMOMllQ/MUUjvX7adv2cesITfN0L58rpfuzbtfdavhzJlfDOezJCeTnqBLoa9c9i8Oe19zp9XVDVQ5+D1lF/J72UjJAAAIABJREFUKpGUBDlyqMxdoJHems/e1wPRR5+QIE92esrcBarVwxFYFKgk8VCpC8z6h2wTBSopIpzYWP7goW2g9K0SLIXrKEI37HaoeC88uAISGivLf1BDKNYEeq9TWay578omcfYE9FoNzd5R04QBddUaeu9yf8/ekVUcXA9jHpSQ3Txe4vahtRCVW37yGS9BqVt1XpRspQul8b0hfyVVManSXefYuF5QqKbOvfIdlDQ34VGdZz2XqubwN41h7ttQ4xGdy/nL+3v2AU34ieG4OHkM16xJ/fWjRxUBC2Qx7BWHGzemvc+WLbJ5FCzomzFllFKldL/pMtnVu3Yp8hqIEVVIvxgO1NbekCyGr2SVCOQKKxnpyrhzpxPDjvQRnQfaDoDbv1Ey0pfVZWm4Zxy0+EhezX5VVOP13l+gxYew41dtWz5QtVvbf69I3aAbYPJfoNHLSrrLX0kNEb6uDbmKQu/1EkabJ6k6xfA71GjBERrsXQ4/ddFF0KpvofYT8PBGiK+hRi9je6q6Q6fJapYxu4/8wse26/y79xdFi/tVgh1ztE+nSbBlooT19tnadvcYrUB8VUO2iDt+gFafQPZYf38CAU/4iWGAcuXSFsNe+0Qgi+HcufWFvm5d2vusW6c5BKIAA4mqiIjLC/pAthdA+oVkIFs90tsa2/u6d86BREbE8LZtgSnoHYFLpfvggcVQoLJKpP3cTdFfb0R4/MMwtFVyRK/sHYomf1lVgrrXarjhRVj3o8TQmh9Uu7jDSLV//uk+dQUrWBUe2Siv8dbpEtDfNYON412N4mDEWtg+B4bfqXNh3Uj5eB/eBKXa6IJneHuw53TR1GkybJsBfUsr0a3eszp3YgvCV9Vh2guKFvdcrmoQQ1tphaJIPZX1K9dBbZV/vl/n0gOLofxd/v4UgobwFMPly6dtk/BuD2QxDBL0l7N6rF2rfQKVyEhFuK8U3YbAtUnkz6/oe3ojw4FIeoVkKESGT5yA/fsDU9A7Apu4ktBluqK3q4fAF5XUAKHTRPmGd/7myfL/Sl7geyYARoJlTHcl2D20Vs06fn0T+paFI1tUDaDdYLWC/rGD6r8WqAyPbFKZtgPr5Pn8qjos7gtnjvv7k3BcifNn1Op7YH1ZZJKmqkzaI5tVjm94e50Xh7dAq0+hx2I1yuhbBma+Ate3lOCt/WcY+yAMbQn2PHQcA7d/Byu/0bm28zf9/L0TYYfn/NswBpr+S+2arwvQ780AJXzF8O7dKj92KcuWKWJZPsD9NZcTw+fPK8Jdtqxvx5RRSpW6vBj2vhaoYtjbeONyUdUzZ2T3CNTIcEwMFCiQPptEXBzkyuWbcWWEAgXUhe5Kc/CKZSeGHZkhW6TH5rBA9V1HdISR90K5O1UKq1QbmPEifFVN/xt6LlUy3aYJWt6e+64qBXT9TS1xJz6hmrKnDkKPRXDrV6o/PPIeJellzwm9VkKbfsr+H/8wfJwou8XByySAO/zD0R0w+3X49HpZIk4flnXmkU0q0zekhfy+J/ZAq8+g91rIngv615BlJm9ZVRpp0w+W9oO+5VRy7cbXtQoRkV3n1vS/61x7cIVWIUbeA6M6QVxpnUf1n4NsEf7+NIKO8BXDAKtW/fG15cslIgO1rJqXcuXkbT506I+vbdmizPpAjgyDxPDlPMNr16psViAKMC8lSlx+Dt7W3oEYUfWSnvJq27YFrog0RufJlSLD3jkG8rFwBD7x1aDbb3DTP2H9KEWJN/8Cd3yvLP4L5yV8RneHKl3lB676ACz8AD4rrdrE94yXDzR3ooRQv0qqOdxzqZbMo+Mkfj8vr9a79/4CXWZomXzB/xRZHnwLrPhGiXgO/3D+rOwPw9rBJ8WVAFewmqK498+BsycV1R95D5w9rgueB1dCRLR8vT/fD9miZJm5d6I855+VhrnvQMVO8NBqJc2N7qFz6sJ5nWPth0oof15B52CTN+H+WVCgor8/kaAlPMVw9eq6X7z4j68tWwZVq/p2PJnBK3RT8w17I8bBIIb37Em7Acq6dYEf3S5T5vJl+rxCOVCj25C+xhuBbPUAzSG9Vo9AFfWO4CFbJNzwgpa481fUcvagRpAjXv7Nxq9KJPUtp451zd5Ork085S/wWRk4uA46T5Vwis2v9+hbVrWNO01WglTBqooEfpwom0Tdp7Xc3ugVdST7+X74sAiMe1j+VOctznqshd2LYcpz8EkxeX93zoP6f5UV5ub3YeMYieOpf1Xt3w4jFLU9f1Z2hjE9FPm/czj0WAAn96sU3+Rn5EPvsVCrCIs/g8/LwroRapbx4HKdY4NuUPWIwrV0XjV4XuekI9OEpxguXlxF9xcsuHj78eNamg8mMZxaIqB3W6ALSW9FibSsEsEihvfvh4MHU399/XrdB/I8ihe/covyQE88S097b6/gD8RayY7gpEBFeYlv7Q+HNqo82pRn5fd8aI3HI/yWxG/SVCXO3TtRHekmPCrxe3Srlsc7joa8ZSSWPymmqgC3DVAksXpvCaKBDTxteBOUINVpMpRtDysGyp/6aUl1H9s5zwnja82+VTDzH6r5278mzHsPitTXMX1oDeSroKoQX1SEJX2h/N0SwO0Gw+5F8FlJlUmLza+f6fYbnDyg6O7Ynqprfc946PizqkP0LQNz/qnEuIdWQ50ndGwH1NUF0+3f6FzKX8Hfn0xIEJ5i2BioXfuPYnjxYv0D8UaOA5nSpdVJa3kqNSmXLFH5uPh4348rI3gFYmqC/tAh2Ls3sEUkJCdaphUdXr8eoqMDOxpZqpTEfFqC/sQJRfAD1fcMyZHhywmAbduU9Jgjh+/G5Qh9TDao2l2CqNZjsOgT2Rs2jNayePf5ivBO/LOigif2wH3TJHxyJ8gO0becxPRdP8tTXOIWiehPS8CcN6BiZ3h0u0q6nT2pmsYfFpG3tEo3eGyHfleByjD/v2rm8FkpiaekaYpIOjKGvaDydtP/Dl9Wk5Vl1msqhdfqU3h8JzR4ATaOhY+LKdp7Yg80/Tf8KQnqPaOuhZ+UgFmvSjh3miS7y7FdOkfG9UohjufBqUOqPPHLYyq/122ejuu6kbqgWvgR1PyTqkxUui9wq0UFIeEphgFq1ZKQTNkOePZs3d9wg3/GlBGioqBKFVi48I+vLVkiQR/ofygVKqgTWGqC3mv/CHSrh1cMeyPAl7JunS5cArnjmbfbYlqC3hu5D+SujImJcPIkHDiQ9j6B7Ht2BD8xcVra7r5A1olfHoMvq3hsD5MU8YuIVim1flW0NN5lpmwSuYpKLH9SXPVkW34scV3jEVj/E3zTCL69UUvh3X5TFYqqPSS4h7SQWNu/SvaMx3dJQOWvJGH8XVP4oCCMuAeWfQ3Hd/v7kwpcTu6HNcNgTE9dbAy6AX79l6K2N78Pj27TMT6SpNbcg25QBZGy7XSB030hxBbwlFOrBqu+g2o9JV5v66+I76fXK0KcI16rAV1/TfYWj7pXF1cdRkLnKVo16FcZJj2lJhs9FiopLybO359UyBG+JpMGDZRkNncu3Hijts2erUhkoDaquJRatWDECEXDvML37FmJyyef9O/Y0kNMjMRkamJ45UrdB3pVD6/VIy0xHOjdDOFiMVynzh9f94rkQBbDKZu45M+f+j5btzox7Mh6CtWQF3jDaJj6nEqmJTSEpm9DzyUSW7NelSie3Udlt7rMUPLU3LdVkWDu20qcqvU43PSGSnUt/EhR5CnPagm+Sjdo9q7E8vKvtWz/278hTwnZMxq9DO2+gy2TNJaNY2DN9xpjgcpQvCkUawrFm0COIPnOu9acPqravlsmQ9JkeYGxEH2dKjaUuV01fY9sgXWjVBJt33IJ1hK3QMOXVE3k0EZY+gX8cDucOSLLRLN3tWJwcj/M+4+O0bmTet+6z0DxZmrN/VV12LdCF1C3f6d24Dt+hW+baGz5K0o0l2oT+AGuIOaqxLAx5g2gGZAdGGWt7XNNRuULmjZVCbUJEySGz52D6dOhXRD17q5VC/r1u9jPuWqVynkFg9UDFN1Oy+oRExP4NokcObREn5oYvnBBQrJlS9+PKyN4hWRakeFgEsMbN6Yu6K3Va40a+XZcjvDEGCjTFkq1hqVfwcyXFd0t1UbJbz2XphDFnWHG36HO09D2Gzi6TcJ2WX8lUCU21tJ4t7mwaz4s+QLWDIVlX8p7XLkr3PJfiMmnygJrflDFiXnvqqtZydZqCNLsHTi8CTaNl395WX8JbFAUuWh9NXAoUle2jogo/31+WYG9APvXSGh6b/uWa3tElC5YGr8KJZpDfHXYNkuf59S/6ZhgILGRIrPl74YzRxX5HdRQUfmIaKhwD1R/SJ/lulEwqrMqjUREQ+X7dYzjSsLyAfKMH1x3sQjeOQ++vxU2T1DkuOUnUL2XS47zAZn+hI0xtwGFrbUNjTERwCxjzEhr7dJrN7wsJC4O6teHsWOhTx+YNUtLrG3b+ntk6adWLd3PnZsshmfO1H0wWD1AYnjECDh16uJydkuX6rXIIPgnUKZM6jWft23T0n2gC/pcuaBQocv7nvPmVdJpoFKypO7TSsY8cACOHAlsQe8IPbJFQo2H5O9c+IFKZg1soBJpXlG89kdtn/hnieaaj0qUNfmnRxB/qrq1OZ6Cqj1VOaDFh+pot3yAIsmz+6i1b/m7FIFuO0gR4w0/K/q47CswERJz17eEhi9CfE21md46VR3v1v+k/UDiLb6GRHHBKookF6gCOQsFR3Ty1CEJ3b3LYM9S3e9dKgELivwWqa/kw2I3qcrH/lWKos/8B2yfCedOQfYcOlY39tEFxbmTSmQc1k5NL0A/X+dJCeTTh2HJ5zDybtlRcheDxq9Bjd6A0cXHoo8ULS5SF9oN0THbvVA1iDeOVZS+6du6AIrK6acPMPzItNKw1o42xkxMsSkbcOrqh+RD7roL/vIXCa8BAyA2Flq18veo0k+tWpAzJ0yapLmAotsJCcniINCpUkUR1OXLkyN61ioyfMcd/h1beqlSRefPhQsXe4OXeq4Lg6E6SenSl48MB7qIzJVLCaNpieFgiG47QpeonBKxtR6HRR/Db28ronh9C22/f7ZKo817RxUE5r6tKGONR1RObfMkWPyJRPNv/1IEt0o3uP1bibbVQxRpnvGSbvkrSWTVfQbaDoSdc9WdbOMYNQYBiIyBojdAsSZQ769QuDacOgA75sKueYpCrxuh5X8vMflU8SKuFFxXUre4UqqXnLOQRKYvxPLpo3BsBxzfCUe2qszcoQ1wcL3uT+xN3jf6OtX+rdxVArRoA8iVALsX6DNf8D8YcTec9tTsL1hVn/v1LWRlOLBaCWxDW8EeTznW+Orq9FaxE0TlhtU/yA6zdbrmX/o2qPGwovK75sPU5xVFPn8ayrRTq+XExqoY8n0bRY9j8kGTt5SEGRXAtfVDlCuKYWNMc+DlVF7qZK3dZYxJAPoCfa21fwiPGWN6A70BigdaNnqPHvDSS9CliyoaPPhgYDd4uJSoKGjSBCZ6rknOn4cpU+Dmm4Pj6h0UnQeYMydZDCclwb59UKOG/8aVEapXh6NHYfPm5OV6UM1qkFgOdEqXhsmTU39t/XqoW9e348kMl+to6N2e8vg4HL4mKpc6hNX0VJ2Y+zYMvllR2LrPqAzX4S2qTbx8AKwYpIhszUeUFHf2hPzDKwbCL48rsarUrao2cc84RT7XDpcwnvOGIsax+RUNLtVGEUwTIS9q0jTYOk1WDSxgIF95KFJHtW7L3qGo8LnTirLuW6HbwQ1azl/zA1w4d/H8IqIlinMWViJZdB6IyiPBGJ1HHdcismsM2SJ1MxF6nwtn1Mr4/FmJxrPHFGk9dUhC9dQhtS0+vlOd+i7CSJDnLQNl2uu+YBWJ4Og4T2R4iawR8/+r5/a8fjRfeV04lLhZFgkToQjx2h/VEOVIkt4/oaEqRZRtr4jvhtEw8UldYJw/o/dp/KoSG6Pj1Db56zoS0FG5tL3O07p4WD0U+tfSazkLq2lGzccgOndWn4GONLiiGLbWTgZS/ZY0xjQFngWesdamUh8LrLV9kVimTp06gVX4MF8++PBDeOghiYE+wWN5/p02bWDMGEUhDxxQCaxgiaiCynUlJsqm8uc/a9uMGbr3JjYGOimbuKQUW0uXwvXXw3XX+WVYGaJiRRg4UC3KU473+HElpfXo4behpZtSpXRRlRreyLATw45AICon1H8Waj+uLnLz3oPR3WDa81D7CS2tN3kLVg2WTeKXx5WMV/4edbWr85SE6YqBEl3rR8n3en0LKHcX3DlMK2ybf9HS+6ZxikyCIp/FboLEm6DB3yAyViJx13yJ3C2TJMK95EqAApVklShUGyrcK99rziLqjndooydKu0vWgJT3B9dJoJ85kvFOedmyq2pC9HUSl9FxkKcY5LpNXuhcRTWG3AlKGjx1QL/v4HrdL/lC1ohDKS6Qo6+T0G/wAiTcIG8vKEK8dbouTnYvSt63RHPZWUq3lXDfMBqmvaDP8+wJCdmaj0KlLmqAsXWGyq+tHizBHl9dvt9KXSTwl30FCz+UwM5fUa2XK3WByOjMn0uOa4KxmSzMbYypAPwb6GitPZOen6lTp46dP39+pn5flnLwIOTOHRz+1EvZt0+2iK5d1fxhyhTVW80ZRF6jTp3kdd66VRHt3r3h++81n0AuSeblxAmdPy++CK++mry9UiX5iUeN8t/Y0svo0fLLz5x5cZLZvHlQrx4MHw533um/8aWHl16CN9+UTzt79otf69lT+QE7d17VrzDGLLDWppKhF7oE7P/tUMJaJbbNfRe2TJSFofzdWmpPaAi7FiiZbvVQCctcCfIhV75fInXHr4oGrx2uygcmQsvwpVprqb5gVUUhN45TNHj7bLUHBshbFhIaySZRuI4E3KmDshHsWynRvX+lPLUpBa2JUDQ2rqTucxSCnPG6zxEv72u0JyqcPZfmdO6kJwrsuVnPfbbsEvMRUWpPHOH5+z19WGNJeTuxB45ulwA/tgOObZdV4tzJ5LFFRMF1pTTv+GqaU8FqEtH7V8s2sn22bgc8cbxs2eWpLnELXH+LPo8Da3VBsX6UIun2vER42fZQ9k4o0Uz7rBiki5IjSeosV76jrBZF6+vYLPpEx+78aY8t5VkofauqUjiylPT+z74a9dcLKA1MMMlL8u9Za4Pgm/8S8ub19wgyT4EC8Oij8P77et6nT3AJYYAWLWDIENVMrllTwqxZs+AQwqCKEuXLQ0rBcOCAKnt06eK/cWWEatV0v3TpxWLYW+kjGKweZcrIKrRx4x9L8q1bF/gl7hzhizESrqVaK+Fr8WeK+q4YKLFbvTc0+7dq3K7/CVYOgvn/USSzQBV1KavaHZq/q8jm2mHJUcxpL8i6cH1LJYNV6a7nuxfJLrF1mpb6l/f3jCVCkeBCtfW7K94rD3KeYh5/7kY4vNlz26T7rTPgxG75l9OepCLi2aIgW4R+j8mme5BQ9N7OnUbWjTSIiNIFQa6ispiUbitrRN6yus+dCMf3SOjuXQprhsOMlyXqz3tid7EFFB2u2kMXHIXrKJq7ZRIs+lQi+Jinq2W+CrK3lL1DNpJ9q5TAOO1v+hxNBJRsKbtDmfayfKwaAhMegT1LdEFQvZcEcsEg+F8ahlxNAt2zyCLh8DdvvSXLR3S0EgKDjTvugEcege++k/d2xw7o2NHfo8oYN90E336rEn2RkcnL9Y0b+3dc6SUxURVWvD5nL8uXK7E0GOwFXsG+fPnFYthabevUyT/jcjgyQnw1aPmR/KmrBsOSz2DSk7JJlG4LlbtA++9lP1g9RKJrdh+Y/ZoS2srdqVvj1xRF3TRBy/obx0hcg0qyJd6oW9N/y+96dJsi0LsWyDKxaWyyQAbZKfJXgLjS+vk8JaBoPd3nKSYbw5lj+p3Hd8PJvR6LxDHPved24SxcOK+SZva8HoOsAhEpbpHRes+YODW9iM6rxzkLKdns1EGN+eh23R/ZDFumeKwS65Ij36Cfia8hwRpfQ1HfvGXgwDrYPkvNSMb1To4Sx+T1RIhbQMkWkKe4EgvXDoOf79f7YySmb35fiXQxeWVJGd1NVTzOn1FEutWnskK4pLiAJtM2iczgltscadKpE/z0E5QoIXvEpk3B1TZ3yBDN4ddflRT47LPwv/+prXSwzKNJE4n5WbMu3nbqFPz2m//GlV5OntSqyCuv6OZl+3aJ/Q8/hMceu6pfEag2CWNMNPAw0BHYbq3tnMZ+a4CUXpFu1tqky723+78dAOxeJL/pqiESm9FxWoqv3EX+3xP7tJS/drgim+fPJAu6ki11y5Ugq8TWGYoIb5uRXHUhOk6e10Kem1csnjoke8T+VbJM7F8FhzfKDnBpFDhbdlkjvBaJHAX1vtlzSghmz6XIcGRsclQY44kOG4nkc6c8keFTup09JtF78oDHJnFAt2M7/vj7TYQsG3nLKUKcr6weF6wq+8ahjfoc9yzW/c55SsgDieuEhh6bxM36DI7v0oXE5gmKEp/cL99w8ea62CjbXnPdPkvHZfUQ7ZMjXgmNVbqpa1ywJLOHKL6wSTgc144334Rp01TVY9Cg4BGQXry2jlGj5LEdMUJVPYJpHvXqwQcfJNd89nZofOQRf48sfcTGpt7RcMUK3Veu7Psx+Y5zwGrgTaB7ajsYYyKB3dbapj4cl+NaUKimbs3fUzmuld8oIW7pF4p6lmmnJfw7h0sIbxwrD/KmCcld5/KVlxc28UbZLXIVVYRz6wyVUtu9EBZ8IDEKErD5KiganK+CPMjVe6kaQkS0RPnhzap+cXSrhPWJvdp+Yo8S2c4cUWTY+54ZxWSTqI/Jp1tsAQndXEWVOJc7USI/T6KS6ewFlVY7sBYOrlVkfdarF9cYzhYp20fpthK/CY0gf3lFs7fNUkLjmAfklQYlyZW+TRaTUreq9vCWKapHvG6E5hoRrc+/SlfZUSKypzUjR4DixLAjMChZUiW8jh1TA4hgIz5eNaoHDFAVjA0b4P/+z9+jyhhNm8I77yi63bQpLFokYdywob9Hln6qVPmj1cP7PITFsLX2PMrfaHqZ3YoBMcaYkUA+4Adr7X9T2zGgS2KGM9kik73FZ44rGrxuhITxks8lYEu2UdSyyVuqVrB/lccqMf7irnPXXS+Bm9BInuQClSU+96+EXQsVQd2/SoljKatLgAR4nhKyD3htEvHVFQ2OLZB8762ScOGcbAtnjsO5E7Iu2Qu64XmcLbuS7Ly3iBh5g42BsycVET65X/cn9skaseM3CfGj2+RnPrbd857ecRaGfOXkk46voQuKApU0z30rFR3+7S2J4EOeijORsfpMqvSAUq3kyfbaTX55TPWaTx9SxLv0bareUaqNK4sW5Dgx7AgccuYMvuS/lDzzjJIB27SBokXhvvv8PaKM0bixotuTJ0sMjx+v7cFS4g5U5m7kSHWby5NH27wdGgsW9O/YrgFXqvt+hR/PBkwDXkLZSSOMMautteMv3TGgS2I6RFROqNRZt3OnYctkCeP1I5OjwfE15Hu9voUqU2SLVELX9lmwbaaW/71CN1t2T/k0TxS6wt2KCOcooOjugTUSx4c2qWLFkSRFXDf8nHbiXGSsRGP2HBffmwiPfcBzM0YC+dzJP95OH7m4UsSl7587UWK8RDMJ83zlPbeyKo926qAqSOxZrKoOexapzrA3kS5HQU/L60cVKS5UU9u3z4GV38lv7S23FltAFxrl79JnGhmT+rgcQYfzDDsc15L331fd59dfl+0g2LjpJtWqXrVKHQ6joxUpDhYmTYJbblEZtdatta14cUW3Bw++6rcPVM+wF09k+BFr7RWzBY0xjwL5rbWXLbDu/m8HGfaCkuA2/6Lbtlny40bGqPtagscakHCDxOKhjdp/zyJPRHjRxR3cYvMnC0xvAl2e4mo8kTMeMIrYntgrD27K+9OHVI7t7HHPzfPYnpf4xSbfYyB7rCLCkbF6HBmrph2x+XWLyZf8OHeCnoN+19Gtyd3o9q+WeD+wRlHdlHOJ94j9QrXkk85bVhaK7XOSvdQ750rgmwh5iUu1lk2iUE1XDi3IcJ5hh8MfPPWUbsFK9+7Qqxc8/bSaiHz0kb9HlDEaNFA1jxkzJIa3btUtmKweWYSnNvzN1tqPjDHZgJbA534eluNaY7Kp7XCRunDD/ymqu3W6hPHW6fDrW57ua0aRYG9ZsXIdoOHLEs1Ht6tj2/41yaJy4xgl8aUkIkqR2dzFZJ2ILeARqwVkw4jJ50may+GJCufQ44ioVAZu1X3u3AmJ5nMnk8XzqYMS2HuXwan9skmc2JNskbg0Mp2joKLaZdp5RHx52ThyF5N/ee8yeaTnvqPKGXuW6CLCREjw1nhE9YBLNNMFgyPkcZFhh8ORzOnTaoO9erXKqS1bFlxJgCBBfOGC7BGffaYEwOXLr4lnONgiw8aYwsBga21TT8WJD4DawGlg7JWiwuD+b4ccZ44p8rltluwSO35VcwuQGMxfQfaK+Op6nLecJ2kuu6pLHN6kCOzRrbJKeB97I8InD3DZGsFXS0zeZF9y7mKySHgj1XmKS4TH5pNP+dCm5GoY+1fJKrFvRXIbaW8VjYRGSiws2sB5f0MMFxl2OBwZJzpaXQxHjIDbbw8+IQxw113w3HNKyBw6VK3WK1Xy96h8grV2KjA1xfNdQFPP49N4kuIcYUxULrUZLtFcz+0FVYXYvQh2L5ZgTJqqihVeTIQEcb5yEFcm2acbX0P3OYskV1C4cF72iJP7JYy9kd6zJ5Ifnz+N/MKXEBHliR7HJkeRs+dIFsAxedWww/t7TuxN9i8fXA9Jk5MfH1yX7AsGRa4LVod6bdRQpHAt1WV2pc8cODHscDgupXDh4CmnlhqdO6s1docOimy/9Zb7wnM40sJkk9CNK6XEMC8nDySXKDuw1mOXWCuhnLKhhd5EiXYpPb3ex9lzJft/I2MlxiML6mdSeoatBS6ocsTx3SmIHozDAAAI4UlEQVR8xscVzT6572JPcmoR6Kg8cF0J+ZpLt1VkO39FWSVi4rLwQ3QEO04MOxyO0CIxEV59FV54QaXWrrLRhsMRlsTmg4QGuqXEWtUPPpKipNnRrfLwekufHUlSlPnUfkWCM42nhXP2XB5rRAEoWC25dFvOQp7ybsUlgp2/15FJnBh2OByhx/PPK0JcuLCsHw6H49pgjERnweugYJUr728vqPTbRSXTTvF7BQlvaTVvN7rs3nJsOdXMwq3qOHyAE8MOhyM0KVHC3yNwOBy/C9xYf4/E4UgTVzDP4XA4HA6HwxG2ODHscDgcDofD4QhbnBh2OBwOh8PhcIQtTgw7HA6Hw+FwOMIWJ4YdDofD4XA4HGGLE8MOh8PhcDgcjrDFiWGHw+FwOBwOR9jixLDD4XA4HA6HI2xxYtjhcDgcDofDEbY4MexwOBwOh8PhCFuMtdZ3v8yYvcCWTPxoAWDfNR5OIBHK83NzC15CeX6ZnVsJa23Baz2YQOYq/m9fDaF87l0ON+/wIRznDL6fd7r+Z/tUDGcWY8x8a20df48jqwjl+bm5BS+hPL9QnlsoEK7Hx807fAjHOUPgztvZJBwOh8PhcDgcYYsTww6Hw+FwOByOsCVYxHBffw8giwnl+bm5BS+hPL9QnlsoEK7Hx807fAjHOUOAzjsoPMMOh8PhcDgcDkdWECyRYYfD4XA4HA6H45oT8GLYGHOPMWauMWaBMeZdf4/najDGdDTGDDXGJKXYVtwYM84YM9sYM9UYU8KfY7waPMdqjjFmhmeeOYwx1Y0x04wxvxpjfjLG5PX3ODODMeY5zzFaaIz50hgTFUrHzosx5iVjzFTP41A5dl975jDVc2sXiscuFDHGvOE5RvOMMS/5ezxZjTEm2hjzhDFmujHmO3+PJ6sJpe/39JKaDggHUtMH/h5TSgJaDHu+oPoALYA6QKIx5i7/juqq2As8CkSl2NYP+Mha2xD4N/ChPwZ2tRhj8gHPAc2ttTeiuqQPAYOBJ6y1DYCxwGv+G2XmMMYUAK4DGllrawE5gPaEyLHzYoypA5T0PDaEwLHzUAxoZq1t6rmNIsSOXShijLkNKOw5Rg2A24wx1fw8rKzmHLAaeBMwfh5LlhKC3+/pJTUdENKkoQ96+XdUFxPQYhhoDQyz1h62Mjd/Btzh5zFlGmvtNGvt78WmPVdGFay1P3leHwNUMcYE3R+JtfYA0Nhae9KzKRI4BRy01i7xbPsCuM0f47sarLX7rLV/t9ZaY0wuJIxXEiLHDsAYEwu8Dzzv2VSOEDh2HuKATzzRtg9D6e8ulLHWjkaiwUs29D8lZLHWnrfWTgBOXnHn4Cekvt/Ty6U6IBxIQx8E1Dke6GI4P7ArxfOdQLyfxpIVxKGrxJTsQfMOOqy1p4wxMcaY/wKxwHJSHD9r7Rn0RxCUGGO+ATYBk4BDhNCxA94G3rfW7vE8v+hvL8iP3XzgJWvtTeiYfURoHbugxhjTPIWFJeWtsLX2tDEmARgF9LXWrvX3eK8Fl5uzv8fmQ0L9+92RglT0wZf+HlNKAv3LbTeeZVsPhT3bQoV9/PELuCBB2qLRGJMIfA78z1o71hhTmhT/3Iwx0cAZf43varHWdvFEFQcCRwiRY2eMaQXktdb+kGLzbkLk2Flre6d4+j0SwyFx7EIBa+1kYHJqrxljmgLPAs9Ya9f4clxZyeXmHEaE+ve7IwWX6gN/j+dSAj0yPAa40xiT2/O8JzDSj+O5pniibcuMMa0BjDG3ACustWf9O7KMY4yJAfoDvb0nurV2A5DLGFPFs1tX5D0NKowxNYwx3QGstSeAtcg3HBLHDmgLFDTGjDDGjACqAK8QGscu1hjTJ4UFog2KFIfKsQtZjDEVgGeADqEkhB2/E9Lf745kUtMHgUbA1xk2xnRBkYEzwAxr7bN+HtJVY4zZZa0t7HlcAp0kUcBp4AFr7RY/Di9TGGPaIs/XuhSbJ6PlzU+AC8B+oLu19qDvR5h5UvhpayOf0zbgQRRN7E+QH7tLMcZMtdY2NcbUIMiPHYAx5kngAeAwsB14GMhHCB67UMIY8w66eElpaXnPkwAZ0ngi4o9Yazv5eyxZSSh+v6eXlDog1ElLH1hrAyYpO+DFsMPhcDgcDofDkVUEuk3C4XA4HA6Hw+HIMpwYdjgcDofD4XCELU4MOxwOh8PhcDjCFieGHQ6Hw+FwOBxhixPDDofD4XA4HI6wxYlhh8PhcDgcDkfY4sSww+FwOBwOhyNscWLYERIYYxKNMff6exwOh8PhcDiCCyeGHaHCzUAtfw/C4XA4HFfG0yp9mjEmwvP894CGMSbKGDPdGBPp31E6wgUnhh1BjzGmMfAe0NEYs9gYU9LfY3I4HA7HZekJDLfWnvc8/z2gYa09A0wC3Gqfwyc4MewIeqy1M4F5QHtrbQ1r7SZ/j8nhcDgcYIyZYoxp4Xn8ujHmf56XugAjPdtTC2iM8OzjcGQ5xlrr7zE4HFeNMWYTUM5ae9bfY3E4HA6HMMbcBLwGfA7cB7QDIoAka23hFPuNA5611i73PI8AdllrC/p+1I5ww0WGHUGPMSY/cNgJYYfD4QgsrLXTAQM8A3Ty2CIKAIcu2bU8sCbFz50HzhhjcvtqrI7wxYlhRyhQEtjh70E4HA6H42KMMVWBIsBpa+1Rz+aTQEyKfdIKaEQDp3wyUEdY48SwIxRYDRQwxiw3xjT092AcDofDAcaYIsA3QHvguDGmFYC19iAQYYzxCuI/BDQ8AnmvW/Fz+AInhh1Bj7X2mLW2nrW2irV2tr/H43A4HOGOMSYHMBz4i7V2FdAH+EeKXSYAjT2PUwtoNAPG+Gi4jjDHJdA5HA6Hw+HwKcaYmsAz1tquabw+HHjBWrsmtdcdjmuJiww7HA6Hw+HwKdbaRcAUb9ONlBhjooARTgg7fIWLDDscDofD4XA4whYXGXY4HA6Hw+FwhC1ODDscDofD4XA4whYnhh0Oh8PhcDgcYYsTww6Hw+FwOByOsMWJYYfD4XA4HA5H2OLEsMPhcDgcDocjbPl/zTOUgD6ieRQAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"%matplotlib inline\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"\n",
"def harmonic_eq(x,t):\n",
" k = 0.5\n",
" return x[1], - k*x[0]\n",
"\n",
"def euler_2var(x,func,t,dt):\n",
" y = func(x,t)\n",
" return x[0] + dt*y[0], x[1]+ dt*y[1]\n",
"\n",
"def calc_plot2var(method, equation, dt, n_steps):\n",
" t = np.arange(0, n_steps*dt, dt) # 0からdt刻みにn_step個の1次元配列を作成\n",
" x = np.zeros((n_steps,2)) # n_step行2列の配列を作成し、初期値を0にする\n",
" x[0][0] = 2.0 # initial position\n",
" for i in range(n_steps-1): # 1刻みにrangeは引数個の配列をつくる [0,1,2,3, ...]\n",
" x[i+1] = method(x[i],harmonic_eq, t[i], dt)\n",
" \n",
" fig = plt.figure(figsize=(12,5))\n",
" axes = fig.add_subplot(1,2,1)\n",
" axes.plot(t, x[:,0], 'r', label=\"$x(t)$\")\n",
" axes.plot(t, x[:,1], 'b', label=\"$v(t)$\")\n",
" axes.set_xlabel(\"$t$\")\n",
" \n",
" plt.legend(loc='upper left')\n",
" \n",
" #plot a trajectory\n",
" axes = fig.add_subplot(1,2,2)\n",
" axes.plot(x[:,0], x[:,1],'#ff8800')\n",
" axes.set_xlabel(\"$x(t)$\")\n",
" axes.set_ylabel(\"$y(t)$\")\n",
" plt.show()\n",
"\n",
"if __name__ == \"__main__\" :\n",
" dt = 0.01\n",
" n_steps = 5000\n",
" calc_plot2var(euler_2var, harmonic_eq, dt, n_steps)\n",
" \n",
"\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"You can easily find the solution is given by a trigonometric function. On the contrary, The above result shows non-periodic motion where the amplitude monotonically grows. This is an example showing the numerical error accumulating as time proceeds. In some cases, the error changes its sign step by step, and as a result, the sum of error cause little problem.\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Modified Euler Method\n",
"To motivate the need for improved methods, we discuss why the simple Euler algorithm is insufficient for certain kinds of equation.\n",
"\n",
"The below figure shows the exact solution of an differential equation and the Euler approximation:\n",
"$$\n",
" x(t) = x(t_0) + \\int_{t_0}^t f(x(\\tau ))d\\tau\n",
"$$\n",
"\n",
"This means that the Euler method always overestimates the change (increment) when the exact solution is convex upward.When the difference of Euler method as shown the following schematic figure always has the same sign, the numerical error accumulates as time proceeds.\n",
"\n",
"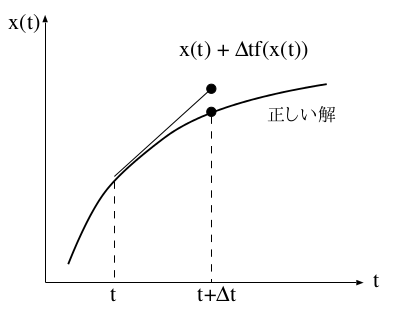\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Euler-Richardson method (2nd order Runge-Kutta method)\n",
"\n",
"An improved method is given by\n",
"\n",
"$$\n",
" x(t+h ) = x(t) + h f(x(t) + hf(x(t))/2)\n",
"$$\n",
"\n",
"which means that one calculate the half-step difference (a trial value) and then using that value, one obtain the difference. This is called the Euler-Richardson method.\n",
"\n",
"Another method is defined as\n",
"\n",
"$$\n",
" x(t+h ) = x(t) + \\frac{h }{2} \\left[ f(x(t)) +\n",
"\t\t\t\t\t f(x^p(t+h ))\\right]\n",
"$$\n",
"where \n",
"$$\n",
" x^p(t+h ) = x(t) + h f(x(t))\n",
"$$\n",
"is the predictive value at\n",
"$\n",
"t + h\n",
"$\n",
"This is called the Heun method (or the improved Euler method).\n",
"\n",
"You can prove that the both method is mathematically equvalent by Taylor expansion of the equation in terms of \n",
"$\n",
"h.\n",
"$\n",
"The following figure shows a schematic presentation for the latter method.\n",
"\n",
"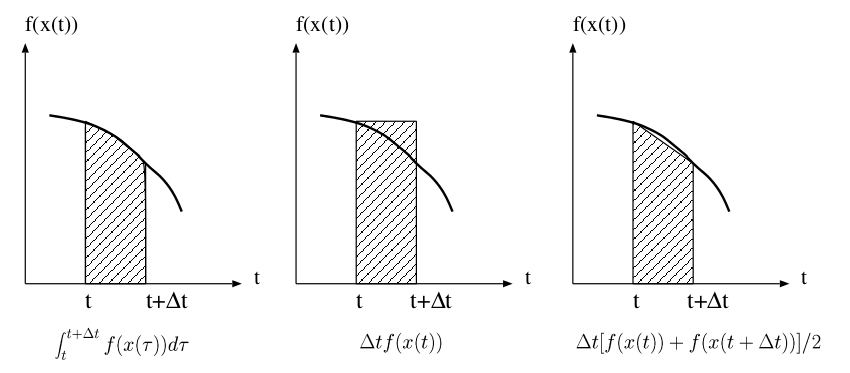\n",
"\n",
"The below is an example where the Heun method is explicitly defined. As shown in the figure, the solution looks like a periodic motion as expected.\n"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAswAAAFCCAYAAADlg4svAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzsnXucZEV593/VPff77O4su7C77IIXQCSsrJoAIigiokZEX4PyShLeSMDba5RL8A1qxGhAJEIMKii+Ji94RQIxIjFcBRFYboLAgruwy8Du3HZn59Y909Nd7x/VNV19uuqcU+fU6ds+389nPtMzffo89Zw6M+dXTz31FOOcgyAIgiAIgiAIPalaN4AgCIIgCIIg6hkSzARBEARBEAThAwlmgiAIgiAIgvCBBDNBEARBEARB+ECCmSAIgiAIgiB8IMFMEARBEARBED6QYCYIgiAIgiAIH0gwEwRBEARBEIQPJJgJgiAIgiAIwoeWWjfAy4oVK/j69etr3QyCIIhIPPzww+Oc86Fat6Oa0P9tgiAalbD/s+tOMK9fvx6bN2+udTMIgiAiwRjbXus2VBv6v00QRKMS9n82pWQQBEHsIzDG3s8Y+zFjbIfh/e8zxn7LGLur+PWn1W4jQRBEPVJ3EWaCIAgiMcYAfBTAk4b31wI4gXOeqV6TCIIg6h+KMBMEQewjcM7v5pyP+xwyAOCbjLF7GGPfYIx1VattBEEQ9UxDRJhzuRyGh4eRzWZr3RSndHR0YM2aNWhtba11UwiCIABgM4BLOOcvMsY+D+BiABfpDmSMnQ3gbABYt25d9VpIEARRAxpCMA8PD6O3txfr168HY6zWzXEC5xwTExMYHh7Ghg0bat0cgiAIcM7PVn78CYB/9jn2GgDXAMCmTZt4wk0jCIKoKQ2RkpHNZrF8+fKmEcsAwBjD8uXLmy5qThBEY8IY62SMXcIYayv+6h0AHqllmwiCIOqFhhDMAJpKLEua0SeCIBoLxtgPGWNHFhf6jQN4kDF2N4CjAHyxtq0jCIKoDxoiJYMgCIJwB+d8lfL6dOX1lQCurEmjCIIg6pjYEWbG2AcYY/czxn5drO/Z5Xn/k4yxhxhjjzHGzotrjyAIgiAIgiCqSawIM2NsGYALALyJc55hjH0VwF8BuKr4/jEAPgjgmOJH7mCM3cU5d7sl1NwcMD8PDA46PW0ZU1NAZyeQVEWLyUngvvuAU04BkkrVeOghoLcXOOSQZM6/sADceivw9rcDHR3J2Ni6FRgdBf7kT5I5PwDcdhtw1FHAihXJnH98HHj4YXGdkuL++4H99gMOOiiZ82ezwC9/CbzrXUBLQhNVTz0l/q43bkzm/JwD//mfwLHHAgMDydggCKKSQh7Y/HXgTocxtFVHAX/6I2DwYHfnJAiFWE86zvluxtixnHO5cq0FgFrw/l0Avsc5XwAAxth1AN4DUbpoidjliXbtAnbvBl7zGiFqXTMzAzz7LNDToxWbmUwGJ598Mu644w6k02kMDw/jvvvuw5/92Z9hYWEBJ554Iu644w60+AmLj34U+MEPgJ/8BHj/+937MD4OvOENQhiMjiYj/K+8ErjgAuDii4EvJpD6yDnw5jcDL70E7NgBrF3r3sZttwEnnwy8853Az3/u/vwA8OEPC7H5X/8FvO1t7s//wgvA0UcDq1eLa5XEAOyLXwS+8hXg8suBz3zG/fkXFoSQ3bNH3LvLl7u38ZOfAH/2Z8AZZwD/7/+5Pz9B7GtwDvzybOB336m+7V0PA9e8Ityx5+4A+hJ4fhBNTeyUDM55ljHWwRi7EkAngOuUt5cD2KX8vBPASs05ruGcb+KcbxoaGrJvxJo14vvUlP1nwzA5Kb7PzAD5fMXb1113HU477TSk02kAwO23345HHhGLy9va2vDWt74VP/rRj8znLxSAW24Rr3/xC6dNX+LWW8X3yUng8ceTsXHTTeJ7Uj787ndCAALAr36VjA3pw623AouL7s+fzQpRDojoZhLIvt65E3juuWRsyLYn5cMjjwixDAC3356MDdnXv/yleNATBBGOqWHgUlb5dVmqNmLZlm+u07f/P/5nrVtG1DGx51IZY2sAXAvgKs75rZ63R1AukFcVfxedT30KeOyxyt/PzgLpdLRUgCOPBL7+dfP7GRE0P+Gcc/DZz30Ob/vTP8Xf/d3fYWpqCldddRWuv/563HDDDQCAe++9F5/+9KcxMDCA2267DTfddBNOPfVUXHTRRTjjjDP053/xRdF+ANjsNltliSeVnXA3bwY2bXJ7fs5LNh5/XIhN11P1v/996fXmzcBZZ7k9P1DyoVAAnnkGOPxwt+d/6qmSOHskoYpd6nkffhh41avcnn9+HnjiCfH60UeFP66j2L/9ben1734HfOADbs8PlPp6YkL8DdLmGwRRyfY7gR++JdpnWQr45DjQkWC6ZBge+RfgVx8PPu6p68WXlwsKyaVKEg1D3BzmDgD/F8Bfcs5f1BxyM4ArGGPfB1AA8OcAkln4x5gQOUmQzQJdXfj7s8/G5y69FKPT03j00Udxyy23YGFhAdu2bcP69esBAMceeyxe//rX4/LLL8fhRbGVz+fx0EMPmc//zDPi+8aNIvUjCQGyZQtw6KHAtm0iD9g1u3YB09PA614nBNuOHe7zZ595RgyKDjssGR84F4L29a8X+d5/+IN7wSzbfdRRyUV/t24Vg8DHHhM+uOaFF8S1kn09MeE+33vbNpFvv//+ok9ck8+L679xoxD9W7eSYCYIAPhaF7CYCT5O8scXAW/+cnLtccHrPia+dGQmgKsC/n9d5pmM/8gWYJnjQARR98QNAZ4I4FAA/6bUFL4DwFsAnM4538wYuwXAAwDyAH4Ye8GfKRL8wgsi3eDII2OdvoJCQUTUVq3Cca97Hfh11+GKK67AXXfdhXQ6jZGREQx4Fgxt2bIFr371q5d+TqfTaGtrw/T0NHp7eyttbNkivp9yinh4j4wAq1ZVHhcHKZgZS0ZsSh/e8Q4horZudS+Yt2wBNmwQfiQRnd29W6QBnHSSEMwvvODehrz2b3878OUvi0GG7p6Ia+NNbxJCNglRvm2b+P72t4t+eO4594J5+3Zg/XohYpPohx07xN+1/JvbuhU44QT3dgii3vnXNwA7fQI6KufNA+m24OMaic7lwIWalKwHLgPuulD/mWtfXf7zJ8fFeYimJu6iv58DOEDz1heVYy4HcHkcO6FobxdpAPm8iEK6IpcT3zs68MT27dg5MoIVq1cvCd/Ozs6y3fomJibQ39+PVs+iuvn5eXSY0kWGh4G2tlLlh+efdy+YX3xRLGZbWBDnd83wsPh+wgnAP/xDcjbWrRNC/Gc/E4OZlMO9d15+WXw/4gixwDMpwbxypRD9gMjJdlm1ZGFB9PXBB4v2y35xiRTMxx8vFv4lYeOFF4RgXr1aDF5cI9t87LHi/0US9ytB1CMzO4F/2T/4uA/eCaw7PvHm1C1vvEB8qVxqmPlVI9SDrwDOTmj2kKgpzbNxiRSoi4uJCOadExM447Ofxc1XX41PXnEFbrvtNrz97W/H4OAg8vk8stksOjo68Pzzz2P//cv/GU1MTGBoaKhCRC+xa5cQyKtXl352ycyMyJFevVq8TiI6K9v8R39U/rNLRkaAN75R+LG4KCKoURaJmpBtXr1aCPMdO9ydW7JzJ3DAAaW+3rnTrWAeGRHpEmvWCBtq7rorhodFfrqczdm5072N7duB444T/Ts6KqLB7e3uzi/7+oADxABmJN7SCoKoax7/DvDLj/gf85ePAyuPqE57GhVvJFonoPf8ofz3lP/cNDTM1tiBSDEqI8KuyOUwl83itDPPxNcuugiHrluHiy++GF/4wheWDjnppJNw7733AgAOOeQQjI+P4/DDD8dvfvMbAMCdd96JU045xWxDpmDst1/pZ5fI8+23n/gaHXWf771rlyjpt3y5qIedhADZtavkA+DehhR+q1eXrpNrxsaECExqcCTbvHKluKeSELOjo8KHFSuEcHbtw9wcsHevyF8+oDiB5doP2Wb5d5fEAI8gaslj15SqP+jE8trjhACUXySW7VGv3ycn9Mdclir1A9HQNF+EOQHB3NXRgft//WsxZb93L4477jjcf//9S4d8/OMfxxVXXIETTzwRPT09ePDBB8tOccMNN+ArX/mK2cauXWL6eWWxoIhrIaiKg+lpkbaSRHR21Soxkl61yr0PMkruHVi4XJQnRdmqVaIvkojEj46KqhVqhNn1+YGSKN+7V1R5cVmffGxMXJ9UKhlRPlF88AwNCdEMiL+94sJaJ+zaJWaili8X9xNFmIlmYM8fgGteaX7/zIeA1Y4rJBGCzmXlEWidQFZ/p8ubJuoaEsxByFq8LS3CRi5XUcVi48aNOOGEE5DP55dqMUsWFhZw6qmnli0CrGDXLuCP/1icf/nyZCPMslb1rl3JCGZpJ0nRL+0kEWHu6RFfQ0NCGLpmdFSIzYEBUQLRtdiUbV65sjyKvWGDWxvy3lm9OjkfVqwoLSacMERvoiJnK6ToT6ISB0FUC7/o5TnPA/3rq9YUokhY8XzavwOvfE912kTEonkEs6z5m0CEGS0t4sGq5kl78pHPMtQEbmtrw5lnnmk+P+dCIKhi0/X0sDfCLH/32te6szEyAryiuMvSfvuJ+r8u8U6hS5uubch+WLlSVF1ZWBALMl0wOyvSDVauFAOuoSGxi51L1AiznLEYHXUrmEdHSxVQhobc94O8JitWlHb4c32d1Eo0coCXRDlHgkiK318P/Nyw0cb7fwEc/I7qtocw4yeef3aq/jii7mgewcyYmGLV7MQXCymYgdJ3jWCOTKEgHtRS3Kxc6T6yOTIirs+KFaVdC5MQIEcfLV4n5YM898CAuP6uc4x37y5FNGUEdXy8lBYQF3lN5LmXLRM2XTI2JgR+X584P1DaMc+lDdWHp592e36dYHYdYR4ZKf+bW1gQsy/9/W7tEIRrTNHkVAtwvuOAEeEeKYpnR4Fv7Ff+nuxbqvNclzSPYAaEoHW9nXE+rxfMrpCL7wYHS9+ffdbd+QEhkvv7RftlzWiXIopzYUMKtMFBkTvrssSfbO/y5UL8Dwy4F4J79pQEsxqddSWY1QV5gLhOrgWzXJDHWOmecmkjmxWzFNKHZcvc94MqmPv6xH3rWjBPTgKvLOZ6yusk/04Iot7gBeAyw//ST88CrV3VbQ8Rn+6VJfF85XIgq/yflnWeD/kA8J4fVb9thJbmEsxJRJjz+VI0WYo/lzakYJZCdnCwFAV2xZ495eeXv3NFJiMi8V4bU1Ol13GR10S1kYRgliJKRjZdik1dhFlu+OIKKZjl+QG310nnw+Sk28HR+HhJ8DMmbCQhmHV/Ewce6NYOQcRh+mXgat1WB6Dp+2bifxf/v+19AfiWkj73zI/FF0D9XQc0l2BOIsK8uFiqMCAFQRIR5iSFoCoO2tuFPy5tSDGrRskBYcOlYE6lxII8acP1wEK9TvK7Sxte0Z9ESoY30g+4tSHP5bUxOVkaZMRlfFycX/69LV/uVjBzXn5vJjHrQhBx2LkZ+NfXV/7+pG8CG8+pfnuI6tC/viSMvak38mcSzjWjuQRzOi1yEV2iRs5kSkYSEWb14T0353axmSoEpS2X4kCeyys2XYvygYHSoqyBAbdCUKaVeEWUS8G8d6/4Lqf9pWB2udhs797SosjWVrHttsvrpPMBEDZcCmb1XCtWuBXMs7PibzjJWReCiMLOh8RW1V7O3QH0ra1+e4jaQcK57mguwew6wsx5uWCuVkoGIB7e++2n/4wtk5Niq2SJa8GsS5cAkhHMksFBsc20K2ZmRL/KtktBKAWiC3Ric35epLR0OcpB3Lu3PA/XdV/7CWZXqAMXQLx2uXV1Ne5XgrBhahj4pkYQfyYDtHRUvz1E/UDCuW5oLsEsc5hdReykMJZCWVbiSDolA3AvmJOMMNdKMLuM/nqj5H19or9dR5jb2kT9ZaA8xzgpwew67cMkmF329dSUuP6S/v5S/XAXmO5X1yk+BBGEaTHfeQtA2lElJqI5kML4shaAK0G7S5moqPERx+thiAqaZ2tsQESYOXe37bMUzC3KuMKzsDCTyeDNb34z8sXfDQ8P40c/EqtaFxYWcNxxx2HRT2AXCuUiKomHd60EczV84I5G1/J6yLanUkK0uRbM/f2lwZzrHON8XlSwqKZgTiJP2lvera8vWcHc2yv+rinCTFSTS1mlWP7UlBBGJJYJExcsVkaVdz8r7qdnb6pNm/YRmkswu06Z8EaYgYq0j+uuuw6nnXba0g5/t99+Ox4pbqnc1taGt771rUsCWkuhUJ6b6zo6u7goRJQqNl2XZKtGhFmt9CFt5fMilcIFXh/ka9cpGaoQlK9diUG5KY3XRpJpJa59kOfSRZhdDY68i1STKlNIEDouZZXT63/+sBBB7b21aRPReFzIK4XzTaeJe6vguFoYAaABUzI+9SngsccMby4OAJkOoDttNRQ48kjg61/XvKEI5ocffhjnnXce7vzWt4B8Hk8++SQ+8pGPgDGGG264AQBw77334tOf/jQGBgZw22234aabbsKpp56Kiy66CGeccYbeeKFQma8JuHt4SyFTzQhzV5dYcJZ0SgYgbPQ6eMh4I8yAsOc6Sq6KWdluV2LTK2alDSmkXdlQZ0Rc+yDPpQrmvj7xt+gq11s3OEqiOg1BqLz8IPBvbyz/3WvPAk75bm3aQzQHuhznr7aUv0c4obkizCjeMK7uERlJbmnBoYceimeffXYpJeNzn/sc/v7v/x7btm3D+vXrAQDHHnssXv/61+Pmm2/GY489hg0bNuDwww/HQw89ZLYhI8wSKRRcCRBvNE3amJlxG7Hr6ipV9WAsmWl0r5gF3EVPdSKqvz+ZlAyJ7GtXglYnmPv63Apmb7pEV5dIX3Flo1AQ5/IKZsBdX3vz1aUNl/crQahcyirF8oWcxDLhjgt5ZR7zpQx48IratKcJabgIszYSLJnJAs9sEZtPuNixS4kwd7W3o6OjA5MzM9i2ZQv27NmDww8/HAPqQxfAli1b8OpXv3rp53Q6jba2NkxPT6NXFwn1CmZ5jCsBohOCvb1CLM/Oluoax8GbLiFtuPJhYUGU2lNtyHa7SsnQiaiBAWD7djfnB8pLvgHVizDLdAYXC2G9op+xkg0XyP7UCeapKWD16vg25N9EkpF4ggCAH54IbL+9/HcXFNyVkSQIlWWvEsL56rXA9LD43Z2fEV8UbY5Nc0WYU0V3XC/6K+YnH3bYYXjm+edx8Te+gS996Uvo7OxENptdOnxiYgL9/f1obS1fsDE/P4+ODkNpoEKh/MHd3S3+mboWzLpUAJc2vAMUlwLEJAQBdzbkeVSh5jolwys2XftgijAvLoryda5sqNcIcNvXUnh7c5jV9+IiZ0TUv1MSzIRLOBfRPVUsv+UKIVpILBNJ89EXKwXypQz43pG1aU+T0FyCOalFf0Uh/prXvAbfu/FG8EIBxxxzDAYHB5HP55dE8/PPP4/999+/7BQTExMYGhqqENFLcF4uDhgT0dMkBYhroTYzUx0RlaTYnJkReblqRZTeXncRbMAsmJOOMLu24R0cuUxn0N2vrlMykr5fiX2bbx8MXOZ5tF7Igdf/TW3aQ+y7XMiB9/+i9PPo45ULTonQNJdglhFmV4K5UJw6UwTztTfcgEvOOWcpin3SSSfh3nvvBQAccsghGB8fx+GHH47f/OY3AIA777wTp5xyir8Nb1qEy4f37Kz4rtqQIsqVGJyZSdYH2U6dDy5teH1wOXDRlXxLp0Wks5Ei8TrBnHSE2XVef9L3K7HvcikDJreVfj7rdzQVTtSWg9+hjzbffHpt2tPANJdglhFmlykZSkm5D3/4wyjs3ImjDj10ycbHP/5xfP/73wcA9PT04MEHH8STTz6Jo48+GgBwww034Oyzz9afn3PxpXt4uxSzonGl38nXjSI2pejv7i79rhqCubdX5E+72G5dV/INcLsoz5SSodp3YaPaEWbXKRlJ36/EvsdvL62M3F3IgaHX1qY9BOHlQg58+IHSz8/8iKLNljSXYE6lRETYZYQ55blEnij2xo0bccIJJyxtXKKysLCAU089tWwRYMX5gWQf3rWKziYdYa6W6AdKgj0OOiEIuF0wNzUl8nLVfPlqpGS49gGoTYR5bs7ttvfEvsGlDLj7b0s/n347RZWJ+mT/N+ijzeNP1aY9DUYswcwYez9j7MeMsR2G97/PGPstY+yu4tefxrEXCs9OfLHwRJiXzg+URbHPOuuspY1LVNra2nDmmWeaz28SzEmITbV+bTMI5vZ2kW+cZFqJy0ocutQYwG2EWfqgLipyGWHmXH+dXPpQrRxm3f0KuBkcEfsGhUV9VPnAt9SmPQQRlgs5cMwXSj9/9zUUbQ5B3AjzGICPAmgzvL8WwAmc8+OLX7fEtBdMKuUuJUMXYXa5sLBagrmrq1z4V0swu6r1rBPMspxZNSLMLgWzmlYCuI3Ozs7qzw+4sTE/b865dx1hVqPYra1igJT0/QpQWgYRjl99AviqspB72SEUVSYai2M/r482E0ZiCWbO+d2c83GfQwYAfJMxdg9j7BuMscjbdPGwwstlhNkvJcOBKOeLi8kv+ktaHBQK+nrOvb2iH5Sye5HRCWZpoxqC2YUN6YNX0LqMzvoJZhc2TKJf+uBicCQFs7dmeXe3u+gvCWYiDpcy4JFvlH7+1BTwkadr1x6CiINONGd216YtdU7SOcybAVzMOT8OIhp9se4gxtjZjLHNjLHNY2NjFe93dHRgYmIinGhOpaqTkhHTBuccE7t3o+MPf0h+0V+SQnBurvycEpcCpBqCeXq6UqQ1YoRZly4BJCv6e3vFwEneC3GYmqqcEQGEXySYiVqjS8Fo12xIRRCNxIUcOOnq0s9XLQdu/Ujt2lOnJLrTH+dcLQ/xEwD/bDjuGgDXAMCmTZsqVPGaNWswPDwMnZiuYGREPLxdpGXs3CmmgnO50u8WF4HxcX11C0s6pqex5gtfAP7jP8rfcL3oz9tOl+XM/MQsIGysXBnfBmNAZ2f575O+TtXKYXa5mM0rZuXPLmz4RZilDe97UWzozpF0hNn1IlKiuZifBr7uWbBLKRhEM7HxXODIvwYuKwYrfvcd8UX3+RKJCWbGWCeAzwK4hHO+AOAdAB6Jcq7W1lZs2LAh3MEXXww89ZT4isvxxwPvfS/wrW+Vfjc2BhxxBPDP/wx8/OPxzv+zn4ktmf1W7GsWE1qhEwfShgshaBLMrtMZursr02MaKYfZFJ11KQRnZ4GhofLfpVLCjyRFv/TJhR9zc2bB7MIHWSaQIsxEWB7/LvDLvyr9/N6bgFedWrv2EERSsJQQyOpMyqWMRHMR5ykZjLEfMsaO5JxnAIwDeJAxdjeAowB80bW9CpKoOqCSRF6r6eHtSqiZBHO1IswubCQp+hcXRa51kv1gis52dwOZjJsZEV1KBiBmE1yIWT8fADcpGUlHmE2ifx8RzCEqG32AMfYgY+xhxtjXqt2+uuOKnnKxfP4iiWWi+aHFgFqcCGbO+Srl9emc88eKr6/knB/JOX8z5/xDnPPkn0Yxp+l37ixqF5mT6X2wdnSIqG9EG9ks8NJLxR8SEptjY8peGyaxGeM65fPACy8o55fnU4npw/g4MDmp2EhA9D//fHGdmklExYwwz84Cu3YpP+hsSHGYyUSyMTIi9P6SDZPYjChmFxeB7duLP/hFyaX9COzerbg/O1teAlESI4eZc2DbtmJfV2OAV98YKxsxxg4EcAmAtwHYBGANY+x91W1eHXEpA3LKPXchB1IxZ/wIolG4kAOHfaj086UMyOfMx+8DNNfGJUAscfDTnwL77w+cfz7Mi9lkObOIIupd7wI2bChmjCQQYX7iCWDNGmEHgDnqGGOa/rzzhA833YREfNi7Fzj0UGDjxmKRDZMPMQTzddcBBx0EfOlLMPsghWAEG5wDJ5wgbGzfjlIetrqpiGojghi8/37ggAOA0+UOp7ocZmkjotj8678G1q8Hbr8d5gizFLgRbOzaJa7RUUcVhb9fSkZEH668Ejj4YOCqqxCcQuRqsW2dElDZ6GQAN3LO93KxwvrbAPbNcKpucR9B7Gu8+/ry3QEvbwN2P1e79tSY5hPMXV1ikV7OfiT0zW+K79/9LpDfa4imSRsRRPmWLUJ45HLA978P82I2KUAi2Pjud0V0+Ve/AnbsgL+IinD+XA749rfF62uvhTlyGsOHn/5URJhfeAH47/+G2YeI/QAAVxcXBF97LcCnDSIqnRZ9E0FEbd4MPPSQiJxefz1K0V/meRDHEJvXXiui/TfeCExMwBxhjpiSMTMjBhYA8J3vIDglI4KNH/xADJCefloMAHyj5BHFrNrXRsEc435tIpYD2KX8vBOAccVuUHWjhoXEMkGU2P8NwGeUGdBrXwVsubF27akhzSeYI+ZTLi4CDzwALF8uHuBPPFzMaTDlhEZ4sN5/v/g+OAjccw9K4sC7mC2GAPnNb4QPAHD33TCnM0T04YknhAgcHATuvRcoTLkXIPffL07X1la8TiYfurtFCNqyxN/cHPDYY8KHF18EXni22NfesnJA5Ej8ffeJ78uWKX1t8kE2KoIN2df33pMXG4uYbEQ4/0MPie+Dg8V7KSitJKIPAwPi9ZINXUpGxAjz+Djw3HPCxu9/D4y/NC/e0A2O2tv3dcE8gnKBvKr4Oy2c82s455s455uGvItNGxUSywRRSUtH+d/Cv78fuPcLtWpNzWg+wRxRqD3zjHgen3OO+PnJJ4o3h0mARHh4P/igWJP4oQ8BTz5ZjGyaxCxg7UMuBzz6KPAXfyHE5pO/Kwh169gHADj3XJGpsH1H8QHjsHLCww8DRx8t0jKeeAL+oh+wzv999FGhsc89V/z8xBPFNxymrmzeLFJj3v3u4vn9IqeA9XWamgKefRY4u1i48clHcuXnU4kYYZZ9fc45Ird/YjSvtxGjrzdvBk4+WaT4PPkkzNcpYg6zFP0f/aj4/vunU6XzeXFZsaQx+QWA9zLG5MjxLAA317A91UUVy6/+HySWCcKL+jdx398DPz+zdm2pAc0rmC0ffH/4g/j+zneKnXifeKq4uMNhdPa554BvcFZpAAAgAElEQVRDDgEOO0xosJfG2pwK5h07RKT8Na8Rdp54vChwHPvQ2SlEDgA8/UKn3oZMM7G0USiI6fkjjgBe+9qiiAoSzJY2niumYL2vuJzpqWeL1RUdCmbZ14ccArz8MjC1J28Ws4D1/bp1q/h+1FEix/jJJ4pVNhzm/z73HLDffsAxx4ifn9nRpc/DjujD/Ly4Z1/9auDww4t9PTdnjjDncspq1vA+AMBpp4nvT/+huJ2xw7+JRkepbLQTwJcB3MMYewDACOd835h7VcXycf8AnPrj2rWFIOoZVTT//t+An767dm2pMs0nmCNOD0sBcsghYoHQ1u0+Iirig3XbNrHA6dBDxc/PjAw6naaXPhx8sBAhW7caor9AbB8OO0z8/Mxwj0gpaW8vPzDiFPfIiBBSGzYAr3wlMDwMzE9r6uYCkSOb27aJJh9+OLB6NbBle7HtDquJVPT12PJk+3pbqvx8Xhsu7teX+/R52BF9eOEFsTiydL8CfMZtJH7bNnHZN24Up3hme1Hs7+OC2aey0fWc842c8zdyzs+rXQuriCqWT/ke8CefrV1bCKIRUEXz1p8DP3tv7dpSRZpPMEeMOm7dKnI1BweBdeuAF0eKVZccTd0uLopo2kEHiYggAOzY0+sfOY0gDgAhQNatA3a8lAIH/H0Is924x8aGDSI3t6cH2DHeJV54RZRqwwJZrm79euEDALw4YxhYROzr558H1q4VaSsHHgjsGPERzF1d1ikfU1Mid/bgg5W+3tvvVAiqgnndOmDHywEzIhEizM8/L+7XtWtF9+7Y3a0/f3u7GIHEvF+zWWBsvte5YN6wQTRv/Xpgx6iPYKaUjH0PVSy/+wfAa/+iZk0hiIZCFc3P/TvwXx+rXVuqRPMJ5hgC5KCDxOt164AdY24jUcPDQjQfdJAoXQcAw9P9ToXg1q1Cu6xeXRQg8ymMY4XZRqFgNcUt69kedJAQUGvWAMOTPeYtwiNcJ1UwH3igeL0jt8rpdZI+AEIMDk8Uz+OoEocUswcdJK4RUOxrxykZK1aIdYrr1gEjE63Iot1ZSkYuVxrgtbYCq1YBw5MGMctYJFHuFf0AsAPrzHWYgUiCWfb1mjXA8G63fU00MKpYfuf3gcNONx9LEEQlqmh+9GrgkX+pXVuqQPMJ5ogi6qWXSg/ttWuBXXu7MI82Zw/WHcV9tQ48UIjalSuB4dlBvTiI4cOaNSKaViZA/ISahY3JSZHOK4XsmjXA8HSf/vzSRkTBfOCBJTvbcaAzHwDRF/Lca9cCL072iEi8t7yftGEZYR4eFt/XrROR+I4OYHhumdPIqfd+BYBhrDHbmJ+3qiby0ktiPFXe1wbRL21E8KG1VfwtBN6vEa/T9u0eHyZ7xdRCS0vlwSSY9x1UsfzmrwCH71uLlwjCGapo/tXHgeF7a9eWhGk+wRzxwbprl1jgBJQe3sNY46zEldzxbVUxc3DtWuDF+ZV6kSYf6BFsyPMHRuwiXCedD8Ozg3ofpA1LH158UYjM7u5SdPZFrHXmA+ciT1r1IZNrxW4sq8zDBoRvEfKwAWFjKRI/P+Q0h1l3v7ocHKk+AEUf5gb9BXNEHxizEMwWCzDn5sThqg+7Znuw0Nmv/wClZOwbeKth/PHf1q4tBNEMqKL5+jcBmYnatSVBmk8wRxAHuZzY+EEKkNWrxfcR7FdZEUDaiCiipI01a4AXc/uZxWZEG1IclPlgipwCkUSU6sPO7CAWO9ylZIyOls7f1gYsG8g79WHPHtHfqg8A8FLrhsp62NJGxL5eubJkYzi3Ui8EpV+WQs3Y144WR3r7eu1a4MXskNMIs+rDsmVAa0tB+OBocKTzgSOFl1sP1H+AIszNjyqWWZqqYRCEK1TRfNUK6/VRjUDzCmaLB6vcpEo+vKXQGUntb566XVgo7uUbjpERUThCbjSxahUwkl/hXDBLcbBihfg+ipVm0Q/EEsyrVgEFpDGe3k//gQg+jI2Vrj8ArBzMJeqDtDXatkb/gQg+7NolNsqQTV69imNXwSCYI+T/Fgrlfb3kAww2HIjNVauA6Xw35jqW6T8QIYdZjZIzBqwcXDT7ECGHWecDAIy0uutrooH4J8/GRBeE//9NEEQILiiUXl/WfPKy+TyKMMUtUw0qBEjrAc5sjIwAQ0OlIObQEDDBlyHf5iadwRslb20FlnVnhQDRiXIHIkpu7jWWMgjmCFHH0dFywbzfYM4cYXbpQ8tq/QdkDrPFaFkVswAwNLiIMRhSMgDrdIY9e8RYTQrAgQGgJVWMxDtOyZB9sXSd0qv0H4iQkqFGmAFgZf98oqI/lA+UktGc/O57wIKSzkObkhCEexgDPvZy6WfvzpkNTvMJZhnWi5GvKR+so2kfERXBRpmIWsHBkRK5syYbFucfHRXfywRIT8Z5dFaNki8JEGbYFjdiSkZZhLnfR/Q7jDAbRZS0kc1a2VD7YahvHlPox3ybZuttwFqoeX1IpYChrjlxnRymMwwMlNK6XQ+OCoXy9BsAWNmXce4DoBPM7mZEiAZgYRa49azSzySWCSI5elYDb/9W6ecmEs3NJ5hTKevpYW+Eua0NGGibxWgqQERZCjVVCA4NiK2MxxYHzTZiRMkBYGX3rHOx6Y2SA8AYdyOYczlg9+7SeQFgvz73oh8oXafBQSDN8hhlPiLK0oaaagAAQ71CbI/z5WYbMe5XAFjZOY3R1GoxovESUWyW+VDsk3Gs0H/A0ofdu0WUvPx+nTNHmOU9bFGxxBglx0r9B7q6RKNyudA2iAbgn5SZHRLLBJE8R/51+c+XaxbUNyDNJ5gBa6HmFVEAsLJ9L0aZ4cHqQoD0zQMAxvMGwRwx6lgWYe6cdp6SoRNRY3lDlNzSh/Fx8b0swtw9hz1YhoUWTdSxpUWMbix9SKfFIjNAiP/lrVPmKHmELb4rIszd4rNjC26qM2j7umOvU9FfMcBbIYSGq772vV/9BLOlD2qUvLsb6EjNY4wbRH/ECjtEHaNGt86ngRBBVA11cJpfAIbvq11bHNGcgtny4T06Kj6iPqdXtu7BaMEncgqEfnjLUmZlYrNHRMqMIipiSkaZ2OzYKwSIaeEiECutZPlygKHgLEqu9aFL5B2OzrmpxCGFoFoQw2Vf53LA3r3lUfIlwTzfp/+QZf6v9jq17cUoDD64GBzJGZGcj+iP60PnFObQjVmuGRy1tor72DLCrPrAGDCU3o2xgk+kH6C0jGbBu4tfSvN/kCCI5CgrN3ds7drhiOYUzJYiavfuUsRRsrJlN0ZND1bLRX+ZjEiBXaEEtpYEc9aQ1xrBB6Dcj6G2KUxgBRbzhm2rASsbExPlPqTTwDLsxlhuQP8ByylunYha0T4tbGc0IkraiOEDAAyl95gjp5Yias8e8X1QGUMMdQrRP5bxWfRnmc4AiOipRIh+n3QJwMqG9zr1t2XQghzG5t1EybX3a+teAD6Do85OK8Gs7evUbv8BHkCCuRn47aXlP9MufgRRG1TR3OD5zM0rmC0e3nv2lAscABhke7Enb4gIWgoQnYha0Sk+axTMlgJkzx4RNe1VTjeYEgJk717NByKIqIrrxDmGMIaxBZ/IqYUNWd5Pjc4uaxWCeU/Wp5qIZYUJb18PpSYw6khESSFY1tdF0T/uJ/ot+6G/vzxdeZBNYpZ368cmloMjziuvE8tmsALjGMv6RPpzudCDI93fxCCbFO9lNPnqgLVg1vX1CjbhHyUHKCWj0eEcuFvZjITylgmitpz1u9LrBhbNzSmYHYioQezBnkWf6C8QK+rYtjiHPuz1F1GWPgwMlKcaSMEs7ZfR3i7mqEPaKBTE1thl1ymXwwqMY9wvSg5YXyc16jiYnhLvzRkWDTgYHC3DbuzJBfgQUqjpfFjWMoUU8hibMfS1i/tVik1dX1sKwZkZsYt2mY1sFkMYw3jGZ+MSINbfxJIPk4Z/qJa7LmoHRxjFuGmARxHm5kCt/0pimSBqz9Bry39+/Du1aUdMmlMwRxCbFQKE70a20K6vJmYpQHTiANmsEOWmaJoDH5axPWX2y2DMKoo9NSUCN2U2MhkMYg8m5302XwGsRZSaaiBF/+5ZH8Ect68LE5jMdelLLTsYHKXmM+jHXkxmDD44iJwO8t1l9suQFUYsRb+2r02RfssqFnv2iJRkdd2Arw9AqSZ2SLTXKT+ByQWfQSpAgrmRUaNX575Yu3YQBFGOOnj95Udq144YNKdgjpDOoBNR8r0KHIioJQFiElHd3UIcFAr69z3s3m0pogArsekr+rMG0W85sJicFE1qayv9binqOG1YsONAMA8UdmORt+ibaVmdwa+v98y2aT8TRTB7c+5971fGhGiOI5iXBng+oh8IbUPer0zRN8vyY2X2tTZCnj+fF4O8ir7OT2DvQqf+z4pSMhqbF39d/nOfYUdHgiBqQ4PnMzenYI4goioESPHhLXNSK84PhLYxOVk8p0dEDWASk3MGERUhFaDqgln64BclB6yu04Bn/WBvYS/SWDRP01sMjnI5kW5QcZ0WfYSagxzmpes0axD9LiLMfoLZ0oZvX5vu1wgR5iR90P7N5fMYLIyjwFOYntZ8iCLMjc0Nx5VeUyoGQdQnp99Ren1ZY1WuiSWYGWPvZ4z9mDG2w/D+BxhjDzLGHmaMfS2OLSsshOD8vDi04uGdCyGiYqZkDGASe2Za9R+KEMU2CUGt6AesxKaf6J/Ktuojdg4EM8tmMMgmnYh+6YPXxmButOz9ivMDsdJKlsTmjI9gzuetFsxV3q/CB2NfxxXMxft1ctZwv0ZI+/D60LUwiVaWS3RGZACik130NVFHqNEqEssEUb8ceELpNc8DPNwsej0QN8I8BuCjACrCToyxAwFcAuBtADYBWMMYe19Me+GIKw5QEiDah3cqJRbNWT68+9XF+TIlwy/VALAS5VaRU8CZiOKcYWpK86EIPnjFLDIZDKam/EVUnIFLPo+B/HjZ+xXnB6z6urdXlA1eQgrmKc0ufICV2OTckH7jsK9Ng6NB7MHUbAvyecP5i8eFQXe/svksBlumnYh+rQ9hBTOlZDQWT/5b6fXrPla7dhAEEQ51UHuZ4blYh8QSzJzzuznn44a3TwZwI+d8L+ecA/g2gFPj2AtN3HxNzjE4v7Ps/Qo6O6FfEai34S0DtiSipg1dIAVICBu6MmAA0LEwhY7UfKLT9IPwWVho4QOgjzAjm8Vgi49gtuwHQJ+bK+1rzw9Y5+aWkSlGyf2qP4S0kckACwsawTwv9stOenAEGMoURhDM3jQoZDIYbJ1pmPuVqBP+88zS67d9o3btIAgiPB99qfS6QURzkjnMywHsUn7eCUC71zRj7GzG2GbG2OYxWYw3Dp2dYsOMxcXAQ7UP1vl5/wertBEjmiaF2sxsSj8TbyFAZmeFq1oB0j5XFRHlQmxWlK0rfnawdSa5VIPiwEV9v4xUSgzAYqTGIJPBQMus/hoBVtfJNCPSNj+NrhafwZHlINJb01u9TokNLLJZDLb53K8WVTIi3a+WaSVEHUCpGATRmPTuX3rdIGkZSQrmEZQL5FXF31XAOb+Gc76Jc75paMiwva8NFpGioAerKwGiFVGOInbahWbFz/oKZksfvGXAAkWUpQDRRpgzGQy2zgaLfm1NuHKCIsy+NuIK5tZZzM2J6LD2/MXjwpwfMAyOOrPOBkfemt6B18nCB21N7+JnBzsCBngOFqkChvu1pcV6+22ihux9ofT6Fe+uWTMIgohIg1XNSFIw/wLAexljMk51FoCbE7RXIq4AyWTQgjz6OgLSGSxSAXTRNFdi0xR1RDaLZZ0Zpz6oZcBcTnFzbk7JWNbhI5jldZqfD7RhElH9ECMWYwTYcrGZaeACxB8cmfKwkcs5Fcx+A7y4EWZtTW9AiPIOdz4A5pQM32g/pWQ0Bt/aUHr9vltq1w6CIKLzwTtLr+t8QxPngpkx9kPG2JGc850AvgzgHsbYAwBGOOc3uranJa7YLD4wB7t9Vuw7ECCDrbNlbag4v9KWoPMDBhud7nKYdWLWlYianhaRR12EeaAji8lJQxA5wnXyVrBIo4C+TjfVGUw5zAMdmbI2lBFXMC/drwvJ3q+Ocr397tdlXSEEc8jZhPb2UrMAANks+jAFxriT60TUkCuULdrPD069IwiiTll3fOl1nW9o4kQwc85XKa9P55w/Vnx9Ped8I+f8jZzz81zYCkWEh7dXRAFAf/eiPiIobcQRm4qISkyAZLPo78o588E66tjevnRcEKaSb8hm0d+xgHzecBrL69TRURpPyfMDwEBPzkmE2ZRqMNAxv/R+BXH7uvi5AYf3q9+MSCKiv2ijv1vcr8ZdFzk35LVU2tD1Qwocfd15/wgzCeb6J6dUMkk1xoIhgiAMNEhqRnNuXGIRdZyaEs/hFrW6W/GB2deT15dLA6zyf7UiKpvFQHt26X3t+ZW2+CHbWFa2LpcD8nn0dS/6+2BRwUInQHoxjVSK632w2GFOWwasaKOvU6yK1PphIdRMPgDAYF8+9mKzxUVxWF9fpY2BroWlNlRgmc4AeGwU+7Cv2+d+tSzJph3gtcwuva89f/G4ILT3a/GzfV15FAoBg6MQgxeTDwAw0OsjmC3+JogaQQv9CIKoAc0tmEM8vGdmPNUAgJIA6SnodwSTNkI8WKWIqrCRyWCwS0Qd40bsZmbE9x5llnJJ9Hfn/X0IKaKmpzVCMJtFChz9/fHL7xkjzJkM+rpF4V+tGJQDixA2TD4AQH9vwT86G6I2rzykrB8A0dc9QvT7is0QPsi+9lawAELcrzH7uqdjEem0oa/b2sQAKer9yjkwP4++HrFaOu7gyK+vB/spJaNhKShFwF97Vu3aQRCEWxogykyCeUYvcACgr5fHjthJEaUTzP1dISKnFiKqzI8l0c+xsGBYE2exw5zvdeoz+CBtRE2NAYBsFr1dPoLZUV/39iD24EjbDwAwN4f+HuFD3OjszIyYDWlTtwqSfR10v4aMnJquE+vqNPc1Y6H72v9+9RHMFtvFJ32/EjXiq8pU4CnfrV07CIJwz0lXl17n6u//cHMKZot0Bv8Hq2EHOyCeOACAbBbdXRyMuRGCUq8soYh+ICA6G+c6tbU5uU5SSGqn6f18sIw6Gvu6P76IkoJbZ6O3h5cdU3F+pS1+yH7wVisBhBD0HRyFWDDHuaGvs1mgo8OJ2NReJymYi1HhRAZH0oZfX1ukWhFVRi0j95eP16wZBEEkxMZzS6+v6KpdOww0p2C2iM5qRVTYB2ucqGMxYtdjimxaLJiTPphEFBAvis25z3Xq7ERvr090NqQAkZ/XCma/qKOl6Dem3/Sn/H2Imi5RbFtPr+icuII56H4FfPo6xIK5bFZMOmgHFkF9bTmI1KWVyN/53q8hcpj9Bke9fn1NZeXqF7WM3MojatcOgiCS45znS6/3bK1dOzQ0t2COO03fn0YmY8hYiBt1LIrNvj6DAEmlhGiOKQR7+0UXx4nYLSyIXGydEJQ+xE0F0A4sirs19vULsekidcVPRCXiQ9FGqqsDPT1uIqfafoC4X4F4NvxmRGSE2VXqStkmOFL0D8S/X6UN03XqG0g7yfUmqsjOh0qv/2amdu0gCCJZ+teXXl/zipo1QwcJZr8H66C4PMaoYNRomrTR0YHeXjdi05hq4ECA+AlB6YOLqKPchXqJpchpCMEcN/1mWRrZrGFwFDJK7nud/KKzlgvmjBFmh31tGhwF3q8hfWhvB1pbPedHQF/HzWHOZgHGggdHJJjrj399Q+l1W7f5OIIgGh91UDyxpXbt8ECC2U+ALBMLTLQip6NjKQIadH4g+SnuIMFs9EE51u/8QLIpGdrc3GoIZhmJH/Dp65ADF78cZt/rZLlgziz6A3xQjvU7P2COMCd2v4b5mwuZklEoiMW2xn7oY8hkDH+6lMNcf4w/XXp9XvCOngRBNDjqoPg7h9SuHR6aUzBb5LX6LgRbLkJgcVIBgsSmbzqDRf6vUYA48MFXCIZZCBYzSt7e1462tnhl5YyL2TIZIJVC36BIZzAOLLLZwAVz2uisHFSFSV2pxv0aZzahGj4Mxk8r8SvvJ32Q7dDaoBzm+uK7h5Vep9vMxxEE0Tx8SnkIZE11QKtLcwrmuHmtS9Gu+AIkSGy6itgZ00qKEbvE8lqLkdOZGRHZ09qIGTn1FWohfZibE3rXmGrQ5xPFlqJcW36ihF897ERnE2wGR3HuV4c+mHLu2/s7zIOjkCkZYaLkQLxUK6JKqKWlPmUqlE4QRNPRrjwkrlxWu3YoNKdgTqdFgmSIxWy5nEFEtbcnn//rt+hP2ogr+leIiEySea19fUKMavf2sIg6mkSUbxTb4WI22Y64NsoWs8nPdHU5ic76Do6GRGWVONVEwi760wbbXQyOHPa13/0K+NiYnzeM/poDxtgHGGMPMsYeZox9TfP+XZ6vN+jOUxXU0lLt3p1oCIJoav7XU7VuQRnNKZiBUA/vMGIWSFaA+C6issz/LaP4uc7BDqTTCfmgRMkBn3SGJCPMIcvvhcklB+KlfUxPmxezuc71LkPmYa/wEcwOF/3FHRz5+eC7sDBkDnPs+xUInE1oVBhjBwK4BMDbAGwCsIYx9j7PYe2c8+OVrwer3lAvH7yr1i0gCKLarDi09LoOdv9rXsEcQoCEnbqNm8Pc0SF2Z1tC7q6niKikInas00eUO8rDDrxOMXOYfaOOjIWqkxx2cBQ3wmyK/rqoMFEo+Odhdw+0xt4IpxrpDH45zL597XCRqmxHBRaLSBuUkwHcyDnfyznnAL4N4FT5JmOsBUA/Y+zHjLF7GGOXMMbSNWmp+oBc9+aaNIEgiBpz1Cdq3YIlmlcwhxBqQfmaLnYdCxM5zeUCdmfzQS5mM6YzOMj/DXud4pbf84s6xk1nkG3TXiclJSNOhDlMX8fJ/5WBVZOYZSlmtlFnfR10vxprk4cYCFfj77qBWQ5gl/LzTgArlZ97ANwN4GwAxwNYDeCvdCdijJ3NGNvMGNs8NjaWTGsBoG9dcucmCKK+OfGq0uvL22vXDjS7YI4z/dzRsfTAjStAjEIwTMQuQKRlMiLyGBSxS6TUWJgp7s7OUkQ9wEaklAxpI8mUDEeDo97eEFtXB5wfMKdLAHCS/5tKlQ4HIEZlYWddksxhDmnDeJ3CRMktKuw0KCMoF8irir8DAHDOJznn5xa/FwD8DIA2h5lzfg3nfBPnfNPQ0JDbVt5zcen1udvdnpsgiMYk779TbdKQYIZ56jadhnl3Novp4SAhCETP//UVgq2tQDrtZIqbsVKRgiWU0nhAAtcpzKI/aSNmSkYoERVixiJyX8e9X4ttdCGYK+phLywI0RwmnSHEgrlYswkO+zruzpENyi8AvJcxJocTZwG4Wb7JGFvFGPssY0t3wMkAHqlyG4H7v1R1kwRB1CkXKjmrmYmaNYMEM8wPViCEAAnx8Pabfo4bsQsS/YAbH7q7ReSxjLAR5gAbvjWSi+dILMJcFJstLeI0ccVmUA4zEF0wB6UaAG76OmjgAkS3sbgo3jb2dXt77LresQZHTZ6SwTnfCeDLAO5hjD0AYIRzfmOxGoaMNvcAeIQx9msADMA1NWvw+f4bQxEEsY9x1YqamW5ewRwn1zGBiF0ZyvSzKxFlSisBfHxIpcS2zFF8KBRENNFBOkM2G5BWUrQxPy+CnVobjgZHcSLMYVIygAQGR45TMsL4EFVs+qZLtLeLTWRibuYT9Hfd1iZM7aM5zOCcX88538g5fyPn/Lzi747nnO/igs8W338T5/wTnHP/fCrXqIv9UrVZb0gQRJ3xnp/UugVNLJgdRKIABFeYiJLDbDNNn6QP0kYUH2Qibpi0EtkeA74iqngO+Z48tsJGnIGFo76OlX7jIDdXvqf1obVVDJDi3K8O6lUH5cMDwodMxmfr6hB/E62tYixYYSPs4KiJBXPD0Oa9SQiC2Gc55P2l17+qTeWM5hbMDhZR9fQYas66yM0NU/83lxOL5nzOL9tZYSPIB2kjTuS0owMdHTDXeg4xTe+balA8h3xPK5hDDizS6VLZ5iU8swlJ5jDHXeAZZnBk7GvGQv9NRL5f4whmz/0K+PzdRUmDku0KGlg0fw5zfZPZXXr9N6aSMgRB7NM88o2amCXBDMNituKDtafHR6TJYwNsGPNaqxSxkz5ErfUclIfNmI/YjOtDKgW0tAQL5iiL2aSNsBHmKH0ta8GFTcnQdpIgTAqR8X5VbfgQlIfd2Sm6JOn7VT22wkaUAR5QJsqNm8jsAykZdc1Vy2vdAoIg6pXP1Pb/cvMK5pDT9MbFbEq0y1cwO8oJjRqx860vrPiQz8crZ+bng7SfWNSRMWeCuYIwud4hZhNkLe1YKRmA7w5zYSPMcQWz36I/38FRiOsU9n6VbdHaiOKDnKkJSskgwVwfHH1x8DEEQexbtHSUXl93RNXNN69gdiSijAIknRaJkj42jBUBlOisb63nEKkAYUWUemwZUXOYlSg54BOxs8hhjuxD1Gl6WV84bPqNjw35Oa0PjAHt7cmmMyj3ay4XfXFkUFoJkNDgKGyEOURfB9U+B3x8CJl+QyRAdk/p9Zu+WLt2EARR/4w9UXWTsQUzY+wDjLEHGWMPM8a+pnn/Ls+Xtgi+c0JO3WpzHT0iyhixC3h4+4qD4udTKRHlrtkUd9QcZkX0AyGmuKNcJ48QVI+tsBFFCOZyojxHsY3d3dHz1X3zsDs6AMacVJhobdXkYTscHAVFmIF46Qw2OcxO71eN6KcIc51x5bJat4AgiHrnvNptXhJLMDPGDgRwCYC3AdgEYA1j7H2ew9qLJYvk14NxbIams1OE2QIWzFU8WPN58TlP1FG7F0OAAAkUzEGRzZACRO4YXEZYARI3r1URtHF8UNtZZiPMQrC4aSVhZxNCiH6/BaTptDAV5zoZc3MdDCzC1MOWNnx9iDqIdJjD7JeHLW1E7QciYV7x7lq3gCCIeiXdWnr923+squm4EeK5xEcAACAASURBVOaTAdzIOd/LOecAvg3gVPkmY6wFQD9j7MeMsXsYY5cwxqpTWDNkdQZjuTTl4c254fkZUjD7lUuTNqLmSUtxoF3MVmURFccHILhaidGHqHmtnih5nMWRYUS/akN7fnm8Ae396rER5zrJethJ3q81y2EO60PI8ntEgrzvllq3gCCIRuDui6pqLq5gXg5gl/LzTgArlZ97ANwN4GwAxwNYDeCvvCdhjJ3NGNvMGNs8NjYWs0lFQubOhhGC8litDQcR5u5un/MD9qJf2nDgw8KCyMUOEpuBPjjIzTX60NkpZga0hXtLnwvT18bBUdT0G0UIAvH62kmEOU4KUVBfWwyOurs1NpLMYdb4MDurGRwxFsoG4ZhLvSN+giAIA2f8uiZm4wrmEZQLZLm1KgCAcz7JOT+3+L0A4GcAKnKYOefXcM43cc43DQ0NxWxSkZDTw2GmbuWxWhtR6gtns6VpfsRPZwgqoZWID7YpGQE2ZJngChuKwPH1QW2ThrBpJUC0tI8wJd/k+3H6usKHfF7kYjtIv/H1AQju65Civ6MDaGnR2LDJYfYpvxd2cBSncgxBEARRI9YcW3rt8yxwTVzB/AsA72WMycf4WQBulm8yxlYxxj7L2FLCwMkAHolpMxxRxaZGHMhjtTZiLsiT78cRgmEqfajtqbDhKA87rg9+aSUtLeKl03QGTZRctqeCkBFmv1QDIIG+tp0RcRBhTvp+DRwcFQrG2YR8XpS+TvLvmkiQ88xlFQmCICq4rHrF3mJZ4pzvBPBlAPcwxh4AMMI5v7FYDUNGm3sAPMIY+zUABuCauI0ORVQRZRthTjKvNWQ6Q5hyaXF98Nu4RNqYm9MsjkylxB7FMaPk0kaUdIZCQUREa9bXYQZHUdNvEhjgBUXi46ZkBFWmaWsTX1H+JuQ+MbFmjkLkSRMOySnXOu3dz5wgCKI+8E6MWsM5vx7A9Z7fHa/8+NniV3UJeHjbLGYDfB6sk5PGJoSNOgYKkAARdcABnl/KeeZq5GF7ooLa6F6IyGZQHrZsQxShlsmI/g6TViLbU0GcHGblBujuBrRp+tWIMEcV/dmsSB9Kp5fel/m/ZbMCLS3imKg598rAIrDEXzaLpZ1gwvhguF+N6TGUw1w9rvButUoQBBHA+Tngq63BxzmkeTcuCYjYBS5mS3oRlcO81iBxILf+Nvogd0HTEJjD7EioBS1mkzaiCGZfIah83kX+b8VitrA5zFFnEwz3q9FG1Hx1z8ClUDCcKkpfe2ZEpI0okfjAPGxHpRYJgiCIGpJS4r1VymNuXsEcUkSFnbqNsxBMWxEgybxWjzhIpYRojrIoz1dsMibmzhFfMGun6R2lrjjp6xAR5s5O/8Vsvj6EXKQapvqDPFZrQ4bbDeeXbazwwSP6A23Y+OAp5ShtRLlONnnY6vEVNkgwV5/zc7VuAUEQjUiV8pibVzBHjUQZpm6jioOgigDSRiajCfI6Ko0HJBCdlVHy4px83LSPJFMynPV1zJJvsg1RfDDmYXsizC0tYidAXxva0hDhc+7jLo4MyoeXbXA6OLKNxJNgrj6p2BmCBEEQidG8grka0/RxcnM1EbuKh3dLi/gy2JB52EGLtKSNKFPcNnnYWh+AaGJTTtMnGXW07euY1R8AcZ20iyMDhKC8rrEGR3H6Osz9KtsRdaGtw/s1diTeMKggHPOzU4OPIQiC0PHBu6pqjgRzwIO1s1MEUZ2mGmim6QF7sTk3Z1jMZhOxixth9vgQNf+34vy5nFCVDoVg7Gn6KIvZNGJTuzlKW5u40aKIWcBZrrd2m3VNpF9tU4WNmClEvj44mjmKMxAmHPLczcHHEARB6Fj35qqaa17BHCeapnw+lQrYnW1+3pgTGmYXPiB6ZDNsRQB5TFQBErSpSCgfoubmeqKzcUR/UF/7Lo4MEWG2GRxV2JAXOeYATx4TJRIv79eKetge0R83JaMmEeZstjRjAxLMdcfAQbVuAUEQjUw++TUQzSuY4+a1OhAgNtP08nitjWqIKB8b3d1i4FCGbZTctrxfNaOORRvptM/iyChCkHMxoHIgNp3cryHyf2MP8Hz6OpcTlyNWDnOcGZGwKUSUw1x9/nprrVtAEEQjc3nyNdybVzA7mqaXx0SNdhmn6cOKTR8RFRg5TdIHG9Hv48P8vFjsGLYf5uY0iyPjiKi2trLRgK9QC6gwEbQgT22D7cAiMA/bUUpG2LQSwKEPCeRhB6UQ+S6OpAgzQRAE4aF5BXNrqxBCUQQIY+LzKB0TVYAYy6U5yP8Nm68pj3Hug4Ooo60QBEq7uZWdX/2MjQ1Pwq5v+g3nIkyqIcwufGobajKbEEJsxu7rEAM8G9FfMT4J4YPcKbDChievyPc6kWBOnszuWreAIIhGZ9WmqplqXsHMWLTorBQHSiJnItFZB2W6qiGifBezKeeXl8xZlNzgg/qZCh98xGY6LSKKFTbCiqgoAwtDpF/rAxBvNsHB4Chszn21Uoi0iyOj3q+GvjZGyX028yEccdXyWreAIIhG58wHq2aqeQUzEBidNS5m80QdnQoQw65mQALRWUc5oWFSMnwXRzoUUepnlpCLuQLEbMViNhsRFWVwpBGzUcWm05z7mCkZUetVR5lNqLDhyAcgYDYBoNJyBEEQ9U7Fgz059lnBHHYxG+BYgMhyaWFzQuNEZz02slmxHXhsH+TxnuvkK0CSFFEBNsKWfJM2bPt6YUF8hU2NAewXm/lep1SqbHecpGdE0mnxY1QfnMwmxPRB2ohynQiCIIh9j+YWzAFCLckHq6wIECtyKo+zjTr6pAJUiJyoea22YjOb1S6Ys42can2QxzkQ/VH62pnojxKdNaQQRV0cGTs6G+d+DXOdZHJyzDxsaSNKNRHCMedur3ULCIJoBl5ONj2juQVzFBHlKOooRV2YvFa5w7TzHGYladf5FLdtTihgJzZ9orNRrlPsKLnPdbLNL1Y/U2HDpx+Mi9k09yvgszjSJg9bJhLbLpjTDI6cpN8ErE2wnU2Ikn5DOKZvXa1bQBBEM/Bvb0z09M0tmANElLNIlMaGTQULxkKUMzP4YFzMJlW44oP8TFgfpB9hFv0BIXJCo0RnHeV6x46SO/JBbo5im85gu5hNbVfZ+dV2KRjrYS8slH9WsWHsB85Ln1NwGolPOoVIbRdBEASxz9PcgjlgethGgORyGg0QIuoYRkTJ42y3xjYuZjPkYavtWkJuyazxwSiiAGeLI51EHQGn6Te+UfIoPngWR3Z1RUvJsBXMFX74+JDJiNT6MP0gbUS9TmFz7rU+yOOSTLUKKFNIEARB7Hs0t2CO8mD1meK2idjZCEEgINoVs4KF2g6bKW7jpiKLi+LLQYWJaqQz2A6OtPm/UWYTND7I45xFTpO+Xw0+RInOyuskq2yU2fBsIBOn1CKlZBAEQexDtHZVxUxzC2aHC8EAu4idTdRRHhdlwVxsH6SNKLm5DqqJzMz4lPfz2IizYM5WbNrk/9qIfmkjihAMm0JkFJuMifydKNFfR33d2SnSiIJ8CJxNiLnRjuqDcXMUWvSXHC/9ttYtIAiiWfiLR6tiprkFc1QBoommyc9UnB+IFjm1yZMuFLQ7zPkKQVsBEjMPG4iew6wt76ex0d4uxJbTSHxYsekoh1nasK30YbuYTW1XGBtRouRRUjKc+aDph3xeDHRsKn1E2RyFcMCP3lrrFhAE0Swse1VVzDS3YI4qQMKKTR9xYFMuTR4XpcJEbNEvbcTML5bHRYk6GvuhtbUsHCkXR8prW2FDc40KBXFdbaKOsl1aH2JW+pDHGUW/THfR2Ii96E/aSDqFCLC/Xz3nl5XybHyQfz8VPvhU+lA/F8aHasIY62aMeePxzUHOO4VDEARR3+yTgjlwMVtYASLLUzgQUYECxEZsJi2ifKLk2axd/q+ND9KGTYWJTEb0t21k0yiiHEVnbRebOY3O1uPgyOOD786Rtver3LHPQTWRJGGMpRhjH2KM/SdjbBTAMwB2MsZ+zxj7KmPslVVtEEEQBLFEcwtm28VsgK8AqYhsplKBOaE2YtNWgESZpjdGZx3lYQN2ud6+edie80sbNtP0RjFbKIgbwWGEWbuYDbDb9ANwNjhy0tcBKRmFQngfbHLupQ2tD4bBURQf1M8tUbsqGXcCOBjA3wJYxTlfyzlfCeBNAH4L4B8ZY/+z2o0iCIIggJbgQxoY28VsgPMFc06m6QH76OyKFWW/amsTGQ5OFv35TNPLz/X1ec6vfi6MD5rUGCDgOjkauKifKzs/YLTR1aVZzJbNil+2tlbY8K3OYBCbNrWkAbuSbFEW/cm3ywYKAfdrf384H6QNm1KLUlxHuV/LqF1Kxomc8xxj7BHO+evkLznnuxljL3HO38cYa/U7AUEQBJEMsSPMjLEPMMYeZIw9zBj7mub9TzLGHmKMPcYYOy+uPSs6OkQo2ZMTaow65nLieEcL5rQVAaIsBAOMQs0oomzFpqNyaYBdTqhNXqu0ESXVIGwFC6OIamkRX7YDF9soudq2Ivm8OFXY6GxHh5j8SHLRn/E6RblfbfvaUR52lPSbhHkvY+wfAfQyxg715C9fAwCc88rVv5bU9f9sgiCIOiWWYGaMHQjgEgBvA7AJwBrG2PuU948B8EEAxwB4A4BTGWOb4ti0wvDwdjZ1K23YTqGrbVNszM9rimEYxKZczOZMqDnKa1U/V3Z+9XMeG2HTSqQNXxHlqRHmTERJGzFTY3x9MFwn42I2eazHh8CdIx2KzZr2teb8atvKzi8/5zm/+rmy86ufqx73AXgKwCCAKwA8xxh7hDH2cwBO1Hvd/88mCIKoU+JGmE8GcCPnfC/nnAP4NoBTlfffBeB7nPMFzvkCgOsAvCemzQo+/3ng6KM1bxgefM7EgbRhG3VU2+axETb/13cxW40jdrYl2Zz40NmpLb/ntK99xGbYdAlARGczGZ/FkWEHeD42oqSupFKaUzkUm1FymJ2k39imZLS0iKmhKgtmzvlLnPN/BfAezvk7OOcHATgRwOcBvMWRmbr4n00QBNFoxBXMywHsUn7eCWClxfsAAMbY2YyxzYyxzWNjY9aNmJwEnnpK80ZAhDlsrmNLi3hGO4kwa3Y1A0oP77DpDMYpdHmsRoD09tr7wJjIz604v9o2jw9Ooo5RRJTatiJR00pshZptHjbgszmKwYeK+9Ww46K0EeV+rdhmPUBs2m7m4ywSHyUP20Gud5IwJq4+5/w++TvO+W7O+cOc81n1mBg4+Z9dbEus/9sEQRCNRFzBPILyf6arir8L+z4AgHN+Ded8E+d809DQkHUj5IO1Yscuw8PbVkSpNirwic7a5mvKz5VhK/rlsQ58kBHBsCLKKEACyu8lmc5gG3UMzP91lMOstq3MuI0PPvercXDk09fGKLnGhu39urAgvpzmMHv+4AP/rh3MJiTMnYyxTzDG1qm/ZIy1Mcbewhj7PoA/j2nDyf9sIP7/bYIgiEYirmD+BcRCFfkYPAvAzcr7NwM4kzHWWlzA8ucAbolps4KeHjG9LcutLuEoJUMea7uIyomIMkQdjT7k8yItwWHUsQJbAWIov7ewIJoaJcJsHBwZrlPY2QTfzVF8cphtUjKiDo6SvF+j5NyrbVvCMDjyzcOOklZSKFQs5jWW9zP4IGdOtDZWrRIzQdXlZAB5AD9gjL3MGHuKMbYNwHMQecX/xDn/vzFt1MX/bIIgiEYjVlk5zvlOxtiXAdzDGFsA8GvO+Y2MsbsAnM4538wYuwXAAxAPgh9yzjfHbrUHKVZmZjzP3agCxPbhvWdPxa9nZoADDtAcHzBNn2TUMUqUPEoedlgbvmklPoJZDo7KzDu+TjblzGyj5IHpDGEHRwE+7NpV8etogtknhSjs4ChqX/um32QyZSX7ZmZEUyt0ruE6pdPCrNbGE09ofpksnPMsgKsBXF0sH7cCQIZzPunQRl38zyYIgmg0Ytdh5pxfD+B6z++OV15fDuDyuHb8UIVaWflh2wizIXIqj7XdCMJGHNiKKNutt+WxRh9kST2lDp5t1NHogzzW0WI2+Vnt4EjT1y0tGhEVJTobJYdZ80bUwVHYKLm04WRwFNAPYQcWxr7m3NeGTOUo6z+1r5WC37b3q7Sh9aGGMMb+G8BnOOePJ3H+evifTRAE0Wg0xU5/8iFZIQZ9cpi1i9mqIaIc57U6E1GAVuQYRVQ6LZSo5zTG/F+NUAvMw3YQiQ/Mw3a02CzJ9BunOfednUKBekp0OMu5l+0Je78uLAjRbFikCtgthDX6ANj9TdSWCwD8E2Pse4yx1bVuDEEQBNFkgjlsiStjRYCoAsR2EZWPAKkQ/VGj5D6pBmG3M/YVIBoffPN/E4gwa33QXCffxWwxB0eydrZtWTlfH5LOYZYNV7CtJS0Hm7H7OuB+VT+7RJQBno8NrQ81hHP+COf8LQB+DuCXjLHPM8YqO5kgCIKoGs0tmH0ESJSp27CLqOQ0cpSoY0U0Te4w50hEca4JiEe5TprzSxuxUzLkNL2jXG+nfR124ALYi/6A2YSKxWwhhGDF4sgo10lzjVKpgN0pHS20VT8bywcfG/WWkgEslY/bAuCbAD4BsYnJh2vbKoes/KNat4AgCMIKEswqjnJCAysC2E5xa8SmbQktXxtRInYakSZt2KZkOPHBJ8Jss3BR2rBNNXDS14btt42L2QLu10JBM/lh+zcRta8dlXJUP1t2fvWzRZz2dQ1hjN0L4CUA/wTgAAB/AeB4AG9gjF1Tu5Y55H1UeIMgCEds/UVVzMRe9FcP2ApB25qz0oZRzM7PC3VSrCTgK6IMEbu2NqGVbMSm72K2gMjmfvt5fFA/q9iIEmEOK/rjTNMbRZSNEJTt0thIMsKsVnXR2rBJjZGf8aD2ddnbmoEF59Xra9uce/Wzfj7I47TlgLNZUblDs+eHsZpIbTkHwO+LO/GpfIIx9nQtGuScvnXBxxAEQYThp++sihmKMKsEPLx9tzNWckKNO7NJGxoRxZg43iYntLc3/KYi0gf5Wa0PGhFlk8MM+PhgE2GOI6IMi/4qyGTExdPU2vXd9MMQObXp68DFkbaiP2bax9yc6G+bPGxpI/bAwmEOs23OvbRRhznMT2rEsqQ6TwaCIAiijOYWzI6nboFwWwFHmaaXx9tEmJ2JKI0P2awYHDibprdJK3Ek+uVxvmLWEHXU5v/alkurKBYtkIsjbcRmlAGe2r6y86uf9fNBHhdlcGSIMNtWplE/W3Z+9bOKDdv71Tg4qlM459tq3QaCIIh9kaYQzMYdu1pbRfkzmwerzCP1YCPUogoQ2yluZyKqGj74RJhtF7Opn10iSm6ujw/GnSPlTooeHypsyA9HuU7ViDCH7WuHg6OurrIy3059kMc5u18JgiAIQqEpBLNcsR9WqEWdugUcRewcTHH7phqo7fKcX21f2fnVzyKEiHIk+ru7KzaR8/XBODhyLKK0NjS5s1FSDQC79Ju4OcwV51c/i4QGeDaRfrVdnvOr7Ss7P1BmI58Xp4riQzZbscs2UU2231HrFhAE0Qx8bGeip28KwQw4is4GRNPkZ8uwidjJaXpHUccoCxdj+wBEE/02aSU+qTHGwZGm/F6hIFJoovgg21fhg9o++OQw+/ggbcROyYgTiU96NsFBlNxYr9pxlByoz9Jy+ww/fGutW0AQRDPQsyrR0ze/YPY8vONUBADCReyMIsqnMoM83hh1rHJea+BitgAftPm/DipYAOHFZuBithpGmJ2IzUxG5Di0tob3wUb0A4Fi02aRqq1gTqfFqcL4YKzCIY8L6Ot6W/hHEARB1BdNI5iNi3c8IiqbFZHHJAVzzUWU2i7P+dX2lZ1fbR/iReyM9X9l+b0YPkgbYa5TnMip+vmy86vtU46pWMwWR/QnOSPieNHfzEz4xZHO+tphzr1viT8iWdKVFWoIgiCsWPQuNkqOphHMYQWIsTID4Dwlo2IxW1QhaJPDnM2KvAXNwkVjOTPHea3q58uMA2Ur6aJEHaWNMNcp7jR92AizNg87RA6zTV87z7kPm0IUcJ0WF8WulmV0dIhfKjUYo9Q+lzYqfGhvD++DPM62r4nk+Yx3y1GCIAhLvqb/354EzS+YPbmzcaduw4rNzk5NRQBHkVNpw9cHTbk0YzmzaghmQ9pHo0eYAxfk2aYzeHxYXBS3r60PgYsjw1ynEJU+tDYMotxZXzNm/Lt21tdE8rCmefwQBLEP0DT/scJGmJ1P3WoizL7RX/UzHnp6xOIjJWuh5INyft/FbD65udJGhQ+trUKEOIo6AuG2M45SOcHogzze0w9aH6SNJIWgoyh54DbrhvMbF0dGybl3FIl3ep08A4soG8jI88v2ETWkQGVKCIKIQcdg4iaaXzDbRKIc5oRGEYLyMxUr9j3iYG6uvE0VNgw+yM9oI3aG1JUKPxYWhGi2HVgYrlOSIsp3NiFgMwsg3PbbcX2oyP91FCVXbZTR2irUtOdvIp0uZTqUnR8I7OtY1ymTKdVLD+uDtGHzd23rA1Fdvlq5cJUgCCI0n5xI3ETzC2ZHEea2NvFcD5vDbFsuTW2TVmxms0vqyrmIkm3y+CB1tNaHqOkMYSLxjiLMiaWV2EROfWxwXpFp4yznHjDkSct0Bo2YrcjicRhh9p11sR3gSRuUkkEQBEEA2jRU1zSVYDbmhGqm6W2jjtKGk8hpFLFZKCztMOfcB9kmjw/d3QmIKJtIfEXIM8AHQ3S2YvGltGHoB5kCnmQOs28kXjM4ss25B+xSV6IOXIw+KJ9fWBC3rm26hK8PSc8cEdXhHdfVugUEQTQq//2/q2quqQRzLqdZsW+IMNuKKGkjbOQ0am6u2sYlPALEuQ+AdmDh1AfPdZqfF/3lK3AMI0bbiii2A4vA/F9NlQzt+YFoud6cL93IUYWg/EzYgUXUhYtqG8vOr3ze936NknMvbYSJxOfz4loabBg3RyGqwxF/WesWEATRqDx8VVXNNZVgBgwix8GGHNJG2KhjnJSMChHlEWrOfZA2wkROowpBg+iP6sPCgmFwFHY2wWFfx7lOQYOjavW10xkR2/vVQYR5elpMSFTs4RLgQ0uLOBUJ5jpg7wu1bgFBEI3IsldVxUzzC+akUzIYE0/qMNUfQuz0Z/QBCCei4kQdHVSwCLvoL05urvxM0OLImRmRe97m3R8hlxORR1uxaYgwR+lrW7HpNF9dk/8bp6+DFv0F3q8BPmQyZSWd7XwIGLjIdtGivzrgWxtq3QKCIBqRj2ypipnmF8wymqbkhKbTmuenXIGVZMQubkpG8eGfWF6rAx+Mm6N4UjLi+qCeo8wHB+X9pI2ggQvnCeQwG9IZnEdnbfKwHaUQRfUBMAyOHORhSxsUYSYIgmggdj9XdZPNL5jlgrlFUedTPlgr0mMDNmmQNoLEpq+IijpNb4jYxYk6asuZOYjYhd0cJW6lD/UcZT44EILShrYkWzq9dA0yGZ9t1n12XPT1wSYlI2r+r21KhqGvjZuj2KRkhPBBayPpviaqxwXewvMEQRABXFudNAyVyIKZCb7CGHuAMfYYY+wMzTEtjLFxxthdypd3gtwJYVMB4kzdhklnmJ8X08eJROzCCpAAH7TbGYfNYY4qQDwR5rg+AOEqTDiPOipCLVSdZ5+Fi0D4fHWnCzwdpWQYF0faDPCi9rWjAZ60QYK5hqh/IxPVmVolCIKwJU6E+UMAXgngjwEcB+D/MMZWe45ZC+C/OOfHK19eqeaEsNUZEolEKWIzMPrLmCapVhA2JzSR6KyjlAxpI+yiP+cRZk/5PeciShGbiUVOgbL7qatLs69HyBQi7eJITXQ2yb6Ou3ARiJF+QxHmxuI7h9S6BQRBNBIXeqfLkyOOYH4XgGu4YArATwGc4jlmPYCVjLFbGWO/ZoydHsOeLzZT3E7zWuVnbCKnhqijcXMUTdSxo8Mw218HETvthhmGCLNR5ESNMHtsRB0cGReCKWKzGj4Y+2FxUQwOouT/KmJzcVE0NUoeNmDoa5uc+zq5X2nRX4058K21bgFBEI3Cf32sJmYDBTNj7C2elIq7GGN3AVgOYJdy6E4AKz0fnwNwF4S4fheA8xljh2lsnM0Y28wY2zw2NhbJEZsFSHEjzBX5v0p0Ns5iNtVGGZqoo/b8IaOOajt1PhQKQmQlkpIRNp3BQXQ2kZQMRWzGEYIdHSJqHKav4/igtrPMh+LnpZiOUulD2oidcx9VMFMOc/Nw+n/XugUEQTQKj15dE7OBgplzfocnpeJ4zvnxAEZQLpBXFX+nfvYBzvmXOOd5zvleALcDOEpj4xrO+SbO+aahoaFIjlQrJUO7nbEmwhwl1UB+LnLUMZcTajeq2CyeX4oop2LTU34v7sJFrQ9hI8xxZxMclPcLuzgy7v0K+IvNwH6Qx/vY0C6OTKXKbGgr0wDRB0ee6jeUktFEXJr8FrcEQTQBf765qubipGTcDOB/AQBjrAvAaQBuVQ9gjB0j0zAYY+0AjgfwaAybRow7doVNyXAUsYtTQkvaiBxhduRDYM6p2iaDjaBc75kZoam0TQ0QzDa1nuNcJ+POkWFEf4AQlJ8LWvQXOCMSZ3EkQm4qYkghkja0gyNPJL6313CaOKkrxR0ROXczc0QQBEHUOWNPlF6vqoi/JkocwXwjgJcZY5sB3A3gHznnOxljRzLGflg85mkApzHGHoJIzbiGc/5krBYbSKfFMzFM/d9EInYOduGTnwtTOcG56O/oEAmti4tOBHOY/F9teT9pw8cH4+BI09eJXKcqD458c+6T9CEgSi5thO1rLXEizACQyWB+Xty6cf6us9mlypNEraDycgRBBHHdETUzrS8SGwLOOQfwGc3vHwNwevH1bgAfiNw6S6o1xa0VtA5qJMvPhcnDXrbMcH71eMP55Tm0NrJZzMz0lB1bYaO9XYSHDWgXgkkbQQMXacPHB+N2xsp1ktUhXAyOyq51ZycwOQkgREqGthZcCd8Fc8r9TyyF5gAAIABJREFUdPDB8X2osJHPA7kcpqdby46tsBFigBemcowxhSifj7c4cm4OM4sD/j6oxxt8kDYGBoyHEUmjjp6/2gqcn6tdWwiCqG9O+FrVTTbNxiVAcP3fxUWhY5LMCU100Z+jPGy1nTobcaPkYRdHGqOODhZHBpatk+3xOb9sZ4UNB/WF5eci56s7GxyJl07vV2kjyIcQUfLAyjGZjJMZEdlOok4oULifIAgPw78pvX7Dp6tuvvkFs/JgDSWiHOWEOo0wp9NCNYTNww4ooWX0oXiOODWS5ecKhbKqX6V2BaWVhIg6Sht+QjCUiIpZ/3dmRgg6bVntkDnMFedvby9rY5y+DlNNJFQOsw/GwVGYlIwQPqg2yrAVzFH6mqg+lJZBEISJ64+pqfl9SjAnKqIUcdDSUtI9FTaiLAQDKgRIVB+M2xnbiKgQPmhteCLMUX2QNmL5EGAjbITZmFYSNf83lRI3Tybjv5jNIofZLyfexcLFoJ0jA6uVxExTChzgyQGnz/kBEsx1gZqWQdUyCILQ8aG7a2K26QSzcZc8B1FHY3S2o0MohkIhuCJAnJzQbDa2iJLbGYcRUXEFs7YvHCxclDbCpBrEjc5qr1NQaoy0ESVyKtuVzWJuTkRuo96vYSrHuEjJAPyvU5xKH9JGrIFwVB8IgiCI+uC6Pyq9Xvv/2zvzOLuO6s5/Ty/qRVJ3S62WWrIlL7KxbGywY+FxgBjhEFabJMBggYclwJhJ2DIsNkuYZCZkwJgwbDP5RCwTAgk4GMaGgI0BI9sYMMjGGK9g2WBbbslSS90tqffumj/qlt59791733Lrvq3P9/Ppz7v39X1Vdarue/dXp05VXVCXIrScYE4dkpEyJjRxRYAyH96TkzYqIY/Aszk9bf+Xmdj0EJKRGPbRKB7mMiYuunIW5VFOHHYZHuZSE+bKWiO5msmREfUUOT8xTVuXE5JRxnrYUMf7VakP4a1uRx+sXzkURWkc9t9d7xK0lmAutSVzSRElEhOQail3wlziMH2Z3q7JyYJ/BB67tF5yl0c59ZRmmB5KL7+XpYfZRyw5lI5XT9vWSZMjS67CAdWJ8oJ6Wr48pu9QppccqqynMtu61GoimYUQtRhi+bCI3C4id4nIpRHXdIjIgYKdXeN/FLPmc1vqlrWiKA3CYsiDWMd5Di0lmCNFVEeH/St3+Dlhk4bubissSnm7ql0uzdkA8R67kjaEy5OQRykB0ttrQz8j82iCGGZfoQaRNoTWq47donx6OiaQPT+PpJ0ja9HWifdrms5R0NaJK9NU4GGODSFSwVwJrwZOBc4HLgA+ICLrC67ZCNxYsLNrYYR69rzhV6WvURRlaXBVaAXkBI2WNa0vmOGYAEnrOY3dzrjAOxuZvlNGKWNC0w7Tu88m2eBjyTeIj2FeXLTbb1e7IYfLI8s47JKTI5PqydngEomh1Lrembd1kIePti7VwUvb1lWHZKQR/a3HRdjNo4wxZgK4BnhxwTUnAmtF5HoRudXt1Fpzhs7MHevkP0VRAJ71N3XNvuqNSxqR8I5dHWHLyhniLkMcuDxKeWfXrYv44OysFc0pY0J9hWQEe2/kKLAhjZe8VAyzm8zmXQiGlt9LG5LR3m71bnJbr0gdagA2j7x7ppLwmzK82KVCMny0dakOXtaT/tKsTOPit1tl0p+IXAj8t4h/zQJ7Q+cjwNqCayaxu7J+GFgB3CQidxtj7ovI5zLgMoBNmzalL7iiKEoh4Q7zs/+6fuWgBT3MkCKcoVrBXOB1TCsOID4mNLNh+nJscHmkHKb3ZcPUVMzkyMCGtraYZMqIzXV5lFp1Ja0NUOX96kI+EiYuujxKha6kXRoPqmxrjx7mNCvTdHTYS1rFw2yMuakgpGKbMWYbsI98gTwcvBf+7O3GmA8ZYxaMMePAD4BzY/LZYYzZaozZOjQ05N+Q8OS/6+rj6FYURXG0lGDu67OvExMF/wh5u0RiRsorEMyl4inTek4hxTB9iYmL7rNV2eDySBOSMTvLxJgN2s9EbIbqacWKGBFVxjC9K19SPcWGZLgZm1mHZKS9Xz2t6gIxbT01xeEJk3ddUfru2hJ5HDliN8M5hsf71eXRKh7mBK4D3gggIr3Ay4DrwxeIyLNcGIaIdAHbgF/UtpgRPHB1vUugKEqt+d7bcsdXFM6Orz0tJZj7++3r+HjBP8oRUWU+WPv7Y9IP0kg7mS1W9BfEYVc7cRFibCh3pY8y6qm723rtIjsuwPj+2WPliEw/dG0csW0dqqc0Nrg84uppZmKGubmM2rrccIYybOjrS75fY+spmNiYyobFRQ6P2SGANB5m19Z5graz08bNeAghAmtHkQ2tx9eBJ0RkF3Az8BFjzIiInC0iXw2uuR94mYj8HBuascMYc099ikv+Q/LX19atGIqi1IE7P1PvEuTRUjHMtRJRu3dHpA/MHp5hZiadiCpH9EM6EdXfb8XB4mJoRL9ARJ18csQHy5y4KGLzKIqTDurJCububASzq6eFEm29tjB0MzqPOLF5eNSK/kzauiBePdY7W0ZYSWLnKElslun97emxnaPkeupIlUe4nvLumdB3IpPOUYthjDHAuyLevwvYHhwfBF5Z46KVx//704bwMimKUgPu/7fccYN875eUh7nogRvGg4d5/OBCXjmK0g9dG8fAgH2NFJvT08fydp69ojzKtMHtGHiMzk6rdJPqqcyJiy6P2Ho6MHfsmkgbQtcmpQ/xYjOztnaif3Q+rxx5lBmS4T4bOQEzsKG3N2ZX5zLDSgYGrGc2MpwhuJ8ibSjT++s6R7H1lNTWZS4rF9vWvb1e27qoHZTG4PLQRIU9P6lfORRFqR3fvKTeJSiipQSzE5FxHuaSD9aUHrvxQ4vHrolMH0o+vBM9doE4WL68YBUQR5kiKlKAiBwLBYitpzJtACvU4upp4pB9AMaK/jLySOwcldPW1Yooj52jUiMivmwwpiCcIVhNZO7IDFNTftq66npqa4vpEeTbAHXoCCuNgYQeU19+Zv3KoShKbXjwG7njywtn9tePlhLMtXqwunCGvPTxI5gTPXbT04yPGS+iH6LrafbIbGkRVW3HohKxWWK5tLp7mGvUOfJhA0Tb4d5LK5jLaevIzpFbhaOMmHvItp4iO3hK4/CeudzxQ/9ev3IoipI91748dyyNI1MbpyQeqJWIKgpncCJqIr8cRelDOgGyuFhaMKcVUROSd01R+q4sZeQRKzaDVTJiPcxpRZRH72xcOIOvzlGkUOvpgdnZ5LYuY8m3cPmi8khs6zLDJdznk9o6Nqwk7f0aCOaxsRgbFhZgbk49zK1AW2hI7esX168ciqJky83vyx3XcRvsKFpKMDuPXdyqA7EPVkj38HYiarwGYvPQgjcboobRxw+35V1TlH5wXTl5xHodxwwrVlS/9Xa4fHGdo9i2LnPiosujKJzhWOcooa3LjGF2n08Sm5l2joK2dnHzRelD6rZO/M55EP1zR+2ISKINZeZR1DlSGovww/O7/6V+5VAUJTt++pHccR23wY6ipQRzbDhD1kPcQfhATQTIoYyH6Y9YFZulDePjMd5ll0cZ6SeFM8xOLTA9HWPD3JxVRSk7R2NZdo6OdSxibHB5pPTOjh3pyLumKP1QWUrlEd/W4s2GyA5ecL/6sKGoc6Q0FuGH513/WL9yKIqSDeFd/RpkZYwwLSWYId5jlyiiFhdhZibdhLnubsaPZOiddV7H8WxF1PhRfyKqKNbbTfo73JZa9Cd1jnzaAAV5uHbw6ImPmzA35mmSKqSop7QhGYcltQ3d3Tako+ZtrTQe4YfolY3lfVIUpbVZGoK5p4fxqWXH/l/EzMyx68pJH6IFwtgRG6iZuPpDGQIhNq6VMgRIWg/zZGfeNUXph8pSKo+iWO9jNqQXzBC/Esf4dNexMkSmHypLEonhN0fa4lcr8SU2JxLaOs2KKEEe45MJYrPMZeUgeem68cPtyW29fHnJ9BM7Rx7vV1DBrCiKUhca3LsMS0Uwd3czTt+x/xfh48EaPLxLiqi0Q9wexGZSOENix8KXd/ZoCRFVpmCOFVHTfmxwnvy8PDo6oK2N8aMd8TZMTtr0y4i/irNhlk6mZ9K3deL9OuWvY1EUzuDu16S2dvVUBlV1hFUwtybqZVaU1mL2aO5407a6FaMUS0Mw9/QwTv+x/xdRxYM1Mp5yqjPZI1jGmrMuj6hwhhmWeRFRSUvX+fbO5tXTMRGVIDbL9Jy6PCJtmOnJK0MeaUVUsF71+GRCW6cV/d3dyfdrBXkkhjMEbZ1mPexwGaM7Rwn1NDlZ1sRIl0eSDSqYlxgv/r+54ydur185FEVJz/8KbWf7qh/WrxwlqFowi0iXiLxdRG4Rka/EXCMi8mERuV1E7hKRS6svanlUJUB8PFgDsVlS4JTpdYzy2PkSUS6NSAEyY4VO7Lq5wXXlpA8xImpyWepJfy6PyMlsJuPRhO5uxibLaOsyiFydoVRbu+XSygj5SNqmfHymK3knweC6cmyA6M7R2NSyTAXzWHC/ZtYRVhqTs16fO/7S+XUrhqIoKfnC03PHbz9Qv3KUQRoP8zzwAPBhIE4Fvho4FTgfuAD4gIisT5FnSWIfrAwc+38RFTxYE8MZpru9iSgoFpuJIsqY9N7Znh7GZnq8hZVAdPzvxLQ/72ykEMy6cxSEfSROvqxACBpTsBRiKcFcQcfFpRFpw2xvcjuUmUfc/TpLJ9NzHfH15MPDPNubV4Y81MPc2oSXmdPQDEVpTvbfnTvuGaxfOcqgasFsjFkwxtwITCVcdhGww1gmgGuAF1ebZzm4cAYTjhkPCZC0y6UlhjPM9mQnmEvZUMHERZdHpA3zGYqori7m6GByLsHr6MNL7qmtY8MZursZn0noHFUQmxsZJx0S/WltgIR6miujratdiaPcEZG0gnlxRXweaUdElMamcLRuLulRpChKw9EEE/3ClBTMInKhiOyM+BsuI/1BYG/ofARYG5HHZSKyS0R27d+/v/zSR9Dfb4e3C3fi8+V1dGlECxA/grmUiPJlQ2Qc9tzyZM9pmXlE2iDCRJdtfl8hGUXhDKF6ShtWkrg6Q406R5ndr93djM+XaOuOjpihhuL0oSCPtjbGO4fy/l+EDw8z/SxfblKPiMR2jpTGJvyQ/Xh595KiKA3ADy/PHT//H+pXjgooKZiNMTcZY7ZF/O0t9VlgH/kCeTh4rzCPHcaYrcaYrUNDQ+WXPgInkuIESNoJTpBCgDSDiFpckSwEK5i4CMV5HFxm+1mrVyfkUYENcbHey3sXU4sol0dkPZXyzlYgBKHKti7D++vSiBSbCyXaOk0HDxhfliCYjalYME9M2PDtYwT11L8yZnu+CkeOIpcpVBqfvwzFM2lohqI0Bz+7Knd8TnPs3Jn1KhnXAW8EEJFe4GXA9Vlm6B7eed7T7m7GGGBFz3z8dszBdeXmUfhgNd09jC2szE4wBzaE/1+UPqT2kh8yAwz0JwiQMicuxnnsnGAejAtV8tCxGGOAgRXz8ekH15WbR6ENM119TC/6m/QH8W0deT+5rbfLWMPY5REl+g+ZfgYGYobBJicrSh+K8xhL8jDPztqhgQo7FoWdo0OsYmDlQuRnvHwnlMana2X++WRjTxxSlCVPk4ViOLwLZhEZFpGdwenXgSdEZBdwM/ARY8yI7zzDOM/lwYOhN3t6GGWQNX2z0R+q8ME6MACHDuW/d7SjnxnT5UUIOpGUl0dgA8SIzQpF/6pV1mM3H9aV3d2MMsjgQIIAKdMG57ErrKfRzgQPszEV5bFqlX3Ny6O7mwOsYbBvLvpDFbb16tUF9xIw2maFYGxbVxHDXLjCxCiDtMlitNh0grlMsblqVXE7uDwGB2I6RxV4f7u77e7wcW0dWU/OhjRt7Wzo89M5irpflSYh/ND9dLpRSkVRMuR/H5c7fsGO+pWjClILZmPMTmPM9tD5XmPMtuDYGGPeFYRbPMMY8y9p8yvFmjX29UDYyeCE4PKZ6A9V+GBdswZGR/PfGxWbsQ/B7MRkXh6BDZ3tC6xYEfGhKmyAOAGSIDbLTN/lUVhPB9sS6slNXCxT9Dsb8vJwNqzw0zlas6bgXgJG222UUWJblyk2XRqFbX2ANazumaIt6htaoYd5zRob0z8Tuv0Xuno5xKr4tj56tOz0wdpR9J0IOhaunfKoUPQntvXKEm1dwf1UaIPSRLwn1HHS0AxFaTwWZuHIE7nzs/9z/cpSBS23cUnig3V5zCzqKkVUeCWOUWNVrg/B3NlpvV15Qq29nVEZYrD7aHRERJWCOZzHbEcvh+ljcKU/wVwkNgMRFelh9mBDrnM0Hf2hCvOIFILlCOYKvJptbQU2LFtmbeiZjP7Q0WBXpBRic2yxD0MbgytjOpEVeJhdHoX1dKCctq7Qhrx6OtY5SugId3UR3euIzqPwflWaiLZ2GD43dx6eVKQoSv35WFfuuIlCMRwtJ5idiCl8sB5gTbwAqcLbNT+fv3bu6OKqvPyL8CA2D7SvZbD7aPQHPAiQgwt2/D9RbJbprXN5FNpwUFYjLCYvl+ZDRPUmdI7KnLjo8jh0KD905QAlRhMqCMlob7eCMs8GEUbb1jLYdST6Q1V6Z8N5jC7YBogVm1UI5qLOEWtY2X6UZcti0odUNpjuMtq6gu/c4KAK5qbndbtyxz+7CkxMyJGiKLUlPOrzl805WaTlBHNPj30GR3od48SmTwESF//rY4hb1rBm2eHoDzivYwXD9FBgw5ydPBMrmKuwoUhEmUEG2o9ET76s0AbnuQznsbism4OsTvbO9vaWNXERbD0Zkx+64jpHkaEG4McTL4MMLvMjmKM6kaNzdrmYwV4/bR1pw+IqBjtifhg92HCU5czSldzWFdpw+HB+6IrShIQ9Vx+N+qFRFKWmfPnZueOuAeiKW1e2sWk5wQzFYnO+s4cxVsULkKNHrcApc+g2UoDMBwIkzmPnhFqZRHvsBhnsnIj+QIViMyp2dnQ2EMxJnvgqRFQ4dOXg4gCr22NEVIWhBp2ddmWDsA3jc70s0p7sna1Q9ENBW7vRhNURQ0pu22ovbV2inirsHOW19YwNhE9s67Q2LK5isD1mr+kKBbMLXYm0Ia4jXMV3DjSOuSUIb7Gr8cyKUj8m98Oe23Lnf9m8M6tbUjAXPrwPTdkwgkSxmfLBOjprBfPqnojhYbfmbAN57CI9zNNlCJAKbSgKXVnoZ7DtYPQHKpzM5vLIs2HSenZjBXMVNkBBW8/30ctRutsiJptVGCPt8shSbEa3ta2DxFGXCr8TBw/mr5M8Ot/PoMT8OFZoQ1ToyuiU/exg3KhLFd850LCMlqBnEDY+J3euollR6sOnQ1txNGHccpiWFcx5AmfMDsslis2UD9bRmeX0MU7nfIRgnp62ojmFEDTGhn0MtsUIkAq9jr29VtNFCZDVnQlhHynr6eB8H6vxY4PLI1Iwx7W1BxtGZ1YyyGiuvGEqXC7N5RFOf2oKpkwPa+LaenLShpR0dUX/v4BIL3kpsVlFPRWFrsz12XqKokLB7PKItCGpI6yCeeny6p3557u/XZdiKMqSJdxRvbz55xO0pGAujJ114nlNR4zHzoeIml5hxcFkxBB3haEGLo/JyVxyhw/DPJ3xAqTKPCIFSJLYrMITH87jwGwfgyZGkfgQzEesiEzsWFRgQ6TYnElo6wonLkJx6Iq7XwclxhPv7tcy47Bd6Ephx6KdefrbE0JXUrb16OyK+Lb24IkfPRqMHGV4vypNTtijdc1FsBCzApCiKH4Ji+WL/7Xs51Uj05KCufDB6o4TxWYFD9a+PujoyM9j/2QvQ+xP9jqmCAU4ZsPik9EfOHoUli0jej/o+DzybDjSQzdTLF+I8dil9MQbA3sn+xle2BOfPqQS/ftH7S29RhI8mylDMg5M9sZ7mKsUguHQlf377Wus2KxQzLo88urpcBdrOIBMR4yILC7aUZEUYnNuDsZmlzO4EHO/+mjrw1Yw+25rFcwtRlg0fyxqyRZFUbxSGAJ1xqvqUw7PtKRgHhy0O6fNBc6EkWBvwfWyN/oDFT5YRYof3iPjvaxnJFpEVek5hVwezoYNC49Hf6BCG1weeTYc7GI9I8hkhA3GpPbET0zA9EIn6+cftaKskCrqqXCCZ8m2rtAGF7riRCzUrq3XE7MppgfBPDJq2/qYwA9TpZcccnns22dfNyw8Fv0BD4J55Ml2OphjDQkjFikneCotwjtDo0Eaz6wo2fGdN+afN3nccpiWFMzr19tX99B+4gkQFlk7/0T0Byp8sAIMDeXSBxg51G0FyJGIIe4qwiWGgt1dwzYArJ+PESA+bBjtjLdhdtbO6EphgxOCw+yNFmpViM21a+3HXJFHRmClHGbFjJ/RBIB163I2GAMjY91s4AlvgtnV05OBM/ZY52gxpnPks62nI5aVS2FD8f36aP4yKY4qYr2HhmzHxU0sHBmBdbKftqMJcdgVtLXbMChcT0qL0NkDr/hO7lxFs6L459Gb4VdfyJ23kFiGFhXMxwVblT8e6I2REVjXeZCOKT8PVoDjj8+lPzsLB8Y6472OVYRkHH+8fd0TRC8c8zrO/Db6A1Xa8MQTOWfvyJPtXm3o64OVKyNs8NixcPUUbuv1nQeibYCqPPHhtj54EGbn2qwNUTHMzq4K8oi6XwGG5xK8synuV4CR/R3xHuYqvL/Dw3bZt8i2jhLlk5MVhxAdf7wVy+GOxfqOmDAoqKpjcfzxORuUFmPzi2DzS3LnKpoVxR+TB+Ar23LnLSaWoUUFc5TYXN99KDMR5TxSPofpN2ywoR+PBZppZAQ62+YZnEwQURXasHGjFfsu3GBkRFjfHiNAqrABbD05G/YGURLD7I0X5e3tRG8NF83GjfY1TzB3JbR1lSKqUMz69DBH2bC66whdswnLpVUhmEdHrT5eWIC9+8SrYO7osCM7kfUUl0eFNrh6Cn8nNnTFdI6qWMoRijsWSovxin/PP1fRrCjpWZyHTw/lzltQLEOLC+Y8EdU7Hu3VhKpE1MaN1tM1MxMafi4lmCscHh4ezrdheMUR2iaPxMf/ViEOwOYxNQXj47ChK2YyWxU2uDwKRVRiPVWw+oNLHwraumcsE8FsTJk2AKxYUXb6q1bZag0LwfW9E9EebJdHFfcr2E7k/v2wuCisZ2/yqi4pOkcjIyBiWMuT0R7mqamq7iUoaOvusejv9cyM/Z6ksEFpUQof5iqaFaV6jIGrOnPnLbB8XBwtKZgHB+0Stc7DvGcPrF9xOFlEVfnw3rMnl0/JUIMU3q49e2B9fyBu4uJ/UwgQZ8OGnkNebdi4MWfD449Db9c8A8QI2ips2LAhl7YxtvOyYcVEtA3z89alXkU9TU/bcIxj9cQT3sSmSHFbb+g7kjwiUmVbP/ZYyIbug8nhN1V4gMM2rOubooOFeA9zBfHLkH+/zszYyXkblo977eCFO8JKC6OiWVH88NGQjHzn0ZZYPi6OlhTMIjYu9PHH7XNz3z44eXWMh3lx0T7QU3hnH37YHp/Mw97if10eztv18MNw8tqg/HF5VOl1DNtw0sqYIe4UNuzda3Xqww/DyRtmEIhuiyps6O62k8Eef9zmMzUFJw3EhGRUaYOLMd6zx9rQ1mbYyGPReVQRwwy2LcJtfdKaw1alz88XX5xCMOe19fIn49sBqsrjscdsx+Xhh+Gk4UAox7VFFSt9dHVZG377W5vPSf0lRH+V32uNY14CqGhWlHSEvzNveQI6K/tNbzZaUjADnHCCfWjv3m3PNw9NJK+bW2U85W9/a/NYtQpWdU97jf/duBEefdSKzd/9Dk7ZkCBAqlw5oasrZwPA5oESIRlV2GBMTqidvHEuP73CPCpM3+WRZ8OaEl7HCvPYtMm+PvKIzeOEE2AZc/F5iFTsPd240bbx+Lj1nJ6y/mh+mQvzqFII5tVT/wHvowlHj1pP/O7dcMrGwE0bJ8or/M6JFLf1KWv8j4iAbQtlCaCiWVGqI/xd+c+/hhXr61eWGtGygvmMM+D+++Ghh+z5KRuO2odo4RJXVT5YN2+2ccb33msf3ps3Y+NWPQ4Pn3661QK33WYnam3eOJufXmEeFabf1gZbtsB991kbenpg/cCUdxsA7rkn8DqeuJifXmEeFaYPtq1dOwCcMhwTzpDShnvvtffT5s1iGz8uJKO3t+JhqS1bbEzuHXfY883HBXG/nsRmb68V+q6t166FlX3i1cO8ZYt9/cUvrKd58wnB+m+HIyYvHjlSUZy34/TTczYAbB6KCbVK2db33Vdx0ZRmRUWzopSPWcz/jlz2G1h9av3KU0NaVjA/9al2o4zvftdql1OPn7ZiuTCessqh285OKxDuucf+nX56kEbc8HBXl10BogLOPNO+fvWr9vW0zcHwvKdwBpfHr35l/047DdpW9Hod4nY2XHedTfapTw2+aJ7CSlwejz8Ot95qF9g4cf2M187RypVWbN59t+2EnXYa8W1dpRA86yz7evXV9vW0k+dy6YVxqz9U0bE46yzbzvfcE4jbFSu8CmZnw9e+Zot52lOC+o/KI0U9Pfig7VisWgVDg4teRxOOO86uxfyrX1VctIZHRLpE5O0icouIfCXmGhGRD4vI7SJyl4hcWuty1gUVzYpSmpnD8NGQjvnzx2DVKfUrT41pWcHsHt47dliB07cmWKqs8OFdpScK4GlPg+98x3oGt27FPpzjhoerFIJgbejogLPPWsgvs6OKXfjCeTz2GNx4Y2BDnIiqUoD091ux+YVgLfNzzwu+bB7rybX15z8PZ58NnX09uQl+YaoU/WDr6eqrrbP0Gc8gXjCntGHHDvvxLacGbV1YT9NBx6/KPO69F37608AGz4L5+OOt2Nyxw54/47xAdETlcfhwVYL5zDNt037xi/Z+lZUlbKiwnkTs9/rOOysuWjMwDzwAfBiIU4SvBk4FzgcuAD4gIq0/1goqmhUliX13wSf6cud/OQ59x9evPHW/0VuqAAAgAElEQVSgZQXzeeflnpXPeQ65k0KRU6UQBHje83LH27aRLKKqEOQDA9YOsK89q3ty6YVxS2hVkcfzn587PlZPHoe4IVdPfX1w1jO689MrzKOK9J/97FwExLF2iMojRVuH6+mCC7DljAvJqDIO24U0XHABtPcHYrJQDFYpZgH+6I9yx895DqU7R1XEGLs8jjsOTj4jaOs4D/PKlRWlD3DhhbnjY209O1s8OTLl9/rnP4d//deKP9rQGGMWjDE3AhHLlhzjImCHsUwA1wAvrkkBGwEVzYpSzI8/BP90Tu788gXo6ou/vkVpWcG8bBm8//12W+O3vpWcN6tQRKXwOr785TZ+9k//NPAQxsUwVxlqAHDFFXY95ve+l0xsOOcca8c551g7SgrmKvJ461vtCgd/9VfQuXyZjWfxWE99fbatTzwR3vxm4uspheh/9autd/PP/gxOOgnvHmaA973Pbv7x7neTs8HjiMgFF9i/3/99eMELSBbMnZ32r0Le8Q4rlj/4wcD7C15DMtatg7e/HU45BV7/ekp3jqqoJ9fGO3dW/NGGQEQuFJGdEX/DZXx8ENgbOh8B1sbkc5mI7BKRXfvd7ketgIpmRclxpcCtH8ydX2FAWlY6JlL+vrRNyPvfb/8AeCx4sHoUICtX2iHuYyxfHr0eVQoR9bKX2T8AHvfvORWBa64JveFEvzH5E9cmJ6sWUWefndtN8Fg5PYvND33I/gHws5h6StGxWLOmIK41KYa5Shte+1r7B8B9MWLTTaCrwjvb3g433xx6I04wHz5cVfoAz3pWaKc8021nlhbmsbBg26IKwQzwyU/aPyC/c9Tfn7soRVsff7ydVNisy4kaY24Cbqry4/vIF8jDQOSaIcaYHcAOgK1bt7bW1l5XGLjhMvjlZ+35lWLXmG3xZbMUJY/CzmKL7uBXLkunm1DK61ilyMkjKYa5CkEemT54Ff2ReUTF/6YQs5F51LOefNjRGzM58ujRqoVgHnEe5hSCOTIPz4I5D5HoPJyY9VFPGbV1s4plD1wHvBFARHqBlwHX17VE9eKFO+A//SR3/vHlcPcX6lceRaklKpaLqFowlzPjOrjuwYJhwU3V5pmKWoioDDynRem79ArTD/8/qzx8iFmXR2H6Lg61FvXkS5R7jGEuIk4wu3Nfgnl2Fubm8t/3JZjBplO4rJw79ymYs2zrFkdEhkVkZ3D6deAJEdkF3Ax8xBgzUrfC1Zvjzof3hL4f179RQzSU1qZw2ThQsRyQxsNccsa1iHQA+4wx20J/j6bIs3riPMy+PXZxw/Q+0l+2zC6XkaUNcQKkypjTSKLqyacQTLLB5e8jjyw7R6U8zFmKTV/3K0R7mH22Q9z3+sgRuw1kR0tHnVWFMWanMWZ76HyvMWZbcGyMMe8yxmw1xjzDGPMvdStoo9DWoXHNytLg7i/kLxt37ttULIeoWjCXOeN6I9AtIteJyK0i8o5q80tNnIfZt9iMWv93YsKfAIkSar5FP0Tn0edpVmxUSMbEhH3N2oauLtvxSEtcWEmKGOY8lsVMjsyiraO+Ez47R1kK5rjvtc/vnKJAtGhejNi6XlGakSvFjqA43j4Kz/tU/crTgJQUzClnXLdhh/UuAZ4HvFBEXhCRR/azrZNE1LJlVkilJS7+16fYjPLOOhHlI49aCJAk0e/ThsI8fNrQ11ccapBiPexIosRmrQRzs3iY49ra53dOURxXGDh9e+78qk648S/qVx5F8UFUCEbP6vqUpYEpKZiNMTcVhFS4v71lfHa3MeY9xphpY8wM8C3gvIjrdgRDgFuHhoaqs6QUtRKCkP/wNsavAMnaO1sLARIlmLOwIUoI+rKhr8/uGhmO/02xqUgkUW2tgrk4fci2c6QoYV76Ffivoc7yL/5BQzSU5uS339d45QrIdJUMEdkiIm8JjtuA5wP12UOro8N6kaOEoE9xAPl5uBCNLMVmLWKYfQqQWnnJs/YwQ76X2acNEO9hbm+38bk+0odoQVsLwZx150gFs5IVy1ZEh2jMjNenPIpSKVcKXB3azeqlV6tYLoF3wVww4/oR4OkicgfwI+AOY8y3fedZNnFi06fAcWmG0we/Qs15Y8N5iPjxbLpyRq1s4LOe4lZO8FFPPT1WVGZpg0sn3Bbj4/n/S0ucYF6xws+6Z1GC2Y2IZBnD7HPiYpKXXEMylKy5wsDwubnzTwyot1lpbBZmo73Kp7+yPuVpIlJPITfG7AR2hs73AtuC4xngsrR5eCNKqPn0OrqNE8ZDXgYnqHwKtUcLFhpxNvgQUVE2hPPwgRP94c1RfNaTiE0nyoZ169KnD9GC2R2HN9BIQ5zY9D0iEs5jZsbG4TdLSEZvr+0cFXYiJybgKU9Jn76ilOJ1u2BhDj4Wmkx8pcDli0t6QW+lAYnqzKlXuWyWzsYlEO+d9SVmo8Smbw9zf3+xEMzahpkZG6vrM4+FhXxvf7PWU5RgztrDnKVg9t0OrpMaXjnGp2CO6xyph1mpJe2dxcLjo23qbVYag8WF4nvxHQdVLFfI0hLMAwMwNpb/XrN5mKOEoO+Ji21t0Tb4rqcosZmlYM4ihjkqJKPZPMxZhhCtXAmLi3ZCpOPIEbtkno/l/SD7tlaUcrnCwJsfzn/vSoH5mfqUR1GuFLiqIJjgCgPdq+pTniZmaQnmOK9jloI5C8+pC2cI5+Er/SiPXRY2QHEePT3+NprI2sOcFJLhK4+VK7O9X6MEs88JeeE8wsLft5gtbOv5ebuCiXqYlXowcFKx5+7vu9XbrNSW0QeL77k/f1S9yilQwZx1OEMWHuaocAaf4qCwnrKwAYoFc5Y2uDrL0sPsu55WrSq+X32uYNHRYdM6dCj3ns8JeZAra9iOsTFrmy8K29p3B09RquEKYzd/CHOlwK++WJ/yKEuHKwU+tyX/vSsM9G2sT3lahKUlmAtDMhYX/S+h1daWL6Jq4Z3NwmPXCjaE0/ftOa3FKhkDAzZ+PBzO4HMFC5dH+Dvhu62dMA7nMTbmL2wFVDArjUvP6mKP3ndebwWNWaxLkZQW5kop9ipfvqBeZU8sLcHsHqwunMG3iEoKZ8hyspnvNWfr5WFuJhuWL7ftXehh7urys2skWDEL+R5g32KzUDC7Y5e3j/TD6YJtF1/pQ/ZtrShpucJETAps1zANxQ/3faX4Xjr3bfaek6Ul87LEU8Bok9Dfn4tv7O3NxhMV9fD2tdGESx+y987u2ZM7b0YPs+u4uKXrfNvgOkeFgtmnSAuLzfXr7YjI+LjfcIZCwezEua88XDqFov+00/ykD+phVpqHKwwcuA8+/9Tce07oqBdQqZSpg/CpweL39V7KhKXV9Sj0dvkWB1DsYR4ftw90X+txForNLERUoQDxvfpDlGDOIq51YQEmJ/Pz8umdLRTMrq19URjO4CZ7ZimY3bGvPGrhJS8cOcqirRXFF2vOsILmpBfmv3+lwJefVZ8yKc2FWbT3S6FYjhrJULyxtARzoVBzD/HVq/3mERaCBw/6Tx9yeRw+bEVzloL54EH76ssOt1NdOI9Dh/zbALk8fNsAxZ2jLD3MkE0HL8rD3NXlb0QkKoY5i5CMcOcoi7ZWFN+88vpicbPnx1YIfft19SmT0tgYY++Pj7bnv//WfSqUa8DSFMzu4e0erFmLzSwFc5ZC0HnsDh60Aqqnx0/6bW3FYrOZ68kxPt4agtln+r29djUOV/b5eTt3wLdghmzbWlGyIsoreM8/W2H0by+qT5mUxsJ5lD9aINku+Z69d5avrU+5lhhLSzC7h3SWD9ZWEMzhWG+wYse3+BgYyNkwM2OXfGu2elq1Kl9s+m7rQsHse0KeS2t83I5SuDx8CmaR/Hpy7ZGFYM6yY6EoWRMlnB+5IXrlA2VpMDUa7VF+4WftvXLi8+pTriXK0pv0B7UPyTjlFH/pu6XrCoVgVuEMvb3+haDLo7AdsgzJcHn4jGtdswbuvTd3Pjpq3/NFYfxvVh5mY2xoT3+/fw+zy8OVPYv44qjO0cqVdjdBRWk2nGguFMk6OXDpcPcX4Po3Fr9/8VfgjO21L48CLFXBHA7JaG/3O4w+OGjFweKiFba+vbMiVoCMBgviZyH6B4OJBKOjdnWGLATz6tU5sZ+1DWDzGhiw7e2LNWvgwAF7bIzNazBixnK1dHfbv6xDMiA3Ee/QIdvmPgl7mN1rFpMjXf1kcb8qSq0pJZzfuk+H4luNuJGEN9wNQ2fVtixKEUtLMBeKqEOHrGDwtYIFwNCQFcvuoZ1FOMPatbB/vz3OItRgbfAj/OSTuTw2b/aXPth6uvvuXPrg14ahIfsariff7TA0ZENJpqZgdtaGsfgUzJAfY5yFYA5PyjvhBPt6+un+0nd5uLK7DoZrHx+4+zXLtlaUeuGE8+fOgNH7c+9/Zp197TsB/vy3NS+W4omZCfhEjAPhPXPQtrRkWiOztFqiu9t6k/fts+dZPFjDYrO93XoeayGYfYqoQrFZK9HvWwi2t+eLft82uPCLAwdgbs4e+xbMq1ble+Lb2/3u9Ofq3AnZLOppYAAeftgeu/bIQjC7tLO4XxWl3rzpPvs68nP45/Ny70/8LueZfMsIrBiufdmUykmKS9ewm4ZkaQlmsA/XsIjyHa8ZFptux7cs8rgv+PE8eNCuXuFrGTCI9jD7tmHtWpvu3Fw2grmtzQrasCj3bUNYMM/P22PfgnndulwH78knbb35HBEZDh6u+/bZyZdjY7n290U4dMXdUz7zWL7c3v/h+/WpT03+jKI0K+ufER+u8b9D4VQquhqP2z8GO98T/b8X/xOcpcsJNjJLTzCvW5d7sO7bZ4ehfRIWm27SkW8BsnYt7Nxpj/ftszb5ZPVqK8r277dLgE1O+rfBdSwOHMgJQt92DA3lBPO+fX4nX0K+YF5YsMe+BfPwMOzaZY/37s0JXJ/pu7Td98J3OwwPW6/v9LRtj85OvzHMIvkd4X374LnP9Ze+ojQqThQ/9C34+kvz/xcW0yqe68fub8M1F8X/X9umaVh6gnntWvj1r+3xyAj8h//gN/2wh7ktWLXP9ySqoSHrRZuftzb4FlHt7Tnv7MiIfc+3DeG40717rZfQ91bGTkQZY+3wbUOUh9nnKhlgxevevfY4i85Rf78dCdm7N9dx8X0/uXp3onxoyK+XHHJtPTNjvxu+21pRGplTLo73Ohe+d/mi/++fks9tfws/+m/x/9cJm03J0hTMP/qRFTj79/t/sDoP4/79ubVtsxCbblWGvXvhKU/xmz5YUfPkk9kJZtexcHlkIXCGhuDOO22YwcyMfyHoxPH+/bld5o47zm8ew8PWy3/0qBW0Z57pN30Rm8e+fdl5+gsFs+/RCrBp7t2b61yoYFaWKmGPZZR4Dm9+8aofwqZtmRdpSVBqreztN8EJOvLVzCxNwXzggBVpxvgXUZ2dNqRh3z4bn+tiaX1SKDYvuMBv+pDz2DnB7LuewqErWYQauDyyFP2rV1vv7OOP25Uy+vutp9wn4ZCJLDzMkPNiO7GZRUgG2HbYuzcbG9autauuZHW/KkozUko8f6VAwL1rCjo8zodpZa67BB74t+RrXvtzWL+1NuVRMmfpCeYNG6xQvvNOe57Fg3XjRvjd76xXc906v2v/Ahx/vH196CE7/JyVDTt3Zic2nSf20UdtHk97mt/0ATZtsptZPPCAPfdtQ1ubjYH/7W/tiIVv7zLkxOW999ql67LwnA4PwyOPwBNP5OfpC1fmkRH7vfi93/ObPtjv9cgIPPZYfp6KoljC4vnWv4Yf/4/ia/6+J//8st/AKs9zP5qVj3XDwkzp6zTkpWVZeoLZrSf8ve/Z1xNPzCaPe++1XsdNm7JJH+AHP7CvWdnw5S/Dgw/a3f58L9O1cqX1Cv7mN1ZEXZQwKaJaTj7Zvt50k33Noi1OOMGW35hsBLOblPr979tXZ5NPNm2ynaPdu60NPldcAdvOHR2247J/v/+JtmDv14UFuOUWe55FWytKq/AH/93+gf3tCodphNlxavF775yEzp7i91uJH14OP7uqvGtfejWc/spsy6M0BEtPMLuVEm64wb763pDDpfnv/263G77wQv/pr11rh/6dDb5XfwArzIyxHYtTT82mx7x5M9x8s1094dSIH+a0OHF5ww02VCYLoXbiiXDttdb7++pX+09/82Y7QvHtb9vzLATzli0wMQG33ZbN96G93bbvd79rz7Pq4IFt61Wr/K9Woiitiki+9zlJQAN8vDcijTZ49yy0eR5NzZoHroHr/mNln7n4X+CMDH7rlYYnlWAWkb8Dngt0At80xvxtwf+XAf8AnA50A5cbY76fJs/UbNxoxdPu3XYo2vfKDGAf3rOzdog7CyEoYkXyL39pz7PIw4nw3bvhP1b4g1JJHj/5iT3OYuKiE1G7d8Npp1kvp29OOSW3dN0ZZ/hPv6vLiuTf/MaGgJx0kv88tmyxrw89BM95jv/0we4e+I1v5OfnE3e/PvQQnHeeDokqSrUUCmiAh2+Ar70o/jNmEa5K+H1dsQHeeC90D/gpY7nc8Rn4/tvSpaEhFkpA1QpCRF4CDBtjniki7cBtInKdMebu0GXvAcaCa44DdorImcaYMgKBMqKjA849F376U/9LyjnOPz93nGUev/ylHUL3uWua4+yzc8fnnRd/XRrOPx++9CV7fO65/tNfudIKtfvvz64dnvnM3HEWsbkA55xjBfNTn2rDY3wTjh9/xjP8pw/2fnKC2fdKH2BjmIeH7aTCrO5XRVmqnPzCYhE9P10c8xzHkSfgk543jvLNH34Ctr6j3qVQGpiEcZdkjDHfBv6iIK3pgssuAv4xuH4P8BPg2YVpichlIrJLRHbtd966LLn0Uvv6qldlk/5ZZ1lxc9xx8Ad/kE0e27fbXu/rMtoZqKcHLrnExrP+yZ9kk8fFF1sBePHFdsvyLHBtvX17Numfd571+p5ySnZC7TWvsa/OFt8MDcFLXpJriyzYvt16yy+9FJYt85++CLz2tdYLf8kl/tNXFCWfjm4roqP+3rqv3qWL5vc/EF9mFctKCcSY5F1mRORCIGoF7u3GmL2B53gH8P+MMZ8r+Oyvga3GmIng/ErgLmPMV+Ly27p1q9nldjbLCmNgz57cahNZcPiwnYQ0kOEQ1J49djWAtqr7PcnMzma3CofjySdzm2dkgTF22beNG7NJH+xKHCLZiX6wbb1hQ3ZDgzMzNo45i9EKx759dvKo2wHTN4uLdqWMLCZfVoCI3GGMWVJrSdXkd1tpXcZ/B7s+Cb/8R5ibLO8zq0+DZ/4VnL4d2pbedCzFH+X+Zpe8y4wxNwE3xWSyDXg38E5jzIMRl+wD1gITwflw8F59EclWLEM2sdGFZC0Mli3Lfj3bLDaxCCOSrVgGv9s8x5F1W3d1ZSuWIZv1l8O0tdVdLCuKUgX9J8Afftz+KUqDUrVrUkS2AO8EXhYjlgGuA94UXL8OOB+4rdo8FUVRFEVRFKXWpBnHeBOwGbhRcsPEHwceBd5rjNkOfAr4vIjcDgjwlrpO+FMURVEURVGUCqlaMBtj3o0Nx4hie3DNLPCaavNQFEVR/CAiXcCbgVcAe4wxkbOeReRBYCT01muNMY/WoIiKoigNi0bKK4qiLA3mgQeADwORy+uISAewzxizrYblUhRFaXgyWl5BURRFaSSMMQvGmBuBqYTLNgLdInKdiNwqIrrWlqIoCuphVhRFaSlKLQVa4uNtwM3ABwEDXCsiDxhjvhuRz2XAZQCbNm1KV2hFUZQGRwWzoihKC5G0FGgZn92N3aEVABH5FnAeUCSYjTE7sGvws3Xr1uQF/RVFUZocDclQFEVRALtcqIi8JThuA54P3FnfUimKotQfFcyKoihLGBEZFpGdwekjwNNF5A7gR8Adxphv161wiqIoDYKGZCiKoiwhjDE7gZ2h873AtuB4hiAuWVEURckhxjRW6JmI7Ad+V8VH1wAHPBenkWhl+9S25qWV7avWthOMMRnvM95YVPm73Uj3jpalmEYpBzROWRqlHKBliSLT3+yGE8zVIiK7jDFb612OrGhl+9S25qWV7Wtl2xqBRqpfLUvjlgMapyyNUg7QstSjHBrDrCiKoiiKoigJqGBWFEVRFEVRlARaSTDvqHcBMqaV7VPbmpdWtq+VbWsEGql+tSzFNEo5oHHK0ijlAC1LFJmWo2VimBVFURRFURQlC1rJw6woiqIoiqIo3mkJwSwirxSRn4nIHSLy9/UuT1oCe34iIreKyL+JSK+IPF1EbhaRn4rIt0RkVb3LmQYR+aDbLKGVbBORjSLyTRH5oYh8T0R+T0Q2icgNIvJjEdkpIifUu5zVICLvD75nt4nI10RkZTO3nYi8Ivh+PRp6L7KtRGSZiHw+eP9OEXle/UrevIjI3wV1+HMR+WDE/2tSzyLSJSJvF5FbROQrCdc9GNwH7m9Trcshlg+LyO0icpeIXOqzDJXkIyIdInKgoE6WeSxD4rM8qKufB+V7t698qyjHzoK/8zIqR9FvVCXlrHFZvhg8B1ydvDTDshRppIL/Z3OfGGOa+g84AXgQ6AcEuBp4eb3LlcKe1cAuoCc4vwp4B3A/8PTgvb8APl3vsqawcSvwBezmCdJitl0PPC3UlkPA94CLg/deDHyr3uWswq6zgNuB9uD8fwHvaea2A56DXbdzb+i9yLYCPgD8fXB8HPAboKveNjTTH/AS4PPBcTvwU/ddCV1Tk3oO8n8+8CLgqzHXdAC3ZFwn5ZTjUuCa4LeyD7gPWJ9BWUrmA5wE/GtGdZH4LAeeBfwEWBb8/QjYWutyBNf8JMv7IpRP0W9UJeWsVVmC/99EoFsyrpMojfT2WtwnreBhfiHwdWPMuLG19Y/An9S5TFVjjDkIPNsYMxW81QFMA4eMMb8M3vsc9uHTdIhID/AJ4L3BW0+hdWwbBrqBN4jILcDfAUeBLcaYbwEYY74DnOnTK1MjDgAz5HYHbQcmaOK2M8bcbIw5tsh94KWIa6uLsL8tGGP2YH+Qn137Ujcvxm6x/Reht9qwv21halLPxpgFY8yNwFTCZRuBbhG5LvBkvaNO5bgI2GEsE1hR+2LfZSkznxOBtSJyfVAn2z3mX+pZfhHwf40xs8aYWazT5Y895l9WOUSkA+gPPJu3iMjfikh7BuUo+o2qpJw1LgvAAPAPQZ18ptDr67EcURop/P3J7D5pBcE8COwNnY8Aa+tUFi8YY6ZFpFtEPgn0APcQsjG4CZp1W/OrgE8YY54MzvPar8lt2wScA3zRGHMB8AS2c7C/4LonsXY3DcaYEeAzwP8RkfcBh2it+xLsD35cW7Xc70xWiMiFEUPWO0Vk2BgzIyLHAd/EirNfF3zcaz0nlaWMj7cBNwOXAM8DXigiL6hDOWpSJ2XmM4kdGbwo+HuPiJxRbVkKKJV/rb6DpfJZgb0vLsNuKb8eeFMG5ShFo/0m7QI+GDz79gNFIVe+iNBIXwj9O7N6aeaHm2MfdpjIMRy817SIyPHAZ4FPGWOuF5HNhBpcRLqA2XqVr1qCh80qY8w1obf30QK2BYwB9xljfhGcXwP8H4rF8RCNsY1o2YjIc4ELjDFvDM5fCfwXWqftwLZJXFu5+3QieL/pf2eywhhzE3Z4tggR2Qa8G3inMebBiEu81nNSWcr47G5s2BEAIvIt4Dzgu7UsBwW/kdg6qXQb8pJlEZEvlcrHGHM7NjQLYFxEfgCciw3fSEupZ3lUPWTxHUwshzFmDPhzdy4i3wBeTjAyUkMaSvsYYy4LnX4N+HRWeRVqpIJ/Z3aftIKH+TvAn4rIyuD8DcB1dSxPKkSkG/gn4DJ3IwQ/3CtE5MzgstdgY2WbjYuAIRG5VkSuBc4E/prWsA3gIewQ7pbg/HnAHcCvROSFAGInMd1rjJmrUxmrZQvQFTpfhu1wt0rbOQ95XFtdR+BFEpF1wPnAbfUqazMSfC/eCbwsRixDA9WziGwRkbcEx23YWOM761CU6wDXUe0FXkY237OS+YjIs1wYRtBB3gb8Aj+UepZfB7xWRDqDEIjXYUcqfJNYDhEZFjsBWoK3Xkh97ouG0T4i0hOEprhQwxeRUZ1EaaQCMrtPmt7DbIwZEZH/CdwiIrPArcaYr9e7XCl4HnA68KXc95GbgNcDnxWRRWAUexM0FcaYt4XPRWSnMea1InI2TW4bgDFmUURej43j6sAO578BO9T/T2JXBZgB/qx+payafwbOF5F7gHFszNibsLY1fduFeAvRbfUp4PMicjt2gs1bjDEzdSpjs/ImYDNwY+i37ePAo8B7jTHbqXM9ByESXzXGbAMeAZ4uIndg74XrgzjsWpfj68Dvi8guwAAfCUKkfBOZT/D77NrnfuAdIvIuYB4bVnOPj8zjnuVBuMh2Y8wuEfkm1sO9gK2fXT7yrqQcWG/lCuBOETkC3EUNN+4Qka9i2+auemufgrIcAH4mIuPAHuDNGWUbp5EuJOP7RDcuURRFURRFUZQEWiEkQ1EURVEURVEyQwWzoiiKoiiKoiSggllRFEVRFEVRElDBrCiKoiiKoigJqGBWFEVRFEVRlARUMCuKoiiKoihKAiqYFUVRFEVRFCUBFczKkkFEjheRS+pdDkVRFEVRmgsVzMpS4g+B36t3IRRFUZTSBFsu3xxscZzn9BCRZSJyS7CrqqJkjgpmZUkgIs/GbsP7ChG5S0ROqneZFEVRlETeAHzDGLMQnB9zehhjZoEfADpqqNQEFczKksAY8yPg58AfG2PONsY8Uu8yKYqiKCAiPxSRPwqOPyQinwr+dSlwXfB+lNPj2uAaRckcMcbUuwyKUhNE5BHgKcaYuXqXRVEURbGIyAXA/wA+C7waeCnQDjxqjBkOXXcD8G5jzD3BeTuw1xgzVPtSK0sN9TArSwIRGQTGVSwriqI0FsaYWwAB3glsD0Iw1gBjBZeeBjwY+twCMCsiK2tVVmXpooJZWSqcBDxR70IoiqIo+YjIWcB6YD5zNBEAAAETSURBVMYYczh4ewroDl0T5/ToAqZrUlBlSaOCWVkqPACsEZF7ROSZ9S6MoiiKAiKyHvgX4I+BoyLyAgBjzCGgXUScaC5yegQier+OHCq1QAWzsiQwxhwxxpxnjDnTGPPjepdHURRlqSMivcA3gHcZY+4H/hb4m9AlNwLPDo6jnB7PBb5To+IqSxyd9KcoiqIoSsMhIucA7zTGvCbm/98A3meMeTDq/4riE/UwK4qiKIrScBhjfgH80G1cEkZElgHXqlhWaoV6mBVFURRFURQlAfUwK4qiKIqiKEoCKpgVRVEURVEUJQEVzIqiKIqiKIqSgApmRVEURVEURUlABbOiKIqiKIqiJKCCWVEURVEURVES+P+QG2nf4ZFnqgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"def heun_2var(x, func,t, dt) :\n",
" temp1 = np.zeros(2)\n",
" temp2 = np.zeros(2)\n",
" temp1 = func(x,t)\n",
" temp2 = func([x[0]+temp1[0]*dt, x[1]+temp1[1]*dt], t)\n",
" val1 = x[0] + dt/2.0 * (temp1[0] + temp2[0])\n",
" val2 = x[1] + dt/2.0 * (temp1[1] + temp2[1])\n",
" return val1, val2\n",
"\n",
"if __name__ == \"__main__\" :\n",
" dt = 0.01\n",
" n_step = 10000\n",
" calc_plot2var(heun_2var, harmonic_eq, dt, n_step)\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Runge-Kutta method and further: Using \"scipy\", scientific library of python\n",
"\n",
"The accuracy of the previous method is \n",
"$\n",
"O(h^2).\n",
"$\n",
"Usually the forth-order Runge-Kutta method is used:\n",
"\n",
"$$\n",
" x(t+h) = x(t) + \\frac{1}{6} (k_1 + 2k_2 + 2k_3 + k_4)\n",
"$$\n",
"\n",
"where\n",
"$$\n",
" \\begin{eqnarray*}\n",
"k_1 &= & hf(t, x(t))\\\\\n",
"k_2 &= & hf(t+\\frac{h}{2}, x(t)+\\frac{k_1}{2})\\\\\n",
"k_3 &= & hf(t+\\frac{h}{2}, x(t)+\\frac{k_2}{2})\\\\\n",
"k_4 &= & hf(t+h, x(t)+k_3)\n",
"\\end{eqnarray*}\n",
"$$\n",
"\n",
"Imporved methods derived from Runge-Kutta are implemented in \"scipy\" where the most appropriate method is automatically selected (probably). These are implemented by C libraries such as BLAS and so it is very fast. The standard library is \"odeint\"."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAswAAAFCCAYAAADlg4svAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzsnXl8XWW1938rc9KkSZqkTeeBsVCk2CIylTIpIjIqqFxRUbmC4ovIcOEq6sVXZVTRqy94LygyiFC5TCpXhrYUhNJChUIp0IkmTdI0Q5O0mfO8f6yze3ZOzrCfZ4/nZH0/n3zOyTn77P2s7LOzf/u317MWKaUgCIIgCIIgCEJy8sIegCAIgiAIgiBEGRHMgiAIgiAIgpAGEcyCIAiCIAiCkAYRzIIgCIIgCIKQBhHMgiAIgiAIgpAGEcyCIAiCIAiCkAYRzIIgCIIgCIKQBhHMgiAIgiAIgpAGEcyCIAiCIAiCkIaCsAeQSG1trZozZ07YwxAEQTBi7dq1u5RSdWGPI0jk/7YgCNmK0//ZkRPMc+bMwZo1a8IehiAIghFEtC3sMQSN/N8WBCFbcfo/W1IyBEEQxglE9Gki+hMRfZDi/d8T0ctEtDz2c2bQYxQEQYgikXOYBUEQBN9oBXAZgPUp3p8J4ESlVG9wQxIEQYg+4jALgiCME5RSK5RSu9IsUgXgN0S0koh+RURlQY1NEAQhymSFwzw4OIiGhgb09fWFPRRPKSkpwYwZM1BYWBj2UARBEABgDYAblVLbiej7AL4H4LpkCxLRJQAuAYBZs2YFN0JBEIQQyArB3NDQgIqKCsyZMwdEFPZwPEEphba2NjQ0NGDu3LlhD0cQBAFKqUtsvz4M4Jdplr0LwF0AsHjxYuXz0ARBEEIlK1Iy+vr6UFNTkzNiGQCICDU1NTnnmguCkJ0QUSkR3UhERbGXPgHgtTDHJAiCEBWyQjADyCmxbJGLMQmCkF0Q0R+JaGFsot8uAKuJaAWARQD+I9zRCYIgRIOsSMkQBEEQvEMpVW97/lnb818A+EUogxIEQYgwrh1mIjqfiP5BRC/E6nuWJbz/LSJ6lYjWEdFVbrcnCIIgCIIgCEHiymEmokkArgFwvFKql4huAfBVAHfE3j8WwOcAHBv7yHNEtFwp5W1LqJ4eYHAQqKoCsjXNoaEBePll4FOfAoqLwx6NGbt3A08/DZx8MlBTE/ZozBgcBJ54AjjiCCBbJ2MqBTz7LO+DI44IezTmrFnD36mTTsre41oQhLEoBex6C3jnYeDdZfzclPLpwIzjgDmnAgecBZTVejdOQbDhSjArpdqJ6DillDVzrQCAveD9GQDuUUoNAAAR3Q3gLHDpon24Lk/U2gq0tQHTpvFPwPT29uK0007Dc889h/z8fDQ0NODFF1/EBRdcgIGBAZxyyil47rnnUFCQ4s/d1gYsWgTs3Amcey6wbFmwAXjB8DBw6qnAq68ChxwCvPZadgr/f/1X4J57+OLrjTeAmTPDHpE+d9wBXHEFkJcHPP88sGRJ2CPS59ln+fukFPCb3wBf/3rYIxIEwQnvPwk8fgEwuDeY7fU0Au88xD9/+2rm5Rd9Czj+RqB4ov9jE3IK1znMSqk+IioBcBOAYgB3296uAfAP2+9NAI5Ksg535YnmzAFGRoDmZmDyZCCVMPWJu+++G+eeey7y8/MBAM8++yzefvttXHDBBSgqKsLJJ5+Mhx56CBdeeGHyFdx2G7BrF/CZzwAPP8yi88gjA4zAAx55hMf9uc8BDz4I3Hsv8LWvhT0qPTZsYLF83nnA448Dt9zC4jOb2LsX+P73gWOPBbZuBW64AVi+POxR6XPddXxc19VxPF/+cnZegAlCLjLQAyw7E/jgee/XXVwFTDoAmDgbKKnmi+ahvcDgHt5uXzvQsQkY6DJb/9o7+CcZ5zwKHHi2+diFnMa1siSiGQB+C+AOpdRfE95uATDZ9nt97DVzrrgCWLdu7OvDwywWSkoA3UYgCxcCP/95xsVOPPFEXH/99Tj11FPx3e9+F11dXbjjjjtw//3344EHHgAArFq1CldeeSWqqqrw9NNP49FHH8XZZ5+N6667LrlgVgq47z7g4x8H/uu/gCefBP7wh+wTzPfdx27sffcB//wncP/92SeY77sPyM8H/vM/gaIijuH22wO/AHPFk09yGsONNwKrVwP/9m8snOfMCXtkztmwgS++fvYz4KCDgNNPB/72N+Css8IemSCMP7o+AH4z2+yzJ/wE+PDlQNEEb8eky843gL9/A2hYlX65R88Z+9rSm4CPXC1pYYLrHOYSAL8D8GWl1PYkizwG4HYi+j2AEQBfBODPxL/8fL4FPTSkL5gd8sMf/hA33HADdu7ciddffx2PP/44BgYGsHnzZsyJCZLjjjsORx55JG699VYsWLAAADA8PIxXX301+UoHB4Ht21ngTJzIt6Efewz4xS+y5wDt7eXc5csv533w6U8DP/oRp5pkUy7z448DS5cCU6ZwasyDDwIvvgiccELYI3PO//wPj3/JEmDGDBbMTzzB+yZbeOopfjz/fKC2Fqio4NdEMAuC/7xyM7D8WufLf+FlYNqYG8fRYvKHgAtfSP7eQA/wly8DGx9J/v7ya0f/PfKLgMtbJaVjHOLWOjsFwHwAf7DVFH4OwEkAPquUWkNEjwN4BcAwgD+6nvCXzgneuhXo6GDH2AexuWTJEiilcPvtt2P58uXIz89HS0sLqqqqRi23ceNGHHTQQft+z8/PR1FREbq7u1FRUTF6pVbjkpNO4sfTTmPhtnVr9kw6e+UVFv5WDKeeCvzHf7DYPPPMcMfmlLY2YP16TikBOAYiYMWK7BHMSgEvvMDjzc8HDjgAmDePUzKySTCvWAEceGB8PsLJJwPPPBPumAQhV9nwEPD4ZzMvt/DrwMf+E6Csad/gjKJy4OyHx77e8CJw/3FjXx8eAH5eOfq1K/cChaX+jE+IDG4n/T0JYHqSt/7DtsytAG51sx3HVFRwLnBvL1BWlnl5Td588000NTWhtrZ2n/AtLS0d1a2vra0NlZWVKExwufv7+1FSUjJ2pf39fLvcmlx2zDH8+I9/ZI9gfuEFFpfW2Bcv5pSGVauyRzC/+CI/Hn88P1ZWAgsWAC+9FN6YdPngA662YsUA8D555hkW09lwx2J4mL9P558ff+2YY9g5b23lnGZBEMwZ2AP8rDzzcpduAyYaTMLPFWYcC1ybMKXq+WuA1beMXfZ2m974+F3AwixLRxQckVuXihNieVJ79ni+6qamJlx44YV47LHHMGHCBDz99NMAgOrqagwPD+8TzVu2bMG0hEodbW1tqKurGyOiAbBgPs52FbtgAVBenl1C7aWXgEMPBaqr+feSEhbN//hH+s9FiZdeYpFvzx0/+mgu9TcyEt64dLC+M/bv09FH82TYbdvCGZMuGzdyDvaxx8ZfOyp2u3f16nDGJAjZTsvrwE3EP6nE8jeaWCBaP+NZLKfixJtH/42W3jR2macvif+tHzkj+DEKvpFbgrm4mHNoe3szL6vB3r17ce655+K2227D/Pnz8b3vfQ8/+MEP9r3/sY99DKtW8WSCgw8+GLt27cKCBQvwUkzAPP/88zj99NPHrnhoiB21hQvjr+Xnc+3cZBMbo8obbwAf/vDo1xYu5NeVftGTUHjjDWD+fBb7FosXs3jLFrH5xhucv3/oofHXrAuA118PZ0y6vPkmPx5+ePy1RYv4uBbBLAjOaV0fF26/+/DY989eNlr8ldePXUZIz1HXxP9+VyYx6jY9Fd8H934k+PEJnpJF0/8dQASUlnK1DA8pKyvDP2xu6ZIlS0b9/s1vfhO33347TjnlFJSXl2N1won9gQcewE9+8pOxK7aEfWxy4D4WLAAeeCA7bqO3twM7doyN4bDDgK4uThOYbTjDOkjWrx9br9iKaf367EiPefNN4OCDR096PeQQfnzrLeCcJDPAo8Ybb/BF4/z58dcmTAD2359jEAQhNb1twB1pGndc1ghUBN+rYFxQWDY6hePpS4F1/y/+e9OrLJwB4PgfAcf8e7DjE1yTWw4zwLnLvb2BOptHHHEETjzxRAwPD495b2BgAGefffaoSYD7sIT9YYeNfn3BAnY2Gxt9GK3HWCImUTB/6EP8aDmGUaazkyuVJO4Hy6nNhhgAFvaJ+2HCBBb769eHMyZd3nyTS8kl1lw+5BDg7bfDGZMgRJ37j2cxlkwsX9EZd0FFLAfHx38T/7sf98PR773w3bjz3PZOOOMTtMk9wVxaymkOg4OBbvbiiy/e17jETlFRES666KLkH+rr41vNU6eOft3ubEYda4zJXHIgO8RmKtE/cSIwa1Z27IeuLk4dSYwB4NeyIQaAvy+JFy4AC+b33gMGBoIfkyBEEXvKRWJ94X/dHBdrxZXJPy8Ex7E3xPfHzISqS/81n/fhfccm/6wQGXJPMFs5qP394Y7DCb29fPs8Me3Ccjaz4Rb0+vUsLGfMGP36xIlcFuzdd8MZlw6pBDPA+yIbnE1rjPb8ZYtDD+XJdAFfRGqzdy+XU0wWw/z5nPP//vuBD0sQIsVTX2KBdXfCheVS24S0qixIIRuvfH55LOc5IXW08aX4BdDeXaEMTUhPbuUwA/FbuX19XGYuyvT3J2+yUlMDVFUBmzYFPyZd3n+fa+Ymy7Xef//sEDibNnGFDKu0n5399+cyZ1HPJ7f+zslSfw44gMXm9u1clzmqbNnCj/vvP/Y9Kxd7w4b4c0EYLygF3JzC37pqAMj3p1mX4COFpfGc5zV3AM/+n/h7v4yVzzzvcWD/TwU/NiEpuecwFxWxsIm6w2yljaRqu7zfftkhmLdsSS3CsiWGzZs5zzcvyeGw335ATw/XAI4ymzfzY7IW2Pvtx49R3xfW+JJ9nywRnQ0XYILgFf3d7DgmiuWPXB13k0UsZz+Lv8X78orO0a8vO5P3/4rrwhmXMIrcE8xE7DLbmolEEisXM5sF8/Aw30JPJZj33x9oavKlLranbN6cXvQD0d8XW7ZwCkyy5jhWbFGPwRL91t/czsSJwKRJcRdaEHKZva0slH6e0H75i2tZWJ14czjjEvyluDJ+IVQ4If76yz/l78MfTw1vbEIOCmaABXPUHWZrfOkE87ZtfCs9qjQ2skueTjAD2SHUsl0wp4th+nQ+JrIhhooKTklKxty5IpiF3Ka7kYXRLyePfv3bPSyi6pPUUxZykytj+/zQL8Rf2/YMfz+WnRXeuMYxuSmYS0pYkEa5aYYTwWzlnUYVyxHMZrHZ0cFl5VLFMHcu37WIcgxAesGcl8dxWPsrqmzaxDGkyhUXwSzkKgM9LIR+nTB5+qoBFk1FE5J/Tsh9zriXvwMn3R5/7f3H+fvyl6+EN65xSG4K5qIibmccZXe2v5+FTJJSdACyQ2xmEszW61EWapliKClhhzbK+6Gvj93+dBP6siHFZ/Pm5OkYFnPn8l2XbGlVLgiZUCrWrjphgvo1w5KfLIzmyG/zd2LJj+OvvXk3f3/W/Ta8cY0jclcwA4GU0ert7cUJJ5ywr2lJQ0MDHnroIQDctGTJkiUYSibc+/vHNmewY03einJb5s2bWfAnqy4BcKWPCROy2yUHeF988EEgwzFi2zY+8abrRmiJzagyMpJ+AinAMQwMcGdJQch2kk3mu6qfRRHl5qlZ8ICjr+PvyEeujr/29CX8feqIuCmS5eTmUWkJ5gCaHNx9990499xz9zUtefbZZ/Haa6/FhlGEk08+eZ+AHsXAQHrBPG0a35puaPBj2N6wZQs39kiVVkLEYjrKgtm6xZ9ObM6YEf39AGSOobOTK35EkZYWvohMVuXDwopP0jKEbOaVW+Itki2+sSPmKBeFMyYh+zgxVnd7yhHx1+7an79bSu7C+UHW1WG+4gpg3boMC6lSoOcgoKQYcHBHa+FC4Oc/T7/M2rVrcdVVV+H5558HAKxfvx5f+9rXQER44IEHAACrVq3ClVdeiaqqKjz99NN49NFHcfbZZ+O6667DhRdeOHqFAwM8wSmVC15UBEyZEm2xuX17anfZYubMaIvNhgauwJCuZvfMmcCjj0a3FrP1HZk1K/UyVmOZhgbg4IP9H5MuVhv4xAY4diwxHWW3XxBS0dME/GdCa+oLngHmnBzOeITc4Ets0I26CLs5H5h8OPDlTGJJ0CE3HWZL1Ix4N+lv/vz5eNfWte6GG27AD3/4Q2zevBlzYify4447DkceeSQee+wxrFu3DnPnzsWCBQvw6quvjl7Z8DD/JGtaYifqzmZjI+f3piPqDnNjY3qRBvD7/f3Aroh2X7LEZmKLdTvWhU1Uv09WDOm+T9Z71rKCkC3cRKPF8pyPsTsoYlnwisQ6zjv/yd+7FhHNXpF1DnMmJ5gh4M2tnD/rUWezsrIylJSUoLOzE5s3b0ZHRwcWLFiAqqqqUctt3LgRB9m6reXn56OoqAjd3d2osFxMy1UuynD7beZMbmkcRZRyLpibm9lRzxRvGDiNAWDhX1fn/5h0aWwEJk9O//e1LgqievFiCfl0+6Kign+iKvoFIZGNfwb+57zRr10zEs07VUL2Y9VxXncn8PTX+bXfxVI2ro1w1bAsITcdZoDFg8c5zIcccgjeeecdfO9738OPfvQjlJaWos/WIKWtrQ2VlZUoTHCO+/v7UWJvKGGNK5sd5vZ2dl2diE2lojtRy4lgtqczRBEnMVjvRzmGggIW/umYPl0cZiH6WNUv7GL5y+tiE/pELAs+s/BfxwrkmwhYf28448kRRDBrcOihh+Kee+6BUgrHHnssqqurMTw8vE80b9myBdOmjc5Ra2trQ11d3WgRreMwd3XxT9RwcgsdGO3ORo3hYe5EmM0xAM4Ec3Exi9EoxzB1auoyixYimIWo89qvR1e/yC9m8TL58PDGJIxPrlXApbbqSE99ceyEU8ExuS+YPWxecuihh+K3v/0tbrzxxn2vfexjH8OqVasAAAcffDB27dqFBQsW4KWXXgIAPP/88zj99NNHr0jHYQai6QrmgmBuaWHRnCmGyZN5X0VxPwDOBDMQ7TsWDQ2Zc8kBEcxCtLmJgL9/I/77N1uAq/pSLy8IfjNxFgvnCVPir91EwLuPhjemLCV3BbMlRj1sXvKFL3wBIyMjWLRo0b7XvvnNb+L3v/89AKC8vByrV6/G+vXrccwxxwAAHnjgAVxyySWjVzQ4yE5aJjctyhO1ckEwO40hL4+XiWIMfX1AW5szwRzliiVORf/06XxXIFb3XBAiQdOa0c7dpANjIiVDipEgBMU3m4HLbP//Hz1X3GZNcl8w+9y85IgjjsCJJ564r3GJnYGBAZx99tmjJgHG3sjsLgPRzjt1UpkBAMrL+ae52f8x6eJUMAPRdWebmvgxm2NQSs9hHh4Gdu70f1yC4IRbioB7j4z//vUtwNciOllbGN9UTE+e29zXEc54sgxXgpmIPk1EfyKipIVRiej3RPQyES2P/ZzpZntaBCSYAeDiiy/e17jETlFRES666KKxHxgcdFYxor6eH6MqNjNVZrCor49uDIAzsVlfzykcUUM3ho4OnqwZJbq6gD17nDvMgKRlCOGjRlhsjNjOMdcqoHJOaEMSBEdcq4B/eSn++y8mAc9+O7zxZAluHeZWAJcBSKWaZgI4USm1NPbzuMvtOSdAwayN0xJrpaVAZWV0xaYTgQNEWzA7qcwARDsGwJk7a12ARU3464h+EcxCFPhgBTeHsDjjD1K2S8guph89+ju75ueSopEBV4JZKbVCKZWum0MVgN8Q0Uoi+hURlbnYlt4HrHbNURPMSvGYCgudxTRlSvQEDpA7gnnaNM5RzkR9PbeWjpo7q+swA9HbF1bJQRHMQjbw34cBDy6N/35VP3Dov4Q2HEFwxbUKmPvx+O83ETAUsfNcRPA7h3kNgO8ppZaA3ejvJVuIiC4hojVEtKa1tXXM+yUlJWhra9MTzdakuqgJ5tgkRFVQgLa2ttH1mZMRVbHZ1MRi0wlRjaG5OS4iMxFVd3bHjvidiExMic2SjloM1nic7AvrbkDUYhDGBzcRsGt9/PdrFZAfwYZMgqDD+X8DLn4j/vttJcDWZ8IbT0TxtdOfUspeHuJhAL9MsdxdAO4CgMWLF49RxTNmzEBDQwOSiem0tLcD3d2cHxkVBgb2tVguqanBjEy30uvrgXURa205PMwxTJmSeVkg7s729QGZLhCCpKUFmDXL2bJWrM3Nzj8TBDt38ticNEOIqsNsiV8nqTEFBUBNjUz6E4JleBC41SaMj7kBOP6H4Y1HELym7jDuQmnVEH/oVGD2KcBn/x7uuCKEb4KZiEoBXA/gRqXUAIBPAHjNZF2FhYWYO3eu/gcvu4wd3RdeMNmsPzzzDPCJTwArVgCLF2dePorubFsbMDLiTOAAo93Z2bP9G5cuO3c62wdAdMXmzp3O94O1XNRiaGnhnH4nLjkQ3TQlITdpXQ/cfVj893/dBFTNC288guAXRHzXxMpl3vYMP5f8fAA+pGQQ0R+JaKFSqhfALgCriWgFgEUA/sPr7aVl6tR42a2oYDljTt3ZKVO4ikBvr39j0sWKwalQs0rPRUmojYzE3VknRFUwt7Q43w/FxUB1dfRisES/05bBIpiNcVDZ6HwiWk1Ea4notqDHFzleuXW0WL5mWMSykPtcq4AFtgpfMhkQgEeCWSlVb3v+WaXUutjzXyilFiqlTlBKfV4p1e3F9hxTX8+C2cNuf05pbY3PZRqFzu1nINTc2e5uYNOmJG/oiv4QxebAAPDOO6yPR9HRwakluu5sCPtBKY4haad3HdEPhFoeb8uWFF3eW1r0YhDB7IaUlY2IaDaAGwGcCmAxgBlEdF6ww4sQd9QCy6+O/36tAih3WxcIwig++Xvg00/Gf7+JgJHx3TAqt4/+qVOBvXuBnp5AN/vXv3JTtVmzgHvvTXhz504ueVdV5WxlIYnNDRuA/fYD9t8f+Ld/S3jTVPQHHENHB7BoETB/PnDmmQnN4XRFf1ER584GHMPQEI99/nzgiCM4pn0opZeSAYSW4nPddcC8efzz9tsJb+rGMHmy5DAbkqGy0WkAlimldiueYX0ngLODG12EuImA3rb473JLWhiP7PfJ0d0BbykYfVyMM3JbMIcg1Hp7gYsvBg48EPjoR4FLL00ww6xb6E5vP4cQg1LA17/Oj+edB9x0E/Dii7YFdFMy6uo43oCF2g03sDP7la8ATz0F3HWX7U1d0Q+EIjbvuQd48kngq18F3n2Xhec+OjpYUevEMGVK4DGsXg389Kf8XcrP51hG3fQxcZi7u6OVppQb1ACwfzmaAKT8cmWqbpS12G8/1y4QsSyMbyqmA1cPxX+/oxZofy+88YRIbgvmujp+DPCf+e9+x3rkV78C7r6bz+m//rVtAd1b6CGUAvvHP4CVK1lw3nsvUFsL3HKLbYGdO7laQXW1sxUWFvJKAhRqbW0skL/4ReC3v+WLl1tusaVm6Ip+IHCxqRRw883AUUdxLF/5Cn+/9n2dTWIIISXjppvYnL/nHuAHP+Dv174LMBOXPKrl8bKfFowWyPWx15KilLpLKbVYKbW4zvpfm+3YxfKibwFfeTO8sQhCVMjLH33h+NsDgR2rwxtPSIhg9pgHHwQWLACWLGGX+ZRTgPvvtzlqJrefgUCF2oMPcvW3L30JKCvjx7/8xZYO0NLCf1snDT8sAnZnH32Uc36/8Q02ty+7jHNoX3kltoAltnTzfwOM4dVXgfffBy65JB5Dfz+wbFlsAd20EoBj6OkJLE1p9252yL/wBaCiArjoIv5OPfCAbYGBAbOLSEnL8Jq/ADiHiCpiv18M4LEQxxMsdrH8yXuBU34R3lgEIYrYRfMfjgLefzL1sjmICGYPaWoCVq0CPvOZ+Guf+QxPnPvnP2Mv6FQ1ANidDTB3dmQEeOQR4JOfZIEDcAyDg8ATT8QW0hX9AO+LAC9cHn6Yc7AXLuTfzzyT05AfeSS2wM6dLPgnTXK+0oAnmz38MI/53HP598MO44uwfTGYpJUE7M4+8QTr4Qsu4N8nTADOOINjGBmBmUsuzUs8xVbZqAnAjwGsJKJXALQopZZl+HhuYBfLn1sOLPhCaEMRhEhjF83LPgVs+FN4YwkYEcwe8uyz7CSfeWb8tTPOiL+37/azjpsGcBy70nUg947161mbf+pT8deOPJI1yt+t+uUmMdTWBrYf+vq4zPVZZ8VTxSsrgeOP5zLYAOIueX6+8xXX1XETnIByZ599FjjmmPj8UCLeL6tWcYyuxGZA++Lvf+c/21FHxV87/XTe/Pr1MHP6JSXDNWkqG92vlDpCKXWUUuqq8EYYIHaxfNGrwKwTwhuLIGQDdtH8+AXAe4+HN5YAyW3BXFrKllZA4mDlShY3h9nKdk6dyq7g88+Db4P39UXanV2xgh9PsJ0ziPj3FStiqSW6LjkQqOh/9VVOXTgh4bx34onAG2/EhmHqkgOBxNHezg0eTzxx9OtLl3JsL78MjoGIL0acYi0b0L5YsYLTk+xzXK2YnnsO5rnkgKRkCO6xi+UvrgGmOmxkJAjjHbto/vNZwAcrwhtLQOS2YAYCF5vHHz/WtDzxRG42OLzDwE0DWOQEJHBWruRyeHPmjH596VJg+3Zg82aYic3aWlaBQ0OZl3XJypX8eNxxo19futT2vmkMQCD7YuVKvjhJFMzHHceZJMuXgy9camv1XXIgkBi2beOfxAuXWbM4XWZfDIDeMVFSAkycKA6z4I5EsVy/KLyxCEI2YhfNDy4Fmo2aOWcNIpg9YudOLvt1/PFj3zvmGG7YsHFNrG+LiVALSDCvWsWOYCLHHsuPq1f2cW1rk7QSgEWzz7zwAk+8TExPPvJITglfvRr6pcyAQFN8Xn6Zx/qRj4x+vaoKOPTQ2ORFN6I/gBisShjJjomPfhRYswa8H3RdcoDjFsEsmGIXy59fIWJZEEyxi+bfLwK6kjYRzQlEMHvE66/z45FHjn1vUex/8drVsc4ZpukMY9rVeUtzM/8sTnJX8pBDuLPy2hf7+IWICjWlgNdeS74fioo4XWbtWkTeYX79dRbGxcVj31u0iGNQLQa55OXl/IcIKIbiYo4jkUWLgMZGoHlrH09qLSjQW/nkyYFOIhVyiMRqGDOTOASRfexBAAAgAElEQVSCIDjHLpp/MxsY6gtvLD4igtkjrCoYhx8+9r2DD+Z06rXrY+rHJCVjeJhLcPnIunX8aFWWsFNYCHzoQ8Br62Inm4jm/zY38+5OFgMAfPjDwGuvKaieHrP9AAQi+l9/nTv7JWPRIh5C4w7S3w9EgeWTr1vHTn9h4dj3rIuyte9N1I8BYJHdNn47TgmG3GG7k7H4CqmGIQheYRfNt5WGNw4fGT+CWfnbrWndOs7NTNbLIz+fBdza9yv5Bd3bzwGJTUswJxP9AAu1194pgwIi6zCnE/0Ax9DeTtiG2fG/q1OqqzmB2Of90NjIf6ZUgvnDH+bH11qm68cABFKxRCneF6liOOII1u5rGqeaxxBQmpKQI6y4Lt7Wd/JC4OSfhTseQcg1rrHdBbffyckRxodg7uvzvVHDunWpRRrAImdd02Soiol8S1yHgMTmP//Jk/2sMmaJHHEEsHtPIbZijrnoD0gwf+hDyd+3xOY6LNSPIS+PnU2fhZqV3pNKbC5cCBApvN57kJnYDMBh3rGDN5HqmCgvB/bfH3izYwb/TXWprWWH2ecLYSFHaHkdePmn8d+//Hp4YxGEXIUIuKIr/nuOiebxIZgBX4Vaby+wcWN6wXzIIUDPYAkaq5IkdGYioNzZTKLfykV9G4foixxreZ9jyCT6Dz6YHzdgvrlQC+DCBUjt9JeVAXNnDZvtByAQdzaT0w/wMfH23jlmMdTU8IXw3r1G4xPGEcMDwO8+HP/9WrnIEgTfKK4ALra1lL+9PLyxeEzuC+YAGjVs2MDz8ez1lxOZPz+2bEkK2zAdAaRk9PdzlQ9HMeQtYItQh6Ii7h7is9h8883U7jLA1chmTNpjLpgDcGffeQeYOTPeaTEZ82f34h0cHFnR/9Zb/LhgQeplDpmv8N7wXAxWGaZkAJKWIWTmVtvMWRHLguA/dQuAE2/j54N7gLW/Cnc8HpH7gjkAh/ndd/nRci+TsU9s5qdREKkIICVj82YW/QcdlHqZSZOAySVd2FB8+OhOFE7xWWwODwPvv59+PwDA/MltkXaYN25Mvx8AYP60TmzEQRiuMhT9nZ3c79wnNm4E6uv5GikVh8ztxRAK8b7aT38D1jEhE/+EdNhvCV8zHN44BGG88ZErgbxY9aNnLge6d4Q7Hg8QwewBGzeyftwvzXl/yhSgKm83NgwdoL+BsjJu1uCj2LRE/4EHpl9u/oQPsAGHmG3EZ7H5wQfAwICDGCqb8A4OhqqelH7BZPgs+pVyJpgPrt6JfpRga/9U/Y1YYtPHmtjvvpt5PxxSz9t/u3eu/gYCSvERsphfz4w/v/gNgHL/dCcIkeJqmynz6+nhjcMjcv8/SEAO86xZXDouFUTAfHoHG3pn62/AKgXms+gHHIjNwvfxzuA8s7lWPotNx6K/dAt6UIGGZs3av0B8splPNbGbm4HubgcO88QGAMCGNsNJf4Dv36dM++GgKm488laHC9EvDrOQjO0rgW4+RnDgOUBdmlwzQRD8w54GleWTAHNfME+YwN0TfDyxOnHTMDSE+cPrsaHTQBwAvk/UevdddsHT3UIHgPnqbXQMTcTOnQYb8dlhdiyY83nBDRsMNmLVxO7sNPhwZqwYMgrm4s0AgA07UsxuTIfP+b8dHbybM+2HCXtbMQvb8F6bgdMvDrOQCqWAB2z92M/5c3hjEQQB+JZNf9370fDG4ZLcF8xEnHzrk2BWyqFgbm/HQdiInXvK0dWVYdlkBCCYM8YA4KD+NwDEHWktfK6J/e67PKkvU4noA4dYKb//vsFGfJ6Aaf1dMwnm6r07UIedeG9rkq4gmfBZML/3Hj9migFtbdgPm7CpJc3sxlRUV/OxLYJZSORm22lNJvkJQviUTgKO/i4/b3oFaH0r3PEYkvuCGWA3yqd8zZ07ga4uB2KzrQ3zwK7gli0GGwogJSNjDEphXjfXPDOKobaWk4x9qoltif5M8xHru99DSV4/Nm822IjPEzA3buTUnpkzMyzY1oZ5hQ3YvMVw8iXgawyAs2NiP2zCpsYk/b8zUVDAollSMgQ7v7RdLV/hb2dUQRA0WHJj/PndBsUPIsD4EMw+OsxOb6HbBbOxUPPJTevsZOGfUeB0d2P28CYQKXPRD/gm1Jy65NTehnkVre4Es0/74t13uaFHXqYjs60N8yY0m8XgczrDu+/y+OfNy7Dgrl2Yhy3Y2ZqH7m6DDQXQREbIInZvA/bG/rccfglQPDHc8QiCMJosz2ceP4LZJ4fZuv18QKbiF24Fc10dW9kDAwYfTs+mTfzoJIYiDGLmpD1mMUyK5ap2dBh8OD39/cC2bQ5iAHhfTOo03w+Ab6J/69b01Vb20daGeZXt+OADYGhIcyOFhb7WxH7/fWD2bAcNLdvasN+EZgDRu4gUspD/Nyf+/LQ7QxuGIAhpuKwh/vzVn4c3DgNcCWYi+jQR/YmIPkjx/vlEtJqI1hLRbW625QofUzK2bmU3LeMt9F27UIXdqK4cjpzY3LqVH+fMybBgzKWfN7XPXQw+7Ivt2zk1OqOrOTAAdHdj3pQ92LTJIJ3ax/2gFO+LjPsBYMFc24XhYY5dm9pa346JbduAuU4qxbW1Yb9J/He0Ltq0sCqWCILdrZK8ZUGILhXTgcmxNrbPfdu3OU1+4NZhbgVwGYAxXhIRzQZwI4BTASwGMIOIznO5PTOslAwfdszWrcD06WzapcUSm/MM3TQfxaa2YJ7tUvT7GMPsTFX7rBhmDKKnx8CgnDCBd7YPMbS3c3q3Y8E8rQ+A4feputrXi8iM+wFgwTyF89mNU0t8cph9qhoo+EHTq/Hn5z4W3jgEQXDGl9fFn9+cPYkOrkaqlFqhlEp1xjoNwDKl1G6llAJwJ4Cz3WzPmJoavmff2+v5qrdtcy5wUFSEefvnRU5sbtvGbZirMlUos8Tm/nloagL27tXckBWDD67gtm386Fj0z+OLJ+19YVVdCfPCRSmgvR3zZnEuhvH3yYcY+vqApibnx0TVlGJMmhQ9h/mgg4DLL/dl1YLX3PuR+PMDzgxvHIIgOOcKW7mwl/5veOPQwE9pXwOg2fZ7E4CkBb+I6BIiWkNEa1r9yKv0UajpuGmoqcG8eYStW7mUrxY+u7Nz5jjodm2JzfnF+z6nhc8x5Oez258WK4YD+ZZAlMSmY8G8ezcwPIzpcwpRWBitGKz0EMcXkTU12G8/Q8FcU8MXwdpXbukZHuZ9UWFQ7U4IGEnFEITspLgCmHUiP3/hu+GOxSF+CuYWjBbI9bHXxqCUuksptVgptbiuzqBzWSasqgAeC4ShIaCxUUMc1NZi3jxOo92h21bdZ4fZcQwA5i0oA2Ag1IqKgPJy32KYMYOrjaUlFsPcQ7gto5FQ81kwO00rya+bhDlzXAhmH/PhHV1E7toF1NZi9mxua66NTxVLmpr42HYUgxAevTYD5OMyyU8Qso7PPRd/ngVVM/wUzH8BcA4RWT7NxQDCSTDzyWFuaGA3SsdhtoSpdlk2nwSzNdHMcQxVVZh7AKtSo9JyPopNxzEAKJsxCZMnx1M5tPAxhqoq56kxqKnB3Lku94PHybqOXfK+PnaGa2owaxYLZu0pBtaFsMfHtSXeZ83ydLWC19xRG3++8JLwxiEIgjmX2k7CEW9o4rlgJqI/EtFCpVQTgB8DWElErwBoUUot83p7jvDJYXYsDoB9gtmqpqFd2WDiRC7H4XEMnZ1crU4nhro67jZuVJ3BJ7Gp65JbQi1KMehUyACw7/tkHMPICMwKIKdGNzXGiqG31+BP6tNFpHURJQ5zhFlxffz5NTJDUxCylok2ZyLiDU08EcxKqXrb888qpdbFnt+vlDpCKXWUUuoqL7ZlRBROrLt2uRPMeXm+VDZwPFkO2CeYiTj9ISpic3CQ3X7HDnNJCVBW5k5sRkgwt7QYlOf28ZjQSY2xLlwAg7QMn0r8iWDOAl7+CT+WT3Uw+UIQhEhjn3/waDjF1JyQPfU83OBTSoblMGe8dRuraoCaGpSXs+6NilDTyjmNCWYAkRKbjY1sljoSm7G8WcBlDD09njaR0a3BDGCfYFaK/wZa+CSYTWIwFszV1fzog+ivqeEKgkIEsec6fkN3MoggCJHk2O/z47t/DnccaRgfgrm0lH98OLFOncrpCWnp6uJZRBEUm1ppJV6JzQiJ/u5uLjqhhQ/Opm4NZhABVVXmdyyiIphrayPnMH/wgeQvRxZlS7/41P3hjUMQBG857gfx5xGdADg+BDMQb17iISZuGhAtsbltG1BWFk/zTkuC2GxsNCyP197uaRMZk7QSAJESm5ZYzNgxEuAYqquB/Px9yxuLTQ9jsKq/OE5RAtzlxJeWcuUVH44JSceIKDfnx58f8vnwxiEIgvd8cU38+chQeONIwfgRzD60x3bsREVYMG/fzjFkTAMcGGAL1BbD8DDQ3Jzhc4lMmsRJx3v2GI03GZZYnDHDwcJJBHMUxKaVUmEaQxRE/44dfB3kSPRb2500CUT8Ge39YDWR8dhh3r7dYQxCsPR1xp9/M2mFUkEQspn6RfHnt2Rqnxw840cwe+wwK8UCIWM1AGCUOAD4ZNzWZtgpz4f8X9MYgGgItYYG7HMpM9LeHtkYAIf7wiaYJ0wwzIn3If/XEv2OYujoYIe4pAQA9pWW08bjibA9PZxB5ejCRQiWX1THn09I2gNLEIRsx94BsNf7yfVuGD+C2WOHubOTS2E5FgfAPpHiSqh1dhrkQaTGsWC2YkgQm1FwZx1fuCjFccT2w9SpXAItCoK5sZELoUyZ4mDhjo74GGB4x8KHJjLagrk6LoCMBbPHDrMVw7Rpnq1S8IIu2xf8O33hjUMQBH8ptrVYvcNJrmhwjB/B7LE7qy0OAG8EM8Ci2QNGRrirmVYMsa4aUXJnHYv+PXt48mVsPxQUsDCKSgxTpzooxwbwvrB1N4lKio/2MZEQw44dnK2jhccOs1YMQnD8xpb7VuDkVpIgCFnLVbYKVH3e6B0vGF+Cua3Ns8lmoQpmjwTCzp2sH01iqKridICwYwAMXHKbs2kkNn1oIuM4BmCMOxslwVxcPMr8Tk0Sh9lKc9LCJ4dZBHOE6GmKP786ehOBBEHwmHxb/rI9FStkxo9grqnxdLKZ1om1s5NzNWP5mlZ+ZNhi043otyZqacfgcTvjgQEW/o73A+BebPrQRKahwWEMIyMcR4LYbG83yIn3wZ2dPt1hH4kEwWzFri2YxWHOff7Tlh+Tl596OUEQcgd76tWg7snNH8aPYPa4eYlWrmOCOCgu5lzVrBLMXolNjyebNcXMJ7cOs/aNBx/cWUcxdHfzYBNiAAy/TxFxya3jyMhh7u7mWyUe0NgIVFZK05LIYC8t9Z3e8MYhCEKw2FOvbo/GP+TxI5g9djYbG7mHh6PKDAniAGBhYSQOgHAdZlve6YwZBh3mPG4i4zaG6dOB/n6Du/oeis09e7h5iqPKDElEvxW7Ube/sARzgktuLJitdXiU168VQ5ZCROcT0WoiWktEtyV5f3nCz0fCGCeA0aWlCkpCG4YgCCHwf6RKRjiEeWJNmOAE8ASvKAjm/HyNygwTJgCF8RPYtGlAS4uL5iUeoO30A945mxER/VYMTU1Jlk+Hh01krPbcjmIYHuYrBNt+qKnhr1YUjolcFsxENBvAjQBOBbAYwAwiOi9hsWKl1FLbz+rAB5rIJe+HPQJBEIKmxGY03hS+XA1/BEFhnZw9miDk5vYzwCJHW+BYIslDcVBfz6I5I0limDqVtU9rq+aGwxabtjimTuXHMAWzVg1mr2MYGDBIfh5Lezs79Y5isHqR22LIyzO8iAzzuM5OTgOwTCm1WymlANwJ4GzrTSIqAFBJRH8iopVEdCMRhZM4bG+PW71fKEMQBCFkPvPX2BPvugObMn4EsyU2PTyxOq7VmkIw79ypWUaroIATLMNw01LEALhwNj1AqzJDZyfPSKus3PdSVGIAzHPJKyrY/A/TnXXrkgO8L8KMwepcmeOCuQaAvT9nEwB7F5ByACsAXAJgKYCpAL6abEVEdAkRrSGiNa3aV80anPBT/9YtCEK0mXda/PnL4f4vGD+C2cOUDK3KDNY2k7izSnFKgxYeCzW3MQDhpzNoVWaorGQ7M4arGDxqIuPWJSfiOIxEPxCeYE5yARamw2ylF+W4YG7BaIFcH3sNAKCU6lRKXRp7HAHwZwBJc5iVUncppRYrpRbX1dV5O8qtz8aff/Rab9ctCEJ2Medj/LjiulCHMX4Ec3k55x54cGJtjvkzjsuAJeRrAtFxNnPBYXYTQ1kZa2hjZ9ODC7DGxnhd64xE1J0NTTCHFUP28hcA5xCR1U7rYgCPWW8SUT0RXU+07xL0NACvBTxG4KFTAt+kIAgR5YKn48+H+kMbxvgRzEQsMjwQzFon1t272UpOMukPCM+dtSozuJm4WF/Pj0auYFi55AkxAIb55B6WKXRcgxngGPLzOQ/DhqsYPBSbppMvrc92dmqmVHuYajUeBLNSqgnAjwGsJKJXALQopZbFqmFYbnM5gNeI6AUABOCu0AZ8jfs7OIIg5BC3hVctZ/wIZsAzoeaVmwaE585qi4Mk7mxREZfWM5q82NvLs8RcoFWZAUgaA+AyFcAjh1lb9CfkoFgT5rQKXngsmCdP5u9ERpLkYQOGx0RhIV88iMPsGKXU/UqpI5RSRymlroq9tlQp1ayY62PvH6+Uulwppduw3B32yX40vk5RgiCk4OL1YY9gHApmjwQO4E4wT57MqbTaQi0Ml3xoCOjpiZzY7OgA+vrcC2aj/F/L2QxaMCfJJQd4P+zdC3R1aWzYw/xfbdFv334MV7WYPYqhoICPTSECHHND2CMQBCEq1B0af77pL6EMYfwJZo9OrMXF8V4oaUkhDqwTs7ZQs0S/y9q5WrfQUziCQLhiU9sRTCM2td1Zj8TmyAhPNrNSdDKSRvQDmvuirIy/iB6Jfq2qMUVF3MDGRtg1sRsb+e+YN77+K0aLIVs73ON/GN44BEGILo98MpTNjq9Tg0fubFMT5+86qsyQRmwaubNVVVyLrtddm1hr4qKbnFPr82FVNrDEoVuxOW0aVz7R0lweif62Nq7MYOWDZyRNHjaguS+IPLuIbG7W3A9J0kqsC5+wHObmZg3RL/jDbaWZlxEEYXxy9VComx9fgtmjlAxtcWBtO4EwGzU0NwMlJWPmjiUnRWUGgGNobtasruaR2LRK8jnaF319/OOVO+vRfrBicNRt0dpeCtEPGLr9LveD1bxGS/QniaGykk3nsBzm5maN/SD4y2f+FvYIBEGIGnm2HkpvPxj85gPfYphYTpTLdIaWFk2BA3hXncEjsdncrOGSZ3CYh4eBXbs0Nu6h6Ac0WnsD3rmzJSWcVuDBfgDci03jqiseuLO7dnFqidsYiHhfWKk2jvHQYXYcg+A9A3viz+d9PLxxCIIQfZ74fOCbdC2Yieh8IlpNRGuJ6LYk7y9P+ElaBD8QrHQGl62AtU6sHR2cJ5qkyK7V7W9I5y6Dh86m4xgy5DADmkLNo1Jgzc2chlte7mDhDKIfCCedQUswK5UyD9u4258HDrPWhQuQUjADLmoxu3SYrYs+Ecwh8jMnB7IgCOOaENMyXAlmIpoN4EYApwJYDGAGEZ2XsFhxrGSR9bPazTZd4UF1hqEhzROrJQ6SWLlG3f48dJi1XXKvUgEi5pIbpWQAnohNrZSMvXv5gi+FO2s0ATNo0Q+kFP2AizSl/n5Xef2treySS0pGBPh4eGWfBUGIOPa0jIYXg920y8+fBmCZUmq3UkoBuBPA2dabRFQAoJKI/kREK4noRiLKT7Uy3/HAnW1tZZHr9vYzYOhsepjOoBWDfds2jNMZSko8cckdC5w0LnlpKWvfMNIZrFzyiRMdLJwmrQRwMYnUI9HvxTFRX2/YLh5w5TJri37BPxZ+LewRCIKQDdx/XKCbcyuYawA0235vAmCvYloOYAWASwAsBTAVwFcTV0JElxDRGiJa09ra6nJIafAgFUD79nMGNw0wTGdwIXIGB7k6g5bAKS5mZZeAtQ7j8ngu8Er0A+GJTa9ccsBFiT+Xef1aYnNkJO0xUV/PtaS1zGIPLiJFMIfMI58KewSCIGQLl24LZbNuBXMLRgtkq7UqAEAp1amUujT2OALgzwDG5DArpe5SSi1WSi2uq6tzOaQ0hHFideAwG6UzRMQlt7r9hdGAxUvBHFY6g1cuOeCinrTLMoVaueTd3SyaU7jk1t9Cy2X24LjWdskFb9n0JD/mFYY7DkEQos/EWfHnLos46OBWMP8FwDlEZBUnuxjAY9abRFRPRNcT7fPPTgPwmsttmuNBDrORYE4hDqxrAy1xUFDAysSDGLxwyQH+WzQ3p3w7OS4dZssl187DrqxM+vaUKQapAB46zI7IIPrr6znNuadHYwAe3LHQmkDqIAZA8/vk4YWw5DCHzHfc1ZcXBGGc8afTAtuUK8GslGoC8GMAK4noFQAtSqllsWoYlttcDuA1InoBAAEIb0aHh06UFxUBCgvZnTUSm0G6aWliAAzFpssYdu7kR60Yysv5j54EY9HvMp3BqERhin0Rljvrtei31ukYj2IoL09azEbwmxHbrPe88Ka4CIKQRcw5lR+3/m9gm3RdVk4pdb9S6gil1FFKqatiry1VSjUr5vrY+8crpS5XSg26H7Yhlrvo8sRaUcG3oDOSpgyYRRjOppcuOZAlMTjYD0bu7PAwsGdP5mWTMDRk0PDD2m4SrPUEXXXFq4orQLgpGZKOERK/mBT2CARByDbOD7650fhqXJKfz+UIXIoDxyfW7m4WVH6kMwR5+zmDwxxGDF46/UA4zqZRLjmQNq0ECMed9aKmNwBMnhxfp2MqK3nWpMsYJB0jJAa6+XHSweGOQxCE7IGCl6/jSzADnohNryZpAeG5s45dcsBRSoaRO7t7N08AM8DLyZeAobPp0p3VFv2dnSwO85Pftg4jhoEBrubmVUqGUZpSXh7/XYIS/YI/fPWtsEcgCEI2svzfAtnM+BPMLqszeDnBCXAhmIOKYWSEha3XYrO6mtfd3a3xoThGLnmGtBIg2FQAr0V/XR0brUHGYJRLbt9uEsLIiZeUjAgQgmMkCEIO8MpNgWxm/P2HclmdwWiCUxqhVl/PKbBa7myQMXR1cd6A1+kMLp3N5mbOriktdfgBP1IyPIjBvu2MZBD9BQUG7qyV3uEyBq0Ll/z8tDXojFN8DBuX9PfzRyUlIwTefjDsEQiCkK1c1hjo5sanYDZ0ovr6WFd47aYBBrfRu7o4P9oAo0laEXNntR3BDIK5tjZ4d9brPGxrXVoxFBayeHUZg7boT9OpZcqUYHPitV1ywTue+HzYIxAEIVupmBbo5safYHaRzmCdWL2qCGBfl9FErd27NT4Ux4+0EsDQnXWRzuA4hsFBtvHTxFBQwCkNQeb/apcycyCYjVpLu8iJ9zqtxFpXS4tBA5agUmME71ny47BHIAhCNhNAA5PxJ5iDPLE6mPQXdCkwbZfcQQyucmddCDUvJ18CBs6myzKF2pUZMpTGA4J3Z72uuAIYNmBxEYN0+YsAR18X9ggEQchmVl7v+ybGp2Deu5en92ti5Kbl5XFJihQEXQrMKA3Avs0kWLmzRqI/iJQMBzEABukMLssUep1WAhi6sy4c5pYWvm4oKXH4AYei31q3Y1w0kZEuf4IgCFnOyz/1fRPjUzADRgLBuDJDXuo/s5E768JhNso5BRwJNSPRbxBDby9no3g5+RIIvp60VlpJfz8HniGGKVN4Ma3iIy7SlLTLsTkU/da6HVNdzRfBvfqtlUUwh8RQf9gjEAQh2znr4cA2Nf4Eswtn0xKbVnOFjGSoagAYurMuHGYjlxxwJNS0Yqio4AsJF/vBL4c5SHfWS6cfcOHOukiN8Vowh3HXpboaKC7W/qjghic+F/YIBEHIdg7+dGCbGn+C2aXDPGmSxonVgTgADPJOXTjMRoI5QxkwwCAGq9lEUE4/4MjZ7O0NJnfWKmXmZS454CInPgjRr5Sji0ijGFxeRIq7HALvPhr2CARBEBwzfgVzECdWh4JZu7KBBznMjl1yK+c0TRkwINjKBtoOs8akP8Dg4sVAbPpRccW+Pm13dvduozKFWg7znj3A0FDGGGpr+XoqKIdZuvyFzEGfCXsEgiAIGRl/gtllSobWidXBBCfAwJ2dMIFdXxcueVGRww9ouOTa7qyh2DROK/FzspkmfuaS29fvCOuY6OrS+BDv764u72PIz+fc/iBTMkQwh8gn/jvsEQiCkAt07/B19eNPMLtMyfA6XxMwcGeJjIWaXzEYO5su8rC1cslLSzPm0hh3+wtS9GdIZ7Dc2SDuWPgl+q11BpmSIYI5RIpTVxESBEFwzHNX+rr68SuY/T6xWvmaEXNntXJOAUc5p0CwubMtLUBNDTepc4TDGIwd5p4ebo6igV952Pn5Bu2xDXPitWNwmBoDuKi6onlc79nDFUUkh1kQBCHLeechX1c//gRzcTG7jZon1p4ePrk6PrH29nKZKw2hFpQ766fDHEQ6g18xGLmz1v7V7LqoXQ9bU2wG4c76lRoDBNdERpqWCIIgZDkTgvkHPv4EM2BUd9bv28/2bTjCRSqAX3nY1vod4yIGrzvkAcHmzjY3c/iOG350dHDuugNbXbvEn0uH2c+UDMdpSvn5LJpFMAuCIIwvFl0eyGbGp2A2qDvrt5tm34YjDES/5ZL7kVZSV2eYO9vbyzXWNPCjQ55FkGLTj4orQHDpDNbfqa7O4Qc0j4mBAc0/q8EdC2laEhId74c9AkEQcoXDvxbIZsavYPb7xKpxCz2oZhPaaQAOy4ABLnNnNfaFUv6lZADBpTMYiX4H6T2AQQMWF6K/tlYzl5yI24lnwLjbn99pJYI3vPm7sEcgCEKuUObUtXHH+BTMBu6sX1UNAEN31iCdwc8YAAN31qBiSU8PsHevPxMXgeCayPjpME+ZAiDdHT0AACAASURBVPT1abTHLi/nKx6DY0Jb9FdWpm0VbxGUYG5pYQ3v2CUPGCKaQET5YY/DczY8GPYIBEEQtBifgtnQnc3L0zixajjMRu5sdTWnMvT2Ov6In3nY1nqN0hk0RI626B8Z4WLBmikZjt3ZoBxmh3nYgIHYJDK6APMzhqAmkVoueUGB1sd8g4jyiOjzRPQUEe0E8A6AJiJ6i4huIaIDwh6jJ3RuDnsEgiAIWoxfwWxwYq2rY3HriKDEpobI8TOtxFqvUe6sRgzaon/3bla/Gvuhr0+jh4fBfti7V7PhB6DtMAPBiE3tyZcOnX7j9th+u+T+8zyA/QBcB6BeKTVTKTUZwPEAXgbwUyL6lzAHKAiCMB6JiK8SMFVVLKRGRhzdHgYMxQEQL3eVAWOx2dEBTJ3q6CPNzZouuWZKhr2yQYZO2oyBO2ss+jVSMgCOw9GuKy3ltokaMWjnkgNaaSVBNGDxO5e8uppzo4NIyYiYYD5FKTVIRLOVUiPWi0qpdgDLACwjIqdZ44IgCIJHuHaYieh8IlpNRGuJ6LYk73+LiF4lonVEdJXb7XlCdTWf8TVq5xpN0qqocHyvN4jqDC0tmi65gcPstzvrZ7US+3od7wuDdAZtl3xoiBOS/XSYNWPo6eFsIO2UDIeiPy+POzn6naYUNYdZKWV1wHk08T0i+mjCMkZk5f9sQRCEkHElmIloNoAbAZwKYDGAGUR0nu39YwF8DsCxAD4C4GwiWuxmm55gkArg5+1nwKDurKE7q+1q2reVAW2hZpDDbOWS19Y6/IChw+yns6kt+q0LO4f7oabGsMSfn04/oOUwA/5XLLFc8iiVlIuJ2Z8CqCCi+QkT/u7yYP3Z+T9bEAQhZNw6zKcBWKaU2q2UUgDuBHC27f0zANyjlBpQSg0AuBvAWS63OYbvfx845hiNDxieWP26/QwE584apZU4KAMGGLizVtdFzRj8zCUPwp31O60kP9/AnfU7BkD7ItJVmpIDurv5mIuSwwzgRQBvA6gGcDuA94joNSJ6EoBz6zw1kfifLQiCkG24Fcw1AOyntCYAkzXeBwAQ0SVEtIaI1rS2tmoPorcXeP11g7qzDk+su3dzEwW/HWZAQyAYOMwtLY7TnePrrqx0rE6Dcme10wAAx/uitpbD9TMGS4xPHnMkpEBT9AOGJf4MYnC8LwYGeLZjhBzmKDYtUUo1KqXuBXCWUuoTSql5AE4B8H0AJ3mwCU/+ZwPu/2/zSnKvYp4gCLmJW8HcgtH/TOtjrzl9HwCglLpLKbVYKbW4zqAgqrY7q5mSYdTcwMBhBgzSGRzGYHT72VD0a7uzmkLNyCXXzJ3122GuqdFo+KEZA2BYdaW/nw8kB2gfEy5iGBnJvCwAbcFsNPnSZ4h4uqxS6kXrNaVUu1JqrVJqj30ZQzz5nx0bl6v/27ySYbPPCYIgBIxbwfwXAOcQUUXs94sBPGZ7/zEAFxFRYSwX74sAHne5zTH47c4anVj9dpgLC4EJExzH0NXFesjPnFMrd1bbndWcMKcdQ14eT8B0iFEqgJ8uuYHD7Hd7bCuXvKbG4foNXfLhYaCtzeEHDB3miKVkPE9ElxPRLPuLRFRERCcR0e/B/0dNicT/bEEQhGzDlWBWSjUB+DGAlUT0CoAWpdQyIlpORPVKqTXgf7avgGuIPhF7zVO0nU3NlAzt28/WujUFjn1bjtBwNo1dcg3Rb5Q7qyE2jXLJrQsXDVNOW2xaLrnDnCCjhh/WdhxiiX6/2mO3tPC+1q644ucdixxwmME5xsMAHiCiHUT0NhFtAfAeeDLez5RSvzNdeVT+ZwuCIGQbruswK6XuB3B/wmtLbc9vBXCr2+2kQzt3VrMVsHauo1UGTEMc1NT4mztr7JIfoNdYzCgVYP16R4sa5ZJrXrgAHMNbb2l8oLqardA9e/i7lYHmZuDoozXWb+gwDwzw38zR19DAnfWz4gow+rhesMDBBwwuhLVc8gBQSvUB+HWsOclFAN4C0KuU0mvDmH4bof/PFgRByDZyotOfUStgjVSAlhYWs45PrFYZMA3BbFR31sBh9qtZhoVRKoCfTr9magxg4M5qiE2lDB3mggKgrMzxR7SPCQOH2c9ccsAghvx8ruiiIfq1XPJg+RqASwHcB+DgkMciCIIw7skJwTxpEusJv6oCWLefHTYF1G74YWHkzvotNjVjMMr/7epyNLMriNq/AP+NBgc10pI1BHNPDxeLMIpBI61E+66LgcMcRB424O9xHbF0jH0opd5SSp0H4GoA3yWiJ4loYdjj8ozKuWGPQBAEQYucEMzG7qxft58N3DTAf3dWyyUfHOQUA4MYtBuwOOy6GMTkS8CFO+tgXxjlkkcsBssl9/uYmDiRS3X7dUxErWlJCt4HNxppAJA7ucSHfy3sEQiCIGiRE4IZMBSbft1+NnDTAH+rM1i3n4NwybXcWb/FpoHDrF3iT8OdNZ5AaiiY/YjBuOJKcTFQUuL4I0SGtZg1LiIjViFjH0T0HBFtB7AWwPUAOgB8KdRBeckRl4Y9AkEQcoXd2wLZjOtJf1HB6MS6daujRVtagEMP1Vi3C4fZqjvrSNha6QzDwxkTMY1Fv0H+L8DidtIkBx/QFJtaLjkQjDurUdfb2GHWFP3V1Vx5ULtMYYRisLahfRH5zjsZFzNyyYPlKgAblFJedPeLHiV6x6QgCEJKXv5JIJvJGYdZ2511mJJhdGI1dJjr67nAhnburIN0BuO0EoMYrO05QkNstrRwW2zHLnlfH/8EFYOGS+735Esi/+5YGKXGGMRgbcOPGHbvNnDJA0Qp9VrOimVBEAQvWXdnIJvJGcFs1BXMQe3czk4uz+V33VzAX6GmffvZ0GH2MxXA77bYFlVVQFGRRgwTJ7JCdbgf8vK4BbdjXLizfqQzBO0w+xGDUWqMIAiCMG7JKcGs7c4ODXHJgjQYu2kFBXyLWwPtygYO839dTdKKkDsblNOv7c7m5QGVlY7FZl2dRikzpYJzZx3edQlq8qW1jdZWPlQdUV0dv7OQBiOnXxAEQYguH/6Gr6vPGcHsVxktoxOrQXc5wD931sglN3SYLXfWj+oMQXTIs/CrYol2DL29PIsyqPxfv3LJDSZfAhyDUsCuXQ4/4PCYEIc5QrRlzjkXBEHIyJIf+7r6nBHMfpXRCqIttoVf7qyxI2jfhkMsd9ax6J8wgd34DDnMrnLJgxLMDifMBXHhAvB2du7UTFNyGINWxRXA2GGO1DEh+MMfTwl7BIIg5ALFE31dfc4JZm13NoNAcOUwa1JZqVl31s8YOjrYKtYoA2ahJTatrosOXfIgRD+gKfqtbThMyQgqhvp6LqDS1ubwAxoOs1YMShnnMPt550jbJRf8oacx7BEIgiBkJGcEs18n1pYWNkAdlUizMHSYtd1ZP28/WwJHM63E2o7XqQDGE80AV+7s8LDDDziIwagttguH2eiY6O7OmDCsHUNPD/8hXTjMjo8J60B1cExou+SCtyy+IuwRCIKQ7QwPBrapnDldaLuzGikZQd1+BjTFZmkpu8B+5GEbTjSztuN1i2/jyZfW+jWpr+dUBse5sw5icFVxJcgUHwd3LIKYfAn46zBLOkbInHRb2CMQBCHbeeqLgW0qZwSz1RUsEidWF2JTO53BodjUdskNb6EDhu5sBpFmnIddWspXUpoYdfvz68IFCMaddXARGVRbbIvyck5z9+OuiwjmkKGcOf0IghAWGx4MbFM59R9Lq2ZrZSU/OhBqWo6gi3xNwJ/cWSOX3DCtBDBwZ/1KyXAZg327Gamu5k4YacqZGU8gtdaviR/urKuKKy72hR93jqRCRoQYcVo3UBAEIQnH/sD3TeSUYNaqO5uf76h2rrYT1dfHisKFw9za6m3urJFL7iKtxEioOdgP+fkGLrmL/QB4KzZd5WFbF3gaVFSwwe5lSoariisuvk9ax/XEid675IK/LDsz7BEIgpDNHHuD75vIKcGsPdksQzqDq0laLt3Z1laHH3CYzqDtpnngzmqlAmToumgJnKBccj/cWeM87PJyoLBQ40OMlabkZTqDq1xyF98nL++6GFVcEfxl81/DHoEgCNmMQYECXXJOMO/a5V3ubEcH94wI0k0zcja9dpittJIgYxge5moKKQjaJS8vB8rKvM3/bW5m3aulG13EAGi6s3675EHk9QMZjwlpWhIhLlwV9ggEQchWNj0V6OZySjBPmWLgzkbMTfN6stnICE/A04rBKgMWZP4vkDEVwGjypWEMfkwitUR/UC454H3+r6tjYqJZUfkpU4D2dnaFHZHhmJC22BFixrFhj0AQhGzlkTMC3VxOCWajbn8RdNPs285IVRVvM0U7N8slDzIGbXfWodjUdgTDcGe9Fv0uY9AuU1hcnHE/GFVcqazk/GIDrP2+c6fDD/hxISz4z16nTocgCIKNpbcEspmcFMxeubNhOsxaQm1khBtOJCGMGABvnU2lDFzykRFX1UoA7/N/jUS/Bw5zWxtfNDnCwTFhVHHFpegHvEtTMroQFvznl5PDHoEgCNnIUVcFspmcEsxGYjONIxiGw+x13VnjLn9AcM5mhhiMcsm7u1lpBxWDwxzmMFxypbybRGrskrsQ/V6nKRlVXBH844Czwx6BIAjZxh6ntxy9QwTz3r0pkyNbWgwmabloNGFhJDZTiBxXzTKCcpgdxhBktRKA/2ZtbQ5zZwsK+GonhVAzyiUHPHGYAW/d2aBFv1EMvb0pa2JLW+yIcc6fwx6BIAjZxq+Cz6kzPmUQ8xMieoWI1hHRhUmWKSCiXUS03PZT5G7IqSkv5x+vKhtYJ1ataiWdnWwRG5QBs/DSnQ2jbq61Pa9d8qBj8DJ3tq2N51Fqic2hIXbKPYjBS3c2aNFv5DBb202CkegX/MP+D3aPTv1AQRDGPR+9LrBNufFYPg/gAAAfBbAEwL8T0dSEZWYC+F+l1FLbj9O57kZ4OVErjJxTwNvcWaNSZh45zI7d2YkT+aSZJgZrnY7xUDBr7YsU3yWj1Jjdu+PrNUT7rkuaibAjI+FMXCwp4TmDXl1EimCOML+SHSMIggYn/DiwTbkRzGcAuEsxXQAeAXB6wjJzAEwmor8S0QtE9FkX23OEl+7sjh3AtGmaA3ApDgBN0Z/BJW9q4r+J1u1nS/QZlgEDNN3ZvLy0XRd37OBHrX3hUUoG4E06g1FqjEdOv337Gcngkg8OGhwTHl1EhnpcC/5y+j1hj0AQhGwh4PrLFhllFBGdlJBSsZyIlgOoAWA/hTUBSJzmvBfAcrC4PgPA1UR0SJJtXEJEa4hoTavj2UnJ0XJnM4jNHTuAqYmeeSZcVgQAOIb2dqC/38HCfoiDjg5XZcAAb93Zpqa4y+gYDx1mL9zZsPKwy8r4ukdrP+zenbRMYVMTP2p9nwYHgT17PLmI9OKuy9AQX8RpH9eCvxz2pbBHIAhCthBw/WWLjIJZKfVcQkrFUqXUUgAtGC2Q62Ov2T/7ilLqR0qpYaXUbgDPAliUZBt3KaUWK6UW19XVuQrIq85mg4NcWcDIYfbATQMcurMVFSxsI+iSA944m1YMWrnkHjrMXuT/huUwW9vU2g9KAV1dY94ycvqtGCLiMO/cydcC4jBHmKe+FPYIBEHIBi4PtlKGm5SMxwB8BQCIqAzAuQD+al+AiI610jCIqBjAUgCvu9hmRozc2STOpnVyDlNsOhJqRPHmJUloajJ0yT0S/V64s01NhvuBiC8oDCktNcidTRPDhAmaWS4eiH7AO7FpCWat75NHot+rvH7LJReHOYIUlvHj+t+HOw5BEKKLvcFRmTuDVRc3gnkZgB1EtAbACgA/VUo1EdFCIvpjbJkNAM4lolfBqRl3KaXWuxpxBrTc2TQpGcYn1jDEZgqh1tvLL+eCw2ycGuOydpi2O7tnT9IuIY2NBi65h2LTC8FsdEx4JPqnTOFMkd5eBwunOa6NXHIhGL7dE/YIBEGIOiE2ODJWE7HJft+JpVIcqZS6P/b6OqXUZ2PP25VS58feP1op9V9eDTwVWu5scTHbiF6dWEdG+Fa2BwIHcC82jXJOAU9Ev5Vz7EUOc1hpJYB39aSNc8nt6zVEK/83g9icNIn3rWM8FP2AwzgKCvjOggjm7MJ+Nfncd8IbhyAI0efzKwLfZM6V7rdOrJZYzEgKoWbkpu3ezfmfHggcQFPkeOmSeyg2tfZDkhi6u4GennCcfsC7SaTGoj8/n3M5XFBfz6tK0cdjNBkcZqP9YF+vIV7lkzc1sS7TLo0nBMurt4c9AkEQokbnlvjzmUsC33zOCWbrhO5WqO3YwXfzJ+u4/x65acXFPCzLDctImhiAcBxmgPeF4/1QVcWKLkHVGbvkHop+rf0AjNkXSrlwmKurNfM4xmJt19G+yJDDbLQfAM8cZi+O67o6V32FBD+5Zmx1FkEQBADAnfNC3XzOCeb6etYXjY0OP5DCnd2xg10orcpqHrTFtpg+XSMGL1MyPCoDBhjEAIyJI8y0EoBj6OlJWjRiLClisHJvwxL906fzo6N94Vdaics4rO26vYg0csmF4LBfHP5mdnjjEAQhulz6QSibzTnBXFjIQtcLsWksDiZN0vzgWIwEs1KjXt6xg/8eNTUaG/aoDBjAMezYMWZYyUkh1IwqMwCe1MMGvBGbYTv9WjFMmMA5wAnHxMgI53Ib7YeiIp4r4ILJk/ni1e1xLU1LsoCFX+fHrnBOioIgRJB//nf8+cSZoQwh5wQzYCA2U7hp2uKgvZ0fwxDMQ0PA3r2jXrZiMKpf7JHYHBgAdu1ysHAKd9ZIbCrF+0LrSiE5RoLZixis9XiwH6ztOoqBKKnYdNXlr6bGdVpJfj5vO5QLYSFYPv6b+PM9wdZZFQQhovztq2GPQASzpydWjwVzSwvr4IykSWcwjiFosZliwlxTU7wesmN6e7kQt0f7AXAXgyvB7EEMVVX8N3STpmTs9Le3e+KSA+6P6+FhPqbGa0oGMT8holeIaB0RXZhkmQIi2pXQ2bUojPECAH4lszMFYdyjbHMbQpznIIK5qoqTTIeH9700OMh1nI3Fpke30a3b4BlJI9TCdskB9+6stkseVgwlJfzjpdj04MKFyL3YNM4lb2/3ZD8AHENDg8OFq6vjF04xpMsfPg/gAAAfBbAEwL8TUeK3ciaA/03o7DoQ9EBxmdMvqyAIOc/NtslkLu9WuiFnBXN7u8MmB5ZQs83qskpXGQmc0lLX+ZqAd2IzbJcccJf/G7bTX1bG1yNuxOaOHeyQa1WHGxnxzGEG3AtmY5fcY8HsZhKp8YVL7nAGuHmUUkp1AXgEwOkJy8wBMJmI/kpEL1idWgOnwvZFu3P/UIYgCELECKH2sp2cFcyAwxn1aU6sYYsDwFww9/ay9gxTbGpVLImoSw64z4k3unDp6mLRHKEYgHh5N8d4fEx0d/NPRrw8rrMMIjopIaViOREtB1ADwH7PqglAYuHMveCurGfEfq4mokNSbOcSIlpDRGtaW1uTLeKOxd/mx85N3q9bEITs4Omvx5+HUHvZTk4LZlOh5uoWekQEs3HTEktsejDZTKtiSWEhUF4eOZcc8MadjUIMWhVLkqRkaHf5AyJ5TOS6YFZKPZeQUrFUKbUUQAtGC+T62Gv2z76ilPqRUmpYKbUbwLMAFqXYzl2xTq+L6+rqvA/kZFvzkvV/8H79giBEn3V38uPkw8MdB0Qwey82PRIHtbWsIU3TGVzlnFZVaRagTo12PrltP/T08E8UxKbbCXNRiKG/n6tdZCRJmUKjGPr7uaZ3RASzdSE8jrv8PQbgKwBARGUAzgXwV/sCRHSslYZBRMUAlgJ4PdhhJuGpi8IegSAIQfPe4/HnX14X3jhiiGBOIjYbGrgUrfaJ1UPBnJenUUarspJzH2ziwJocFWZaCeAuFcBVDICnQk2rYoltPxh3+fMhBkDjrsvwMF+txGhoCLcuOQDMmMGPpoK5oYFTSsZxl79lAHYQ0RoAKwD8VCnVREQLieiPsWU2ADiXiF4Fp2bcpZRaH85wAVxruyWy6+3QhiEIQgj8+aywRzCKgrAH4AcTJ/IEK9MT6/btLA60TdawxGZeHgedEAMAzNSt7+1xDNOmAatWOVw4QWxaMcyapbnR9nZullFWpvnB5NgrlliiLSUJMRjXL/ZRMB+e6c6W/ZioqADA+yLj5xIJU/SnOK61j4ccQimlAHwnyevrAHw29rwdwPkBD80Z/33oaAEtCELu0vZO/HlEjvucdJi1ymglyWH+4APDE2vY7myCOKio0KxfDPgSg1bFEi9Fv0flZ7SFmjVhD9FyyQEzsdnfzw670YUL4FkMpaU8NNPjerwL5qzFXne1c3N44xAEITj+a37YIxhDTgpmQENsWq2AbakARifW3l6gr88XwWwyUcuKQVsz+iCYAYcVSxLyf7dvj1/8aOFTDI7FplJc2xsuXXJrfR5g1bI2SVOyPmN04QJ4vi8c1WJOmESqlAjmrMX+T+zO/cIbhyAIwdD6Vvz5NcOplwuYnBbMjk6sCa2AR0b4c1ERB3v2jCoRnZoUglmbsMVmQgxTpnB2hRYe1i8G3FVd+eAD/tVIMJeXGwSfnMJCYPJkM4fZldMPROKuy+7dnJItgjlLsZ80298NbxyCIPjP3Qvizyk6MjU6I/EYq4zWiJMuijZns7UVGBiIjjgANESOzSU3SivxuFkGoBnDpEmsagYHAUQnNaauTqNiibVdm2AuKmKxqoXHMQAaYjMHBbNxDEI0sJ80f3tQeOMQBMFftj4bfx5iG+xk5LRgHhpiAZwRL06sURDMsTH093MbYO0YPG6WAWjGYLWBjsURFZdcq2KJtd1Y/TZL9OfpHmk+CWZHd12SxAAYHhP5+Twh1SNMK5YYxyBEB/vJ8+0/pl5OEITs5aFT4s9DbIOdjJwVzNYtcOtEmZZJk0aJNPvnHeODYLbGYI0pLTU1LHCU2ieKohBDZSXrJUf7wRLMbW3uck7b2z3L/bWYOVM/BoA/o70fAF8E8+zZDmOoqOC8/lgM27fzULSLjlj7wcN/ejNm8DWd4y6e4jDnDvbv0ROfC28cgiD4w8p/jz+PSGUMOzkrmOfM4cdt2xwsXFs7ShwA0XCYZ8xgg27rVgcL19RwKkNPT6RiIGKh5jgGANi1C52dnL+tHcPAAKd1eCw258xx+F1KEMxRcckB3g+7d4/pej0WovgFGKIVg9ZxnSCY8/MNmhEJ0cJ+El12ZnjjEATBe/7xY34sj2Y71pwVzLNn86NjobZrFwA+sZaUsIbWwgexWVDAt6AdxWANuK0tUoIZMBObxk6/x80yLGbP5nSGjKkAtnSGoSFO44iKw6wlNhMEc9RicHRMJAhmo9rqQvTY/1P8+P4T4Y5DEATvuMl2B+kbTieqBEvOCuaqKk4HcCyYu7uBgQFs387OrvZd5I4OVrgTJhiMNjVz5ui7s5bYzNhkIxGfBLPlMGcsj5dEMEdJ9A8PO8gBLijgL15b275Jp9piUynfHGbATDBHxWG2/paOHea9e/cd15KOkSOcZ2uXe1O0chwFQTBgeDD+/Iz7whtHBnJWMAMGzmZ7u3tx4HGSuqk7W1NjmHMK+CI2u7ocpAJEXDADGik+u3aZl5Tbs4fTa8J0Z2Mx7NnD14JGx0RHh+e55CUlnFbh2GGOjUMEc47xhVfizzu3hDcOQRDcc6utfOqhF4Y3jgwYC2YiKiaibxHRSiJ6MMUyREQ/IaJXiGgdEQX6l9DOnW1ri0wpMwsrFWBwMMOCXsUAeC5y/n97Zx4nRXnt/e+ZhWEQFBj2RWAQZUcFcYkLkk2NxrxqojfGmBv9mGtM4oJRs783uXHJYnK91yya1bzGmJgoMS7RqOASo7KpIIswwyYMsss6wPC8f5wquqenl6qe6a7qnvP9fObTXdVPT53TT1X3r85znvMEjmx26wY1NYd8qKyEAQNCHqyAUXIIcT61J62kQD706aMfcZgIc7smyxXwmggjmA9u3sratXmmlRjxZNDUxPOf10dnh2EY7WPeTxLPr98ZnR0BaE+E+QCwBLgNyBRW/SQwCjgJOB34mogUbdqNH53NmQrg5f82r9vMO+9AfT7fvwUSB8OHJxZTyUqSYF65EkaMyONgHbxYhk/gyGbSZLPGRhVGoXNOCyQ2fbEVRjC3qxwbdLgPoSdgbt5MY4NePKHPp5YWHVIo0DURRjCvX76L5uY8rwkjviRPAPzdKdHZYRhG/jx9TeJ5l45Nae1o8hbMzrkW59xTwJ4szc4F7nHKe8BDwDn5HjMsw4ZpanLS4nHp8cTmqqV7cS5+ghkCRAW98l1u4yYaGkrUBzgk1NrlA3S4HzU1OmksjA8rV6oZ3buHPFiBfICQKT7799OwuBnIoy/8/JsC+bB6tWryrHiCuWHJPiDP88mIN6Mv1sd1L7fOgzQMI/4kz0GIYRm5VHIKZhGZLiKz0vwFGSyvA5qSttcDbdY8E5GrRGSOiMzZGGilkWAEFmqeYG54W3+B4yQ2A6cCVFVBz56sX3OAvXvj5YOfTx0mstkuwVxR0aGLZfiEjc6uWAEjR+ZxoAIK5rBpSg2Lm6mt1SXKQ1Fg0b9/P6xfn6OhL5hX6BexCeYy5PykBUx+0LEjY4ZhFJBVzyWeXz43OjtCkFMwO+eedc5NS/PXlOu9wAZaC+QB3r7UY9zjnJvinJvSt2/f4NbnIHAqgC8OVurHESexOXSoDqUHFTkNa6qBePkgEi6y+d67e9m0qR0+9OqVx9J6uQlVsWTHDlYsd7ETzMOHa/GLnblSxbxrYsVyR319HnNZC+wDBBx1ARpWVx1KRzHKkBl7E88fODM6OwzDCM4fpieeDzg+OjtCUOgqGTOBKwBEpBtwAfBEgY95iFCTzWpraXinhq5d85hotn+/5n4UQBx06aK1mIOKzYYmLY0RJ8EM4SKbjRs1hyFuPgwfriXWcqYC1NWxnypWrY5XWgmEuCb8m8jV+5N/4AAAIABJREFUlbHzIfCNsC+Y13dl6NAOT8034kJVDYw4S5+vngX7d0dqjmEYOSixVAyfDhfMIjJARGZ5m38G1onIHGA2cLtzLtdAaofRu7eu8tvQEKBxXR0rNvbIL5rm1as9NPGugxk+HBqDVE6qq6Nh8xGHIrqhKcCS0j4jRmg/BKnF3LBdP8e8hNqmTQUVzAcOBJuAuZojaWmR/CLMmzdr/bTa2jzenB1/4lvOa6JPHxzQsK5rfv3gXxMF6At/AmbOa6K6Gg47jIZ3e1g6RrnziaQ4zJ3xnjhkGJ2af92ReF4iqRg+7RbMzrlZzrlLkrabnHPTvOfOOTfDS7c4wTl3f3uPFwYRGDUK3n47QOO6Ohq29c5fpAF0YDpJMkcdFdCHPn1oeK9PftG0gwfVjwL5MGqULsvsf1QZqauj4aCGQfPuiwL6ALB8eY6GdXWsQJVyXoK5CD7kPJ/q6thIX3Y1V+fXD/5chAL4UVurEzBz9gNAr140butpgrkzcFPS0I8taGIY8eNgC8y+JbFdIqkYPmW9cAnA0UfDsmW527nedTTs7N8+wRx6Pe1gHH00rFunWR9ZqaujYe/A/HzYvl1zDQroAwToi7o6Gqin5+Et+QW7Cyg2fR+WLs3RsL2CeePGgvVD7976r3P2Q69eNKAnUt7XRGWlrnpYAI45JkA/ALuPGMj6Pb1MMHcGpAKm35nYXvZwdLYYhtGW71clnpdQKoZPpxDMK1dCc3P2dhu7j2DnwW7ti6YVSOQcc4w+BokKrjg4gvphuZJs01DAiCAkfAgqmOsH7c3RMA3OFVRsDhqkK58H9aGm6gCDBuVxoE2bCuYD6DWRU2xWVdHQbQLQDsHcp09BJl9C8Bvhxq5jAKvB3Gk44frE84cvCJADZhhGUUge9ZmRrRpxfCl7wXzMMZptkCtnc2nFmEPtQ1PglIygkc3t3QbSxEBGDdoV/iAFjpIPG6YppUGis0sYzdH93wt/kF279M6oQD6IBBRqXoS5vve2/PRiAaPkEFxsLqmZSIUcjF2UHPQ63bIld4rPkoqxh9obnYTkyNX3yv4nzjDiz4J7Es/PuA2qukZnSzso+2+ToGJz8f6jABhzzMHwB/F/tQs06W/kSBVruUTOkj2a+zum/5bwBymw6K+qUj9y+bC7Wx9WMYwxfd4Nf5AC+wABxWa3biyWsRxzeJDKi2kosNj0U3xylZZbzFjqa9dTU5PHQQos+n0BnPO6PqBJ26NHF8wUI45cn5S/ZvnMhhEd+3fD3z+X2D7plsxtY07ZC2Z/klMukbN451C6sYuhPbaFP8jGjZqrWV0d/r0BqK3VCG1OH7br+P+YXnkItQKnlUAwsbl0S18cFYzp8U74AxTJh8bG7Ck++/YLb7ujGNttZfgD7NsH771XcNEPuVN8Fu8fyZjqIDPr0lCEtBIIcE3sGc6RsprDrHBC56JLd3j/fye2n7omc1vDMApHctWaEsxbTqbsBfMRR+gqZTl/WLf25xiWUrF1c/iDFDiaBsHyThe/W0cXmqmvyUNsFik6u3x59jrGi9fpJLExXYPU0UuhwGklECzF5+23oYUqxlYFyHtIpQg+BBGbBw7Ast1DGOMW53eQAkfJhw8PluKzZMcgxri3NF3H6FxM+VLi+fyfwKa3orPFMDojyaM7N+Uxeh8zyl4wg4qcJUuyt1nc1JsxLA5Q9ywNBY6mQUIwZ5vDsvidHozibaq25eHDxo0ayu7WLX8jc3DMMRqZzbbgxOKlFVTQwiiC1NFLoUiiH7KfT4s9jTm25c3wByiCD0cdpSk+i7No4cZG2H+wijHNC8IfoKVFE4wL6IOf4pNNMB88CEs21ul1/W4eKT5G6ZMc0frlOHCl/6NtGCVBslj+9wV5LHARPzqFYJ4wAd54Q39A07FrF6zeWKs/rJvziDBv3FjwCPOECZpzmlVsNtTk70MRRP/Eifr4xhuZ2yxZAiOrV1Ozrc0K6rkpQkrG2LF63Wfz4a23QDjIMXvyEJtF8KG2VlOVsvngi+kxzfM1TSQMW7fqxVbg82ncOHgzyz3JmjWwe181o1mS+FyNzkerSYCV0dlhGJ2Fv3068XzqjdBvUnS2dCCdQjAfe6zWMM4kNt/yRurG8lZsxeaxx+rjggwabM8eaGisYGzV2/lFyYsg+seP1ypjr7+euc3ChTC2++r8I/1VVQWr/QtaVu7oozP3A8CiRTC8x2a6bY1nagzo+ZTNh4UL9XE0S8JfE0X0YcUKTflOh+/DOBaZYO7s3Jg06cAmARpG4VjxGCz6XWL7zO9HZ0sH02kEM2QWCHO91RmPZ154ceBcUQSzLzbnz0//+uuva1DvuJ6NsRX93bppWkamftixQ4fYj++7tn2pMQUe+jnuuOxic/58OHbQu9oPmYY1MlGEHGbQa6KxEbZlmOM6bx6M7L+TI3gvfF8UyYfjjtPHTDdg8+aBiGMSr1tKRmensgtcmZSDZKLZMDqe7SvhoXMT2yU+yS+VTiGYx43TRccyiZx586BXL8ewynfCR6J27YK9ewseTevWTUtj5RL9kweuyy+aVoQIM8CkSZl9eP11vf84fthm2JBnSkaBRRqo2Fy5Mr3Y3L5dJ/1NPmq7iuUtIUv8bdyogr937w6xNROTvBGyTGkZc+fC5LG7dSOs2CxCWgkkBHO2a+Looxw92GkRZgPqRsNH7ktsm2g2jI5j3074WdIKUWUmlqGTCOba2uyRzXnzYPJkQfr1DS8OihRNg+zD6HPnqt4dMtjlF00rQoQZ1IdVqzTNNZVDon/0LhU4+URni+QDpI9szpunj1Mm7tcnYYX/pk3Qq5emlhSQbKMuW7boDcHxniDN+5oo8A3YwIF6iEyjLvPmweQTKvQLwCLMBsD4y2DMJYntn+ezKo9hGK1wB+FHPRLbZSiWoZMIZoDJk+GVV9pWmWhu1olDxx2H1p+LsWA+/nidyLR+fdvX5s5VH2VA//AirblZ8yGKEGGePFkfX3217Wtz56oIGlhfq3XNMuULZKII5f0gEdlM58OcOfo4eao3uSif6GwRzqWBA2HAAL0mUvFF/+T3easx5SP6oeB+iOg14X/myWzcqNfK8cej54RFmA2fjz4ANT31+bYGeGB6tPYYRqmTPJm2DMrHZaLTCObTTlPtklp79rXXtAjA+96HCuaw4sD/IS6CUDvtNH184YXW+7duVdF/0klAv37qaLb6c6kUUfSffLIGT59/vu1rL7zg+dC/v+7Ipy+K4EO/fjpiMXt229defhnq66HPqF66I58bsCKcSyJw+unqQ+qp8sILmi9/wpndtbPyEf3du0PXwi9/euqpOrkvNfPFv0ZOOYXENWEYPtclDXGtfg4e/VR0thhGKZOc2nRjc1mUj8tEpxHMZ5yhj6kiZ9Ys7d/TTkN/WGMaTQONlnXv3taH559X0XPmmajY3LdPk2mDUkQfDjtMo8ypgnnlSv0780y0HyCcyPFr/xbBB9Dz6cUXWy/C0tICzz2X1A8QW9EPKpjfeadt9ZjnntNz7YheFflfE0XyYdo0PfdTz6dZszTvf8oULMJspCd52Pit++HvV0dni2GUIsli+brtOrm2jOk0gnnUKB2CnjWr9f7nntMJUL17k0jJyCc6W4SoYFWVRsLT+dC1K5x4IvmJzSJGyUHF5quvtl58zfdp2jTy82HLFu23Ivlw+ul6T5KcA7xggWaRTJ+OnlCVlbGNMEPiJvK55xL7du/WNI0zz/R25BOdLaLoP+EETVFO9gHg2Wc1+lxdjfpggtlIR7JoXvAz+Ntl0dliGKVEslj+0maoOTw6W4pEpxHMInD22fDYY5qyC1r1a/Zs+PCHvUb9+2vFix07gv/jd9/VX+XDi3OynHWW1o32U0ucg5kzVWjW1JBfZLNIVQ18zj5bg+CPP57Y98gjMHiwVjQ55EM+or9IPnzwg5q28PDDiX2PPqrn2fTp6It9Q04iLVKJQp9x42Do0NY+PPGE9s2hayJfwVwk0V9To+f+zJmJ+9zly7UW9iEf/H4IcyNsdB6SRfOi/we/OyU6Wwwj7jjXWixfuxVqC1vVKS50GsEM8IlP6CIHTz6p2w8/rMPoH/+41yCfyGZTk4aui5S3c9FF+vjgg/r42ms6pN7GhzCC2W87YEBHmJiT005TTez7sH279smFF6rOpK5OP88wPjQ16ePAgR1ubzr69dMo7IMP6veHc/DAAyreDn2MYdMZtm6F/fuL1g8iet489VSiaskf/6h63Y8+55XX718TReKSS7Tyyssv67Z/XvnXCv366Y1w8pBGJ0REakTkSyLyvIg8kKGNiMhtIvKKiCwQkUuLbWckJIvmdS/Djwq3+JFhlCwHmuF7SbLxum3QtWd09hSZTiWY3/9+1VM/+pEK5bvu0ijb8cd7DfKJzhZZHAwZohHMn/5Uh89//GPNa77gAq9BPtHZpiaNkvfq1eH2pqOyEi69VKPKDQ3ws59p1P/yy5Ma9OkT3gdI+F8ELrtMo5mPPaaCf9ky3XeIsNFZ34cink+f+pRGlH/yExWdf/mL7jtU1S7sJNKDB7V9EX342Mc0N/6uu1QX//SnejNz5JFeAz/aHTbaX34cAJYAtwGZ7vA/CYwCTgJOB74mIsW5C42aZNG87z2r02wYyex4B36YNJH7ht1Q07luLDuVYK6uhq98RdMwTj5ZK0t8/etJweF8orNNTUUVaQDf+paWljvjDI1qfvGL0NO/yfNXustH9BdxduuMGdClC5x7Lnz723DOOUk3LhC+xF+Ro+QAn/wkHHUUfO5zcOWVMGKE3ggcIqwPEQjm446D886D735X+6BLF7j++qQG/fvruus7dwb7h0WOkoNmQ113nUaWTz1VJzJ+/etJDXzBHCaPedQo+MIXOtTOqHHOtTjnngL2ZGl2LnCPU94DHgLOKYqBceBmBz2TajObaDYMWPsi/GRIYvumg1BdG509EdGpBDPA5z8PV1yhpahmzICLL056MZ/o7IYNRRUHoBPObr8dliyB88+Hb34z6cWqKk1pyCetpIgMGgS//72aOW4c3HtvSoOw6QxNTar2ehZveKi6WkVaTY0e+k9/0sdD5OMDFP0G7N57YcIEPfx99yVFZiF8mlIEoh/gG9/QlJ4lS+DWW708ch/fh6CC2TlYu1bLbJQgIjJdRGal+QvSKXVAU9L2eqBfhuNcJSJzRGTOxnKaVPm55TDxysS2iWajM/PSd+D+0xLbN7uyLh2XjcIuJxZDKivhF7/Qvzb4kaigIqelpejDzz4336x/aQmbd9rUpLO/iszHPqZ/aenXL/2KFJnwI/1FvpCPP17TStLSr5/mze7apTkDuYhIbPbvn34Bk0Mvgp7nIwOsihaR6K+pgYceyvBi2JSMbds0R6hI+fAdjXPuWeDZPN++gdYCeQCwKsNx7gHuAZgyZUp55bCcfS/UnwWPeInwdwjcuA8qq6O1yzCKyZ2Hwf7die0yXcEvKJ0uwpyV6motBxb0h3XzZhXNRRYHOQmbOxtBlDwn5eCDf14Ejb41NanyOyJGeWFh05QiEv1ZCTs3wV9KM04+FI+ZwBUAItINuAB4IlKLouKYC+HqNYntH3SBpnnR2WMYxeQOMbGcQt6COciMa6/d0pRhwSMztY0FYaKzcRQHEM6HCKPkWenfX0ua7N0brH0EaSU5CSs2fdEfp+GusGlKEeSS56S2VlN11q0L1r7IFVeiRkQGiMgsb/PPwDoRmQPMBm53zq2PzLioOXwIfPlAYvu3k2HmJdHZYxiFJrVs3MhzTSx7tCfCnHPGtYhUARucc9OS/la345iFJ4zYjKM4gHDR2U2btLJBHH2AcLmzcfMhrNiMow9h05SamnQVnSLVJQ/MoEHBBbMfYS5Tweycm+WcuyRpu8k5N8177pxzM5xzU5xzJzjn7o/M0LhQUdlaMCx50PKajfJkw/zWZeM+/gRc9Gh09sSMvAVzwBnXQ4GuIjJTRF4QkWvzPV7RCCM24xxhDhqdjbMPkLAvGy0tmvYQx9QYCCc249YP/kTKMD5EkEuek3wEc9z6woiWmx1UJ81FuEPAHYzOHsPoSO47EX6TVKrq+p2ax28cIqdgbueM6wp0WO9i4APAWSLy4dRGsZpt3b9/MJEGkU1wykkYsekLobj5MGiQPgYROXGNkvv2hEkFiFs/gEZa1wcclY+j6IfwPtTWxi9KbkTPDTvhvKSg+/cqYelforPHMDqCOwTWv5rYvtlBlwAT1TsZOQWzc+7ZlJQK/y+nGnPOrXDOfdk5t9c51ww8CkxN0+4ebwhwSt8iLambkUGDNDobZFWwpiYtPdW9e+HtCsPgwfr4zju528Y1wlwOPnTpolHmID4cOKBR8rj5ANoXQXyA+ApmP8IcZEGS9etVYMctSm7Eg7GfhBlJA6uPXGgpGkZpsq2x9bk76GTLV85CQatkiMhoEbnGe14BfAiI9zTjIV5x7iACIY6TtKA8xGa/flpTupR9gOBic+NGFXOl7APEs1oJqGDev18r2+Ri/fp4+mDEh6qubYXFHQIHAk5SNoyouXsw/Lw+sf3ZN+Cyf0ZnTwnQ4YI5ZcZ1IzBJROYCLwJznXOPdfQxOxRfbK5dm7vtunXx/GENI/rXr9cawXGLkldUaJQvqA8Qz74IKjZ9H+KYkjFkiNrX0pK93f798Y2S+xP4gqTHNDWV7YQ/o4O52cEH705s/7AWHv9sdPYYRi4OtujN3c6k78KbHfSdEJ1NJUK7BXOOGdfNzrmrnHOTnXOnOOe+097jFRxfbAYRzGvXRrLgR0569tQczKA+DBmSu10UBBWbvp/+zU6cGDw4WD/4fsaxLwYPTpQfzIaf8hBHH/yc+CB5zBZhNsJw/Odbl55789fehEAb2jZixjPXw/eT1qubeIWlYITAFi5JJWg6g798bhzFgUg4sRlHHyCcD337ajmzuDF4sE5KbG7O3m6Nt0BCHG/Ago66+K/H8XwKOol0zx5d6c9vbxhB8EvPHTEise97FfDcl6OzyTB83EG9iZvz48S+GXvg7HRLHhuZMMGcSrdu0KtXbnGwZYv+uMZRHIDaFURsrlkTT5EGwQXzmjXx7QdfbOYSamvXas52v37Z20VB0JvIOIv+oCkZcfbBiD//0QDXbk1sv/oDFSoHD2R+j2EUkofO1WouPl17681dVQwDTDHHBHM6ggi1OEfTIFgqwIEDOvwcZx927NC/bMQ1NQbCic3Bg6GyMnu7KAjqQ5yvia5d9UY4l2Be7a2rFNfzyYg/XXuqIKlJWuL++9Vwt41aGEVkzxa9WVuRNG3suu1wbYCJz0ZaTDCnY8iQ4MPPcf1hHTw4dxmt9eu1fnGcfYBgYjOOIg3Cic24+hC0YsmaNdCjBxxxRPZ2URFk8RKLMBsdxXXbdPEHn53rVcA0xbtQlFEG3CFwV11ie9j7vZs4qy3fHkwwp6McIsxDhsC+fZo/m4m4i34/jzRbX+zaBVu3xrcfwoj+uPZD0IolcRb9AEcemYggZ8IXzHH2wygduhymQuWEGYl9v51skwKNwvDsjLY1wW9qgUv+EY09ZYYJ5nQMGaL1ZPfty9xmzRodPo/rbPogE7XiLg6CiM24i36/Ykk2H+I8gdQnSE58nFNjAIYPh5Urs7dZs0ZL+9XUFMMio7Mw/QdtqxF8r8IWPDE6hk1v6bn02p2JfR9/Us85MZnXUdgnmY7Bg1XEZCtBtXatRt3imHMKwcrjxV1s+natWpW5Tdwj/SLqR7bIpl9FI679APr5+jdYmYhzagyoYN6yRVfyzMTq1fHuB6O0udnBNSlpQXeI1W428mPfLj1/fjkuse+IEXqe1X84OrvKFBPM6Rg2TB+zRaNKQRwANDZmbrNmjS5aEtec09pavSnJ5QPEuy/q67P7EHfRDzBihF4PBw+mf33/fl3wI84++Nd1thuwNWs0dcMwCkX3gSpozvlNYp9fu3ne3RnfZhiHcE7Plx+lLDh2s9NKLUZBMMGcjnpvuciGLCdeY6OKiLjSt6+K4Vw+DBsWv6W9k6mvz+1DRUW8RU4uH/wbM1/QxZH6ek1RyjRpbtUq/RKP8zXh30RmuhF2Lt655EZ5MeFyFTiDT0nse/oLKoQW3R+dXUZ88YXy91Kk2w27bAGSImCCOR3DhmmqxYoV6V/fv1+HbkeOLK5dYRBR+zL5APpanH2A3GJzxQoVOF26FM+msNTX68TErVvTv758uT7GuS982zKdT/5+/2YzjuQSzJs3w86diXaGUQw+9VJbsfO3T6kwWnhfNDYZ8SKTUL5quZ471d2isauTYYI5HdXVGrHMJA5WrdKlguMscCC72HROX4u7DyNGaMpCppXyVqyIt0iDhH2Z0jJWrIDevXWCYFzJNeriXytxPp/69dN6zJkE89tv6+OoUUUzyTAOcbNrK5wfu1yF0pOfi8YmI1oO7E0vlD/9mp4rvWL8fVuGmGDORDaxWQriANS+hob0eadNTbB7d/x9qK9XcZ9p0lypRMkh+/l01FHFsycfhg7VUZdsPnTtmlhRL46IZK+U4Uf6494XRnmTTji/fo8Kpx/Y6mydgvWvaX//sLb1/ive0nNj4JRo7OrkmGDORLZ0hlIRzPX1sHeviuNUSskHSC/UduyAjRvj74Of15tNbMbdB3/UJZsP9fWaTx5n6usTwjiV5cvVfkvJMOKAL5wHJImjlmYVUncINOdYAdUoPR6/Qvv2vqmt91+zTs+FPmOiscsAoCpqA2LLyJGa07h9e9sqEg0N8Y+mQUJsrliRWATEp9QEc7qbF1+8xd2Hww+Hurr0YtPPh7/00uLbFZZsoy6lkN4DMHo0PPOMplSlloRcvlxvCqwGsxEnLn9NH/91O8z+SmL/j71V206/FU7+Stv3GaXBgb1tI8k+N7VYHeUYYT2RCf/HP100atkyHbaNc3UJSAwtp/Ph7bdVMMQ9mjZwoFb7WLq07WvLluljKQyhjxoFS5a03d/YqOKtFHw46ij9zFNXKDt4UM+xUhDMY8ZoPny60nLLl1v+shFfTrpFo4xXp5y7z381Keqcpca4ES/+fnX6tIsBUxKjCyaWY4X1RibGjtXHt95q+9rChTB+fHHtyYcRIzQSvnBh29cWLVJxEOfqEqBD5OPGpfdh4UJ9ffTo4tsVlvHj1d5UsblokT6OG9f2PXFj/Hhd+CM1xaexEfbsKY1rwr+uFy9uvd85vaExwWzEncOPTBJUKaMkPz7CE2FWNSGWrH0xcXOz4GetX/vMfO1Tf0TBiB0mmDMxapQOzb7xRuv9O3eqQCgFgVNZqQLhzTfbvvbmm6UhcCAhNlNZuFCjmrUZhrPixPjxmuKzYUPr/W++qSMVY0ogN80/X1LPJ79vSuF88j/nVMG8erWuADhxYvFtMox8uemAiqzPpvxOHdiTEGa/nxaJaYbH1hWJvrj/tNav9RqVuPnpf2w09hmBMcGciaoqFZupgtmPOJeCOAAVAKk+7NqlOacTJkRjU1jGj4d339W/ZBYtKp1+8D/rVOG/cKHmBh92WPFtCksuwexHb+NMr17Qv39bwfz66/pogtkoRfpOSAivE29q/dqa2QnB9r8D245yGR3PymcSn/k9adLtrt+hfXXVsuLbZuSNCeZspBObvjgohQgzqFDbsEGrSfi89ZZ+aZaK2PTtTBabe/ZoHnap9EMmsfnmm6Vz49KnDwwY0Fb0v/mm5sL36BGJWaGZOBHmz2+9z7/OS+WaMIxMTLsjIZ4Hntj6tV1NWtPXF3NbTLB1GA9fkPhcH/xA29f/ozHRL126t33diD1WJSMbEyfCb3+rgrN/f933yitaNaMUJjhBImK2YAF88IP6/DUvR+q446KxKSzHekNVc+bA9On6fO5cnWw2pUTqUfbrp2Jz7tzEvu3bdTLjv/1bdHaFZdKk1j4AvPoqTJ4cjT35MHUq3H671iHv5uV6zp+v13SpiH7DCMKn/5V4/sjHYelDrV+/95jE8+pucN12qDBZEIjFD8JfL8ne5vPvQI9B2dsYJYNdGdk4+WR9fPFFuPBCff7Pf8JJJ8W/3qzP1Klq64svJgTzP/+p1SfiXiHDp29fOPpo9eEmb7jx5Zf10e+jUuDUU+GFFxLb//qXRvpPOSU6m8Jy6qnwzW/q5L/evXUCYGMjfOELUVsWnBNP1Mokc+fCaadpH7z4InzoQ1FbZhiF42N/Sjxf+UzbKOj+3fD96tb7rt0CXXsV3rZS4PlvwMv/lb1NZQ3M2BP/ClpGXphgzsaUKRqBmj1bBfO2bZo3e9FFUVsWnMMP10jy7Nm67Ry89JKKtFK6qE89FR5+WKPKFRXqw8iRGrktFU47DR56SCeYHXmk+lBRoTc1pcLppyfOofPO00corRuXE71h6pde0j5Ztkzz408/PVq7DKNYDH9/YjVB53ShjKY5bdv9d+/W2wMmw6dehsrqtm3LiYYn4U9nB2t75WKoK4FKTUa7McGcjepqeN/74Omn9UvlySf1sdQiUWecAXffrVUA1q7VpYFvuinn22LFGWfAr36lUcEJE+Af/4DLLovaqnCccYY+Pv00XHEFPP44nHCC3tSUClOnavWYp59Wwfz445qiVCqpMaA3WccdB48+CrfcAk89pfv9/jGMzoRI61JmzsFD50LD423bNs2FH6QpRTr1y5o7XUpBGIB334BfTwr3ns/Mt4oWnZR2CWYR+S5wJlAN/NU5952U17sAPwXGAF2Bm5xz/2jPMYvOBRfA1VdrDvCDD+qPbSlFBEEj4nfeqRHaxkbd99GPRmtTWM47T29gHnhARf+uXaXnw8SJuvjH738P06ap+L/ttqitCkfXrvCRj8Af/wi33gozZ8LZZ2vflBLnnw//+Z96Lv3hD3oTdvTRUVtlGNEjAh9/rPW+rSvSV3vwefX7+peJaXfA5C9BVdeOsTEo616Fxz8DmxfnbJqW8ZfDOb8uvRsBoyCIy7PEjIh8BLiUDjcSAAANa0lEQVTAOXeFiFQCLwFXOefeSGrzNaC3c26GiAwGZgHjnXPNmf7vlClT3Jw5aYaGomLLFhg6VEt/LVqkEalbb43aqnA4pyW/du2CHTs0av63v0VtVXguvhgee0wnYLa06MpsVSU2SHLrrfC1r6l4XrJEo/1xX2I9lb/9TW9gJk3ScmzPPgtnnhm1VeFYuVJrrfulI++8E66/vkP+tYjMdc6VUMi9/cTue9soPAcPwBNXwML7orakY/jk8zD0tNztjLIj6Hd23oLZO0iNc67ZE8wvA59yzi1Lev1l4HJ/n4jcB/zWOfdMyv+5CrgK4Mgjj5y8Kt2ytVFy9906qWnkSK0I0Lt37vfEjX/8QyODtbU6wakUy2etWKG5slu2wJ//rFHCUmPXLs2hXbQIvvtd+OpXo7YoPM7pyMsjj+hNzAMPlGYE5lvfgm9/W9MzXnqpwxbAMcFsdHr274HnboT5P4nakgTVh8HHHoL6s6K2xIgZHSaYRWQ68M00L13inGvyIsf3AA87536R8t5lwBTn3Hve9h3AAufcA5mOF9sv3jVrtA5tKawql4l339WlsHv2jNqS/NmxQ0XngAFRW5I/zc1aXWLYsKgtyZ+DBzW9Z8SI0qkYk46VK2HQoA5dIt4Es2GEZP9uWD0bVj0DG+bB9pWwdyvs2wGuJdGutg76jNOFWvqMh4FTod9EK4VntIug39k5zzLn3LPAsxkOMg24EbjBObc0TZMNQD/gPW97gLev9Bg6NGoL2k8pVZTIRI8epV8rt6amtMUyqEgulVrk2SiV0oqGUc5Ud4ORZ+ufYcSUvENDIjIauAHNY04nlgFmAld67fsDJ6G5zoZhGIZhGIZRErRnHONKYCTwlCTyF+8EVgO3OOcuAe4CfikirwACXJNtwp9hGIZhGIZhxI28BbNz7kY0HSMdl3ht9gElVizXMAyj/BCRGuBzwEXAO865tGuyi8hSYH3Srk8751YXwUTDMIzYYpnyhmEYnYMDwBLgNuDydA1EpArY4JybVkS7DMMwYk8JT283DMMwguKca3HOPQXsydJsKNBVRGaKyAsicm2RzDMMw4g1FmE2DMMoI3KVAs3x9gpgNvANwAGPiMgS59zf0xwnuX5++4w2DMOIOSaYDcMwyohspUADvHcF8GV/W0QeBaYCbQSzc+4etAY/U6ZMyX8FLMMwjBLAUjIMwzAMQMuFisg13vMK4EPAvGitMgzDiB4TzIZhGJ0YERkgIrO8zUZgkojMBV4E5jrnHovMOMMwjJhgKRmGYRidCOfcLGBW0nYTMM173oyXl2wYhmEkEOfilXomIhuBVXm8tQ+wqYPNiRPl7J/5VrqUs3/5+jbMOde3o42JM3l+b8fp3DFb2hIXOyA+tsTFDjBb0lHQ7+zYCeZ8EZE5zrkpUdtRKMrZP/OtdCln/8rZtzgQp8/XbImvHRAfW+JiB5gtUdhhOcyGYRiGYRiGkQUTzIZhGIZhGIaRhXISzPdEbUCBKWf/zLfSpZz9K2ff4kCcPl+zpS1xsQPiY0tc7ACzJR0FtaNscpgNwzAMwzAMoxCUU4TZMAzDMAzDMDqcshDMIvIJEXlVROaKyA+jtqc9iMhFIvJHEVmdtO9IEXlSRP4pIrNEZFiUNrYHr69eFpEXPD+7icgkEZktIv8SkUdFpFfUduaDiNzk9dE8EfmViHQpp77zEZFv+AtdlFHf/dbzYZb399Fy7LuoEZHvep/nayLyjTSvdxGRXyZdRx8okB01IvIlEXleRB7I0m5p0jkxS0SOLLYdotwmIq+IyAIRubQjbQhzHBGpEpFNKZ9Jlw60IetvufdZvebZd2NHHTcPO2al/E0tkB1t9EAYO4tsS5vv0ALa0kZHpLxemPPEOVfSf8AwYClwBCDAg8CFUdvVDn/OQGsJNiXtexo4z3t+DvBo1Hbm6VtvYA5Q621/H7gWWAxM8vZ9HvifqG3Nw7c+wHdJpDn9Afh4ufRdkp9TgF+hC19IOfSdZ/uz/nmZtK+s+i7qP+AjwC+955XAv4CJKW2+BvzQez4YeBuoKYAtleiy32cDf8jQpgp4vsCfSRA7LgUe8q63w4G3gIEFsCXncYARwO8L9Flk/S0H3ge8DHTx/l4EphTbDq/Ny4U8L5KO00YPhLGzWLZ4r7f5Di2QHel0xJeKcZ6UQ4T5LODPzrntTj+tnwMfi9imvHHOzXbOHSq87d05jXbOPeq9/jgwviPv6ouFc24LcKpzbo+3qwrYC2x1zr3u7fsF+sNaUjjnNjnnvuaccyLSHf0Se4sy6TsAEakFfgzc4u06mjLoO4+ewE+9SN//ltN1FxecLrH9+aRdFej1n8y56Hc4zrl30B++UwtgS4tz7ilgT5ZmQ4GuIjLTi2RdG5Ed5wL3OOU9VNSe09G2BDzOcKCfiDzhfSaXdODxc/2Wnwv82jm3zzm3D71xP78Djx/IDhGpAo7wIpvPi8h3RKSyAHa00QNh7CyyLZD+O7QQdqTTEcnXT8HOk3IQzHVAU9L2eqBfRLYUgp7AxpR976J+lxzOub0i0lVE/huoBRaS1H/eCV6yS7aLyP1AI/AMsI0y6jv0Tv7Hzrl3ve1W116J990c4BvOudPRPrub8uq7oiEi09MMWc8SkQHOuWYRGQz8FRVny1Le3qHf59lsCfD2CmA2cDHwAeAsEflwBHYU5TMJeJzd6OjSud7fl0VkbL62pJDr+MX6rc91nO7oeXEVuqT8QODKAtiRi7hpn9Tv0DYpVx1FGh3xq6SXC/a5lOqPWzIb0GEinwHevnJhE21/pPsSj2UoQyMiQ4B7gbucc0+IyEiSTmYRqQH2RWVfe3HOXerdWf8OeI8y6TtPKPRyzj2UtHsDZdJ3zrmrkjb/hArmsui7YuOcexYdnm2DiEwDbgRucM4tTdPEP6fe87bb9X2ezZYA710BfNnfFpFHganA34tpBynXGfqZhF2GPKctIvK7XMdxzr0CvOJtbheRZ4DJ6Ghae8n1W57ucyjEb31WO5xz24Cr/W0R+QtwId7ISBGJlfZJ8x36P4U6VqqOSHm5YOdJOUSYHwf+j4j08LY/C8yM0J4OxYvavSkiZwGIToJZ5JzbH61l4RGRrsBvgKv8k9z7UeouIuO9ZpcBqRdA7BGRY0XkcgDn3G5gGdCNMuk7NJrUV0QeEZFHgPHAtyiPvqv1hlX9dIuz0WhJufRdLBCR0cANwAUZxDLod/eVXvv+wEnAS8WxsDUiMlpErvGeV6C5xvMiMGUmcIVnRzfgAgpzneU8joi8z0/D8G6QpwHzO+j4uX7LZwKfFpFqLwXicnSkoqPJaoeIDBCRr4qIeLvOIprzIjbaJ8N3aEE+k3Q6IoWCnSclH2F2zq0XkVuB50VkH/CCc+7PUdvVwVwD/EZ0Vnkz8O8R25MvHwDGAL9LfNfwLPAZ4F4ROQhsRk/wUmMpcLWIfBHNp1oLfAd4mDLoO+fcF5O3RWSWc+7TInIsJd53zrk9IrIJeFVEtgPvAJ9DJ5eUfN/FiCuBkcBTSdf/ncBq4Bbn3CXAXcAvReQVdCLTNc655mIZ6KVI/ME5Nw1NrZokInPR/n/Cy8Muth1/Bk4WkTmAA253zq0vwGHTHse7xv3+WQxcKyIzgANoWs3Cjjh4pt9yL13kEufcHBH5KxrhbkE/nzkdcewwdqDRyu7APBHZCSygiAt3iMgf0L5ZELX2SbEl3XdoIcikI6ZT4PPEFi4xDMMwDMMwjCyUQ0qGYRiGYRiGYRQME8yGYRiGYRiGkQUTzIZhGIZhGIaRBRPMhmEYhmEYhpEFE8yGYRiGYRiGkQUTzIZhGIZhGIaRBRPMhmEYhmEYhpEFE8xGp0FEhojIxVHbYRiGYRhGaWGC2ehMvB84PmojDMMwjNx4Sy7P9pY4bhX0EJEuIvK8iJT8isVGaWCC2egUiMip6DK8F4nIAhEZEbVNhmEYRlY+C/zFOdfibR8Kejjn9gHPADZqaBQFE8xGp8A59yLwGnC+c+5Y51xj1DYZhmEYICLPicgHvef/JSJ3eS9dCsz09qcLejzitTGMgiPOuahtMIyiICKNwNHOuf1R22IYhmEoInI68G3gXuCTwEeBSmC1c25AUrsngRudcwu97UqgyTnXt/hWG50NizAbnQIRqQO2m1g2DMOIF8655wEBbgAu8VIw+gDbUpoeAyxNel8LsE9EehTLVqPzYoLZ6CyMANZFbYRhGIbRGhGZAAwEmp1zO7zde4CuSW0yBT1qgL1FMdTo1JhgNjoLS4A+IrJQRE6J2hjDMAwDRGQgcD9wPrBLRD4M4JzbClSKiC+a2wQ9PBG90UYOjWJggtnoFDjndjrnpjrnxjvn/hm1PYZhGJ0dEekG/AWY4ZxbDHwH+L9JTZ4CTvWepwt6nAk8XiRzjU6OTfozDMMwDCN2iMhxwA3OucsyvP4X4CvOuaXpXjeMjsQizIZhGIZhxA7n3HzgOX/hkmREpAvwiIllo1hYhNkwDMMwDMMwsmARZsMwDMMwDMPIgglmwzAMwzAMw8iCCWbDMAzDMAzDyIIJZsMwDMMwDMPIgglmwzAMwzAMw8iCCWbDMAzDMAzDyML/B/jk3kJbDm2rAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"import numpy as np\n",
"from scipy.integrate import odeint\n",
"\n",
"def plot_func(t,x):\n",
" fig = plt.figure(figsize=(12,5))\n",
" axes = fig.add_subplot(1,2,1)\n",
" axes.plot(t, x[:,0], 'r', label=\"$x(t)$\")\n",
" axes.plot(t, x[:,1], 'b', label=\"$v(t)$\")\n",
" axes.set_xlabel(\"$t$\")\n",
" \n",
" plt.legend(loc='upper left')\n",
" #plot a trajectory\n",
" axes = fig.add_subplot(1,2,2)\n",
" axes.plot(x[:,0], x[:,1],'#ff8800')\n",
" axes.set_xlabel(\"$x(t)$\")\n",
" axes.set_ylabel(\"$v(t)$\")\n",
" plt.show()\n",
"\n",
"dt = 0.01\n",
"n_steps = 5000\n",
"t = np.arange(0, n_steps*dt, dt)\n",
"x = np.zeros((2))\n",
"x[0] = 2.0 # initial position\n",
"x[1] = 0.0 # initial velocity\n",
"y = odeint(harmonic_eq,(x[0], x[1]),t) # The definition of the differential equation (1st argument) must be defined in the above.\n",
"plot_func(t,y)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"## Exercise 1\n",
"\n",
" - Read the above scripts and examine how the values of the time step \"dt\" and the parameter \"k\" affect the result.\n",
" - Try to solve the following differential equation by the Euler method and other improved methods mensioned below. (It is recommended to try it on a new notebook.)\n",
" $$\n",
" \\begin{eqnarray*}\n",
" \\frac{dy}{dt} & = & z \\\\\n",
" \\frac{dz}{dt} & = & \\mu (1-y^2)z -y\n",
" \\end{eqnarray*}\n",
" $$\n",
" The solution for $\\mu > 0$ would show pretty interesting behavior. (This is called \"van der Pol equation\".)"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"## Appendix: a simple example to add inline GUI\n",
"\n",
"\n",
"You can easily make a graphical user interface for choosing parameter values by [ipywidgets](http://ipywidgets.readthedocs.io/en/latest/examples/Using%20Interact.html).\n",
"A simple implementation is shown below.\n",
"\n",
"Unfortunately you cannnot change the width of the internal description field, and so the string representation of the slider value is limited as seen at \"dt\".\n",
"\n",
"The function in \"interact\" is always updated when the state of widgets is changed. This feature is incovinient if it takes long time to execute the function. For such cases, try to use \"interact_manual\" instead of \"interact\". A button is automatically added to the interact controls that allows you to trigger an execute event.\n",
"\n",
"More flexible gui examples are written in http://toyoki-lab.ee.yamanashi.ac.jp/~toyoki/lectures/simulationMethods/ipywidgetsExamples.html\n",
"\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"data": {
"application/vnd.jupyter.widget-view+json": {
"model_id": "bb50978facbf42e7ada34cc2ead65dc4",
"version_major": 2,
"version_minor": 0
},
"text/plain": [
"interactive(children=(Dropdown(description='method', options={'Euler': …"
]
},
"metadata": {},
"output_type": "display_data"
},
{
"data": {
"text/plain": [
""
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"from ipywidgets import interact, fixed, interact_manual\n",
"interact_manual(calc_plot2var, method={\"Euler\": euler_2var,\n",
" \"Heun\":heun_2var},\\\n",
" equation=fixed(harmonic_eq),\\\n",
" dt=(0.001, 0.05,0.001), n_steps=(100,10000,100))"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.11"
},
"latex_envs": {
"bibliofile": "biblio.bib",
"cite_by": "apalike",
"current_citInitial": 1,
"eqLabelWithNumbers": true,
"eqNumInitial": 0
},
"toc": {
"base_numbering": 1,
"nav_menu": {
"height": "227px",
"width": "252px"
},
"number_sections": true,
"sideBar": true,
"skip_h1_title": false,
"title_cell": "Table of Contents",
"title_sidebar": "Contents",
"toc_cell": true,
"toc_position": {
"height": "394px",
"left": "6px",
"right": "698.295px",
"top": "124px",
"width": "165px"
},
"toc_section_display": true,
"toc_window_display": true
}
},
"nbformat": 4,
"nbformat_minor": 1
}