非線形方程式の数値解法

テキスト

プリントテキストは配布しますが、e-Learningのページ

https://moodle.yamanashi.ac.jp/2016/course/view.php?id=5288

からも入手できます。（若干の変更があるかもしれません。変更があれば再度アップロードします。）

補足

プログラム4.2に相当するscilabプログラム

// プログラム４．２相当 ///////////////
deff('y=func(x)','y=x-cos(x)'); // 関数定義
deff('yp=diff_func(x)','yp=1.0+sin(x)');  // 関数の微分

[x,v,info] = fsolve(1, func, diff_func) //引数　初期値、関数のみ

mprintf("解は%f、残差は%fと計算されました。", x, v)

fsolveは，ニュートン法ではなく，別の高度な方法（「修正パウエル混合法」）を用いており，４．２の関数のような場合は，「関数の微分」を与えなくても解ける．

// プログラム４．２相当 (関数微分なし）///////////////
deff('y=func(x)','y=x-cos(x)'); // 関数定義
[x,v,info] = fsolve(1, func) //引数　初期値、関数、関数の微分

mprintf("解は%f、残差は%fと計算されました。", x, v)

またfsolveは，多変数の連立非線形方程式に用いることができる．

matlabには同様な機能を持つ関数としてfzeroがある。 matlabのスクリプト例

%関数定義（無名関数）
f=@(x)x-cos(x);
%非線形方程式の解： f(x) = 0 を満たすxを求める
z=fzero(f,2); %初期値を第2引数としてわたす
disp(z);

ニュートン法をグラフィカルに理解する

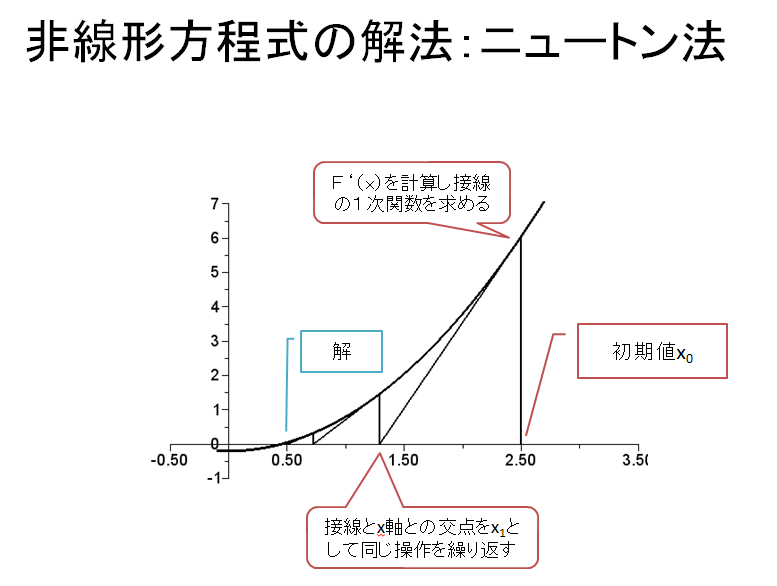
プリントテキストの図作成に用いたscilabプログラム（スクリプト）を課題１用に直したファイルを下に掲載する。scilabについては、参考として触れるのみだが、時間に余裕があれば実行して、ニュートン法の動作を確かめてみて欲しい。

次のプログラムを、".sce"という拡張子をつけてセーブし、scilabで開けば実行できる。

///////////////////////////////
// ニュートン法での非線形方程式の解をグラフィカルに理解する
// （計算誤差にも留意）
///////////////////////////////
clf()
funcprot(0)
// 定義 //////////////////////////////////////////////
deff('y=func(x)','y=x-cos(x)'); // 関数定義
deff('yp=difffunc(x)','yp=1.0+sin(x)');  // 関数の微分
x_start = 3.0 // ニュートン法の初期値
//////////////////////////////////////////////////////
x_max = x_start*0.9; x_min= x_start*1.1;   //描画範囲をニュートン法の計算結果に基づいて決めるための記憶
y_max = -1000; y_min = 1000;

// ニュートン法
x0= x_start
for(i=1:30)
    if x0 < x_min then   // 関数描画のための座標範囲　記憶
        x_min = x0
    end
    if  x0 > x_max then
        x_max = x0
    end
    if func(x0) < y_min then
        y_min = func(x0)
    end
    if func(x0) > y_max then
        y_max = func(x0)
    end

    //ニュートン法の解への接近軌跡の描画
    x1 = x0-func(x0)/difffunc(x0);
    plot([x0 x0],[0 func(x0)],"b-", "thickness",2);
    plot([x1 x0],[0 func(x0)],"b-","thickness",2);

    x0=x1;
    disp(string(i)+"回目: "+string(x0))
end

x_min = x_min -1.0
x_max = x_max*1.1
x = [x_min: (x_max - x_min)/100:x_max] // 最小値は必要に応じて変更
plot(x, func(x),"r-", "thickness",2);  //関数の描画

ax = gca()
ax.x_location = "origin" // 軸の位置指定
ax.y_location = "origin"
ax.box = "off"

縮小写像の方法についての参考図

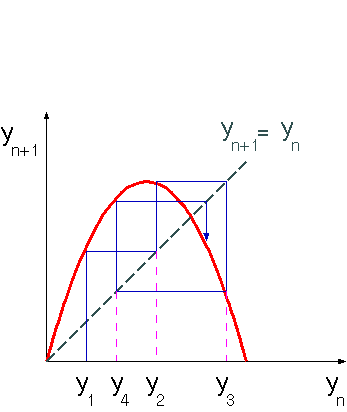
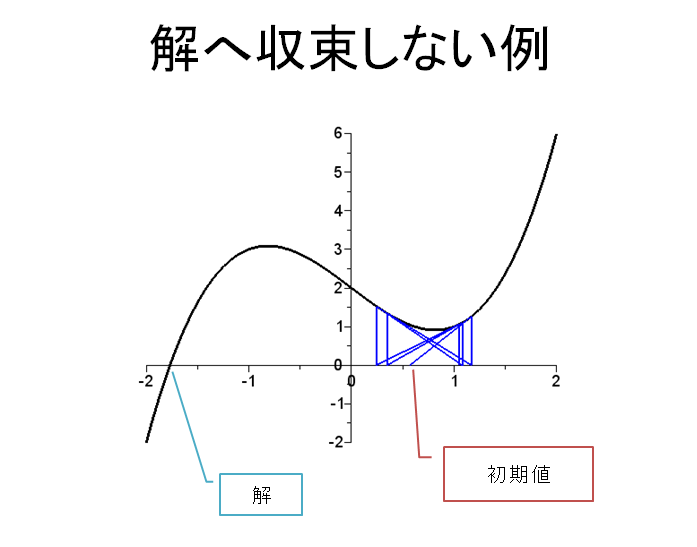
ニュートン法の繰り返しにより得られる数値解の変化を、y_1, y_2,...として次のような図をつくると、解が収束するばあいは、一点に軌道が巻き付く。