Laplace方程式の数値解

参考書：「計算物理学入門」（ハーベイ・ゴールド／ジャン・トボチニク著，ピアソン・エデュケーション）

複雑な境界条件を満たすラプラス方程式の解を「緩和法」を用いて数値計算してみる．

配布テキストはこちら

シンプルな「緩和法」

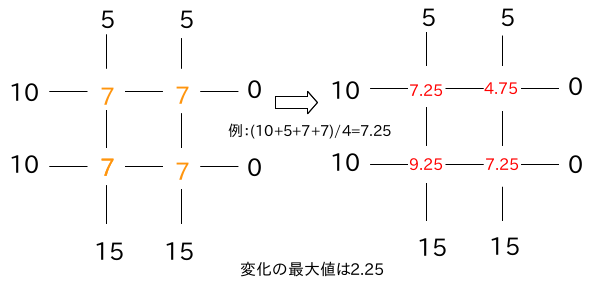
仮の値から出発して，各格子点の値を計算・更新を繰り返し，更新しても値が変化しなくなったら，それが求めたい場の値であるとする．

初期パラメータの設定
- 境界条件をセットする．
- 平衡への到達を判定する基準値pをセットする．
各格子点に初期値（仮の値）を置く．
最近接の４点の値の平均を，新しい値とする．すべての格子点について新しい値を計算する．
- すべての格子点の新旧の値の差の最大値αを記憶しておく．
αがpより小さければ，平衡に達した判断する．

課題5-1

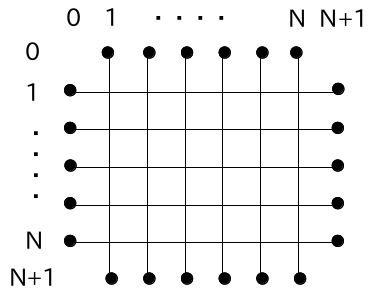
図のような，N=100程度にとった正方形の系について，左辺の境界を5V，右辺の境界を10V，下辺と上辺の境界を15Vの電位に固定した時の内部の各格子点の電位を緩和法により求めなさい．平衡値への到達条件はいくつか設定して試してみなさい．その他の境界条件も試してみましょう。

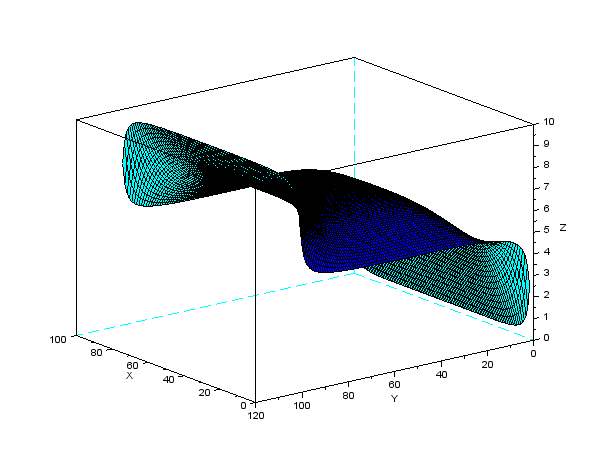
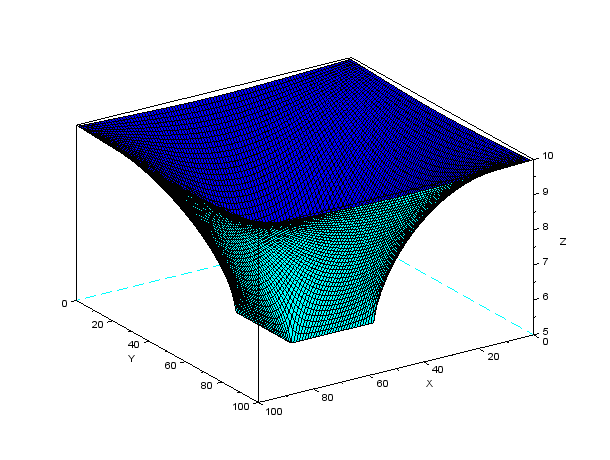
結果の描画例 (x=0とx=N+1では5V，y=0で0V，y=N+1で10Vの場合)

課題５-2

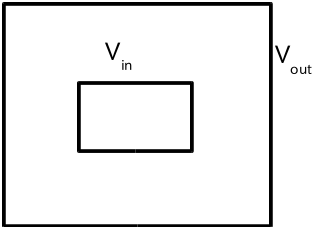
図のような同軸の正方形角筒の断面における電位分布を求めましょう．内側の境界の電位V_{in}と外側境界の電位V_{out}を与えて，内部の電位分布を緩和法を用いて求めなさい．内側境界の大きさは各自設定しなさい．

外側の境界がアース線，内側境界が芯線にあたります．ここでは，内側境界の内部は中空であるとして，内側の電位も緩和法により計算しなさい．（つまり電位が固定されているのは境界上のみとします．内側境界の内部は空っぽとします．）

（注）実際に用いられる丸い同軸ケーブルの形の場合は，電磁気学で学んだように，解析的に求められる．（復習しておくこと）

数値計算結果の図示について

電位の分布をcsv形式(Comma-Separated Values) のファイルに格納し，scilabあるいはmatlabを用いて図示してみましょう．

csvファイルは、各点での値をカンマで区切ったデータ例：

2.510621,3.509451,3.984702, ...., 6.508007,7.498126
1.532948,2.542317,3.179638, ...., 7.492532,8.484510
....
2.510621,3.509451,3.984702, ...., 6.508007,7.498126

scilabとmatlabでは，鳥瞰図をつくる関数が異なります．前者はplot3d, 後者はsurfです．以下にプログラム例を示します．

scilabの場合

  chdir('U:\My Documents\Visual Studio 2010\Projects\prog3'); // カレントディレクトリを変更(各自の設定)
  z_val = csvRead('e_field.csv') // csvファイル名(各自の設定)
  lx = size(z_val,'r');          // １辺の長さ
  ly = size(z_val,'c');
  x = 1:lx;  y = 1:ly;
  plot3d(x,y,z_val(1:lx,1:ly));

scilabの立ち上げはスタートメニューから行ってください。

matlabの場合

  chdir('U:\My Documents\Visual Studio 2010\Projects\prog3');  % カレントディレクトリ
  z_val = csvread('e_field.csv'); % csvファイル名(各自の設定)
  mesh(z_val);                    % surf関数を利用してもよい

マウスドラグにより，いろいろな角度から眺めてみよう．scilabでは，マウス右ボタンを押下しドラグ，matlabでは，視点移動のメニューボタンを選択し，左ボタンを押下しながらドラグする．

matlabで鳥瞰図を回転させるボタン(右ボタンドラッグで回転できる)

pythonスクリプトによる図示

pythonの実習はしませんが、興味あれば使ってみてください。スクリプト例だけ示します。

# -*- coding: utf-8 -*
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

data = np.loadtxt("e_field.csv",delimiter=",")
x = np.arange(0.0, data.shape[0])
y = np.arange(0.0, data.shape[1])

fig = plt.figure()
ax = Axes3D(fig)
X, Y = np.meshgrid(x, y)
ax.plot_surface(X, Y, data, cmap=plt.cm.hot) # X, Yはdataに対応する２次元配列
#ax.contourf(X, Y, data,  zdir='z', offset=-2, cmap=plt.cm.hot) # 等高線図

plt.show()

gnuplotを用いた図示

オープンソースのgnuplotを用いると、Cプログラムから呼び出して使うことができるので、上記のように、別途、ソフトを立ちあげなくても描画できます。

Cプログラムから直接gnuplotを呼び出す

Cプログラムで、電位に対する２次元配列を次のような関数を利用すると、gnuplotにデータを直接渡して（パイプと言います）、描画できます。 (教室端末のLinuxにはgnuplotが入っていますので、これが可能ですが、Windowsで可能かどうか、調査中です。）

void outResult(double v[][N+2], int n) {  // (注)
  int i, j;
  // 結果出力
  FILE *FP;
  FP = popen("gnuplot -persist","w");
  fprintf(FP, "splot '-' matrix with pm3d\n"); // matrixオプション
  for(i=1; i<= n; i++) {
    for(j=1; j<= n; j++) {
       fprintf(FP,"%f ", v[i][j]); // データは空白区切り
    }
    fprintf(FP,"\n");
  }
  pclose(FP);
}

（注）正方形の場合は、上記のように配列の大きさはnだけ与えればいいですが、縦横の長さが異なる場合は、それぞれを引数にしなければなりません。

データをファイルから読み込んで表示させる場合

Windowsのスタートボタンからgnuplotを立ち上げます。
「ファイル」→「ディレクトリの移動」メニューで、csvファイルがあるディレクトリに移動します。
以下のようなプログラムで描画できます。
- gnuplotでのデータ区切りは空白なので、カンマに切り替えるには下のようにsetコマンドを実行します。
- データ形式をmatrixとします。(gnuplot標準ではx,y,zの値を１行ずつ入力し、最後に"e"を入力する方式になっています。)

set datafile separator ","
splot "e_field.csv" matrix with pm3d

TOYOKI Hiroyasu
Updated: 2017-01-04

Home / Prog3Home