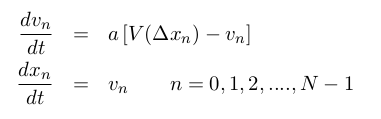
高速道路において、事故や車線規制がなくてもある程度以上混んだ状況の元で渋滞が発生することを目にしたことがあると思います。このような渋滞を自然渋滞といいます。等間隔で走行する状態が不安定になり、直線的な道路のなかに混んだところ(渋滞クラスター)と空いたところがまだらに分布している状況が出現するのです。(このページの下に実験のビデオがあります。参考にしてください。)
このような道路の自然渋滞を説明する一数理モデルを例に,モデル方程式のたて方,数値シミュレーションプログラムの作り方を実習します.
n変数の微分方程式である以下のような「最適速度モデル」の数値計算と視覚化プログラムを実習します。モデルについての解説は、配布テキストを使って行います。
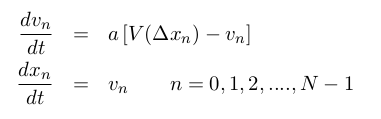
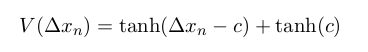
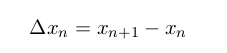
授業の進行状況に応じて、以下にコメントを付け加えていきます。
完成に近づいている人も何人かいますが、関数funcの構成に問題があるか、どう書いていいかわからない人もいます。参考として例を示します。
funcには、変数(位置、速度)xを入力とし、微分方程式の右辺の値を計算しxoutに代入する命令を書きます。N台の車全部の位置、速度について計算する必要があります!
台数Nは定数宣言されているので、下記を同じソースファイルに入れていればOKですが、分割コンパイルする場合はfuncの引数に入れるなど関数内で利用できるようにしなければなりません。
void func(double *x, double *funcVal) { // 速度と位置xを入力にし、微分方程式の右辺の値をfuncValに代入する long i; double headway; // 前の車との距離Δx for(i = 0; i < N; i++) { headway = x[i+1] - x[i]; // 微分方程式のΔxに対応 // 周期的境界条件のために、headway<0になることがあるので、その場合はLを加える1行を書く funcVal[i] = ; // 微分方程式の右辺(i台目の位置) プリントの(4)式 funcVal[N+1+i] = ; // 微分方程式の右辺(i台目の速度) (3)式 } funcVal[N] = funcVal[0]// ゼロ台目の車の位置変化をN台目にコピー }
時間発展の繰り返し箇所の書き方がどうしてもわからない人は、こちらを見てください。(画像として貼り付けてあるので、参考にして手打ちしてください。)
オイラー法,ルンゲクッタ法の関数として,課題3ー4の解答例中「発展課題としたプログラム例」での定義を前提にしています。
部分渋滞が起こるのは、a<2かつ中間的な混雑度(車密度)の場合です。c=2とした場合の部分渋滞発生領域は次のようです。図を参考にaとLを変えてシミュレーションし比較してみてください。
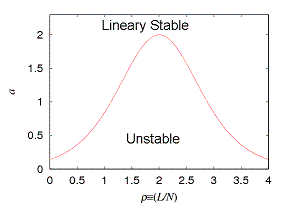
課題4−1ができたら、課題4−2に取り組んでください。
cpgsci(3); cpgcirc(x_draw[n], y_draw[n], 0.01);
どのように車(●)を書いたらよいか、ノートにイメージを描いてみましょう。構想ができてからプログラムにとりかかってください。
作成するプログラムのイメージをつかむために,ブラウザ内で動作させる動作例(JavaScriptで作成)を下に掲載する.(注:感度パラメータaが V'(L/N)<a/2 では渋滞が発生,以上では起こらないことが,解析的にわかっている.下のシミュレーションでは a=2 が境目である.)