サポートベクトル識別機ノート

最大マージン分類機

２クラス問題を考える。

説明変数$\boldsymbol{x}_i$に対して目標（目的）変数$y_i$がデータとして存在するとする。学習データの集合$\{(y_i,\boldsymbol{x}_i)\}$、 $i=1,\cdots ,N$を識別することを考える。（図はWikipediaより)

SVMは、原初的には、多次元空間のベクトル（点）データを平面で分割するスキームである。

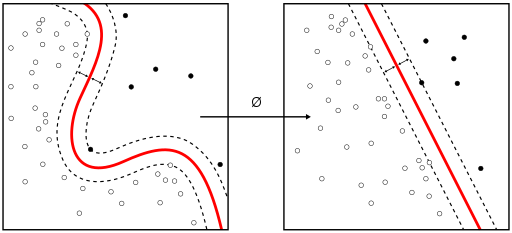
上の右図のように、境界が平面であればそのままでよいが、左のように境界が曲がっている可能性がある場合は、平面になるように変換する必要がある。その関数を$\boldsymbol{\phi}$と書く。左の図が$\boldsymbol{x}$の空間で、右が$\boldsymbol{\phi}$の空間であると考えれば良い。

そうすると、次のような線形識別問題なる。

(図は、https://qiita.com/pesuchin/items/c55f40b69aa1aec2bd19 より引用)

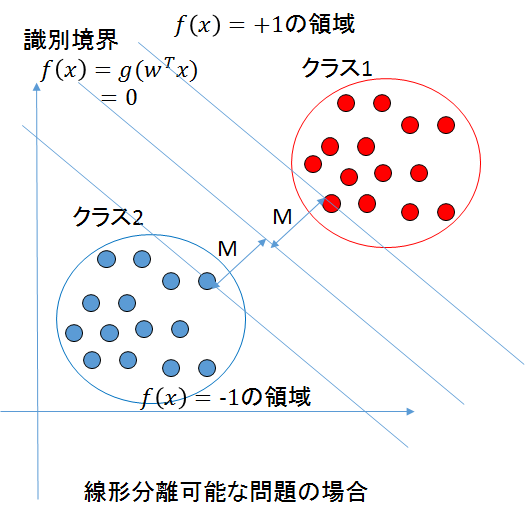
別のページにプログラムを付属して解説するが、sciki-learnのsvm計算の具体例を以下に載せる。

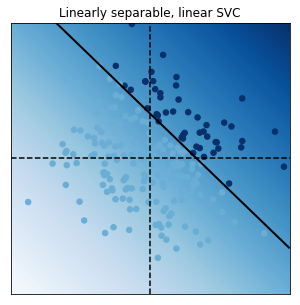
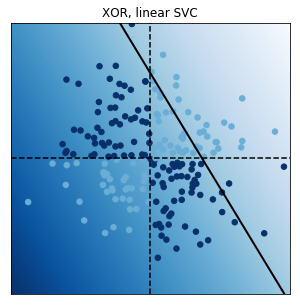
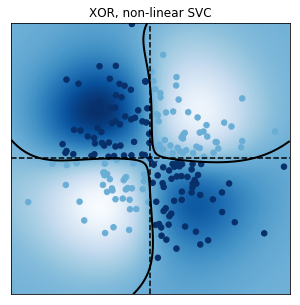
非線形な変換を施した説明変数$\boldsymbol{\phi}$に対して目標変数が

$$ y(\boldsymbol{x}_i)=\sum_{k=1} w_k \phi_k (\boldsymbol{x}_i) +b $$

のように線形な関係で表されるとして、係数を$\{w_i\,|\, i=1,\cdots M\}$を学習により決める。(以下ではまとめてベクトル$\boldsymbol{w}$で表す。ここでの添字$i$はベクトルの$i$成分ではなく、データの番号を表すことに注意してほしい。）

このような$\{\phi_1(\boldsymbol{x}), \phi_2(\boldsymbol{x}),\cdots , \phi_M(\boldsymbol{x})\}$を「基底関数」という。以下、これを太字$\boldsymbol{\phi}$で表す。 説明変数$\{x_1, x_2,\cdots , x_M\}$の非線形関数$\boldsymbol{\phi}$を用いれば、うまく平面の境界が得られると想定している。

分類問題なので、$f(\boldsymbol{x})$の値によって$\pm 1$をとる変数$t_i$を目標変数となるように変換しておく(正規化)：

• $t_i=1$のとき$\boldsymbol{w}^T\boldsymbol{\phi}_i +b \ge 1$
• $t_i=-1$のとき$\boldsymbol{w}^T\boldsymbol{\phi}_i +b \le 1$

まとめると、すべてのデータについて

$$ t_i(\boldsymbol{w}^T\boldsymbol{\phi}_i +b) \ge 1 \tag{1} $$

が成り立てば分類が成功だと判断できる。このとき等号が成り立つ場所が境界線で、それに近い一定の幅（マージン）上にあるデータをサポートベクトルと呼ぶ。 (境界から離れているので計算の対象としなくてよい。）

係数$\boldsymbol{w}$を過学習にならなく、かつ最適な値になるように決める。具体的には 式(1)の制約のもとで

$$ L_p(\boldsymbol{w}) = \frac{1}{2}\boldsymbol{w}^T\boldsymbol{w} $$

が最小となる$\boldsymbol{w}$を求める。(マージンが最大になる。)

ラグランジュ未定定数法を用いると、未定定数を${\alpha_1,\cdots, \alpha_M}$として

$$ \tilde{L_p}(\boldsymbol{w}) = \frac{1}{2}\boldsymbol{w}^T \boldsymbol{w} -\sum_{i=1}^{N}\alpha_i \{t_i(\boldsymbol{w}^T\boldsymbol{\phi}_i +b) -1\} \tag{2} $$

の条件なし極値問題を解くことになる。

$\boldsymbol{w}$の微係数がゼロという条件は

$$ \boldsymbol{w} - \sum_{i=1}^{N} \alpha_i t_i \boldsymbol{\phi}_i = 0 \tag{3} $$

bでの微分がゼロという条件は

$$ \sum_{i=1}^{N}\alpha_i t_i = 0 \tag{4} $$

となる。（他の条件の詳細は省く。）これにより、はじめにほしかった係数$\boldsymbol{w}$がきまる。ただし、このとき$\boldsymbol{\alpha}$がパラメータとして入っている。

(2)式を(3)に代入して、整理すると目的関数は$\boldsymbol{\alpha}$を変数として

$$ L_d (\boldsymbol{\alpha})= \sum_{i=1}^{N} \alpha_i + \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j t_i t_j k(\boldsymbol{\phi}_i, \boldsymbol{\phi}_j),\qquad k(\boldsymbol{\phi}_i, \boldsymbol{\phi}_j) = \boldsymbol{\phi}_i^T\boldsymbol{\phi}_j $$

と表される。これを最小にする$\boldsymbol{\alpha}$を求める問題に置き換わったのである。

この$k(\boldsymbol{\phi}_i, \boldsymbol{\phi}_j)$をカーネルと呼ぶ。（カーネルはSVMに限らずもっと広く機械学習の手法で登場する。ただし定義は同じである。）

$\boldsymbol{\phi}_i$は、もともとの説明変数$\boldsymbol{x_i}$の非線形変換$\boldsymbol{\phi}_i = \boldsymbol{\phi}(\boldsymbol{x_i})$であったとことに注意しよう。カーネルは２つの$\boldsymbol{\phi}$の積になっているが、そのことを忘れ（遡らず）、$i$, $j$の添字をもつベクトルからなる行列とみて、この極値問題を考えることにする。（かってに$k(\boldsymbol{\phi}_i, \boldsymbol{\phi}_j)$を選んだときにも、それに対応する非線形変換関数が存在することは証明されているらしい。)

そこで、もとの変数$\boldsymbol{x}$を用いて$k(\boldsymbol{x},\boldsymbol{x'})$のように書くことができる。(もちろん単純な積ではない。カーネルは２つの特徴ベクトルの関数であるというだけである。）

$$ L_d (\boldsymbol{\alpha})= \sum_{i=1}^{N} \alpha_i + \frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j t_i t_j k(\boldsymbol{x}_i, \boldsymbol{x}_j) $$

カーネル関数は、原理的に導けるものではなく、良いものを選べばよいという立場で考えていく。（このような行き方はカーネルトリックと呼ばれる。）

多くの場合、２つのベクトルの距離$||\boldsymbol{x}- \boldsymbol{x'}||$の関数を選ぶのが妥当とされている。距離の関数なのでradial basis kernel(RBF)と呼ばれる。また、近い点ほど関係が深いとして関数としてはガウシアンがよく用いられる。

$$ k(\boldsymbol{x},\boldsymbol{x'}) = \exp ( -\gamma ||\boldsymbol{x}- \boldsymbol{x'}||^2) $$

これがガウシアンカーネルである。カーネルとして、べき関数やロジスティック関数が用いらることもあるようだ。

重要な点は、必要な非線形変換$\boldsymbol{\phi}(\boldsymbol{x})$を指定しなくてもカーネルを適当に定めて、境界線を引けるということである。

新しいデータ点$f(\boldsymbol{x})$を分類するには、カーネルと学習によって得られた係数を用いて $$ y(\boldsymbol{x}) = \sum_{n=1}^N a_n t_n k(\boldsymbol{x}, \boldsymbol{x_n}) + b $$ のように表される。改めて、最初に仮定した非線形変換(基底の変更) $\boldsymbol{\phi}(\boldsymbol{x})$ がどのようなものかが表に現れなくなっていることに注意しよう。結果はうまく分類できたが最初の非線形変換$\boldsymbol{\phi}(\boldsymbol{x})$は意味がなくなった、原理的には存在するが、それを明示的に求める手法はない（必要ないから求めない）といっても良いと思う。

境界付近でデータが入り組んでいる場合：スラック変数の導入

多くの場合は、境界を明確に線引きできず、データは入り組んでいる。逆の領域に入り込んだ変数の対してスラック変数 $\xi_n$ を付与することにより、スラック変数の全体和が小さくなるような変分問題を考える。 $$ C\sum_{n=1}^N \xi_n + \frac{1}{2}||\boldsymbol{w}|| $$ 両者の重み付けパラメータ$C$は、問題に応じて外から与える必要がある。

scikit-learnを用いたプログラム例（授業では演習として取り上げる）

http://8tops.yamanashi.ac.jp/~toyoki/lectures/simulationsMethods/svc_in_scikit-learn.html