scilab関係

マニュアル、解説など

• scilab 5.3.0のマニュアル
• http://scilabinfo.wordpress.com/ 各種情報へのポータルとして有用（充実している。）
• scilab入門（日本語版pdf） 市販のテキストよりこれの方がよいかもしれない。（１００ページ以上ある。）

Tips

関数を定義したファイルの読み込み

• scilabのプログラムは、拡張子.sceをつけたファイルとする。実行するプログラムのファイルではなく、関数定義だけを保存するファイルは.sciという拡張子をつける。
• scilabを立ち上げて,「開く」からsciファイルを開く。
• エディタに読み込まれるので,その画面で、実行すれば,コンソールにて、sciファイルで定義された関数を使うことができる。（次節の例を参照）

組み合わせ(combination)

組み合わせ n!/(k!(n-k)!) の計算は、matlabではnchoosek(n,k)だが（高橋くんの発見）、scilabにはない。 scilabには備わっていないので、次のように独自に関数を作る必要がある。¹ （もちろん、下の例にあるコメント行はなくてもよい。必要なのは6行だけ。）

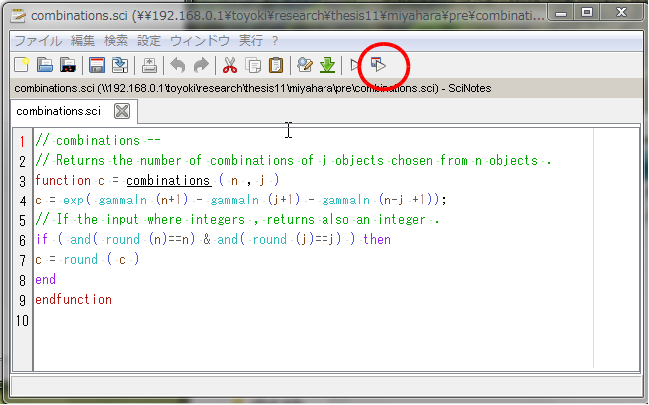
// combinations --
// Returns the number of combinations of j objects chosen from n objects .
function c = combinations ( n , j )
c = exp( gammaln (n+1) - gammaln (j+1) - gammaln (n-j +1));
// If the input where integers , returns also an integer .
if ( and( round (n)==n) & and( round (j)==j) ) then
c = round ( c )
end
endfunction

上記をcombinations.sciというファイルにセーブしておき、scilabで読み込むと（もちろん、scilabのeditツールを利用して書いてもよい。）次のようなscilabのeditツールに読み込まれる。これを丸印あるいは、「実行」メニューにより実行するとscilabのコンソールに読み込まれ実行される。

それが終わればコンソールにて関数combinations(10,5)のように実行できる。

微分方程式

miyahara.html参照

脚注

1. 関数combinationsの中で使われているgammalnは対数ガンマ関数と呼ばれるものである。ガンマ関数は簡単に言えば、階乗の実数への拡張である。つまり(2.3!)というようなものをΓ(3.3)と表す.これは積分で定義することができる。詳細は、http://www.scilab.org/support/documentation/tutorialsにある "Introduction to discrete probabilities with Scilab"を参照。 なぜ、階乗やコンビネーションを計算するのにΓ関数を使うのかは、このチュートリアルにもかかれているが、考えてみてほしい。20!/(5!15!)のようなものを単純にコンピュータで計算するのは精度、メモリー上、困難があるのである。