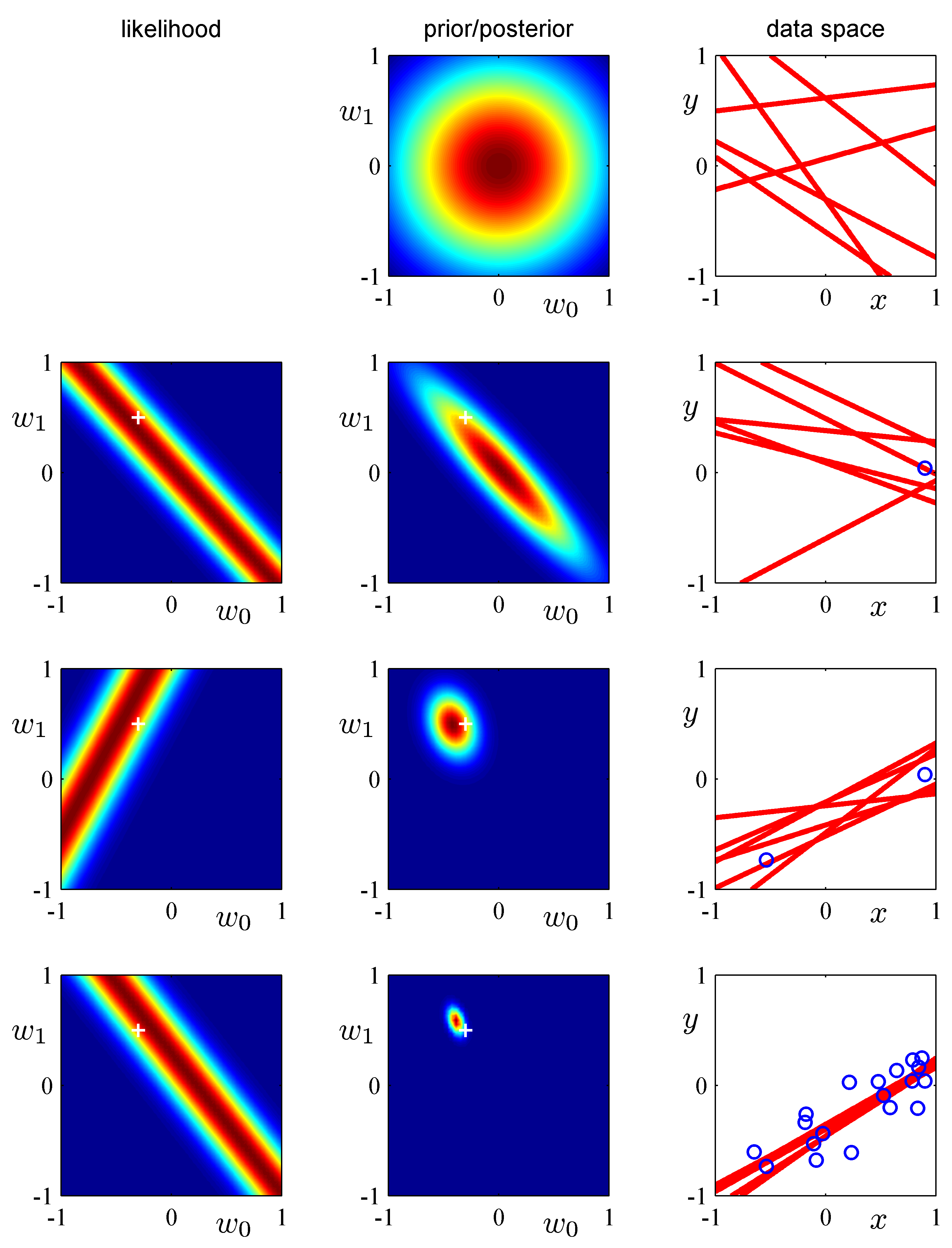
(注) 図中の"+"記号は、真の値(観測者は知らない)を表す。
The more a machine learning, the smarter it becomes.
機械学習は基本的にベイズ理論をベースにしている。一方、ベイズではない(それ以前の)方法は「古典的確率(classical probability)」あるいは「頻度主義的(frequentist)」な確率解釈と呼ぶ。
Wikipedia: https://ja.wikipedia.org/wiki/%E3%83%99%E3%82%A4%E3%82%BA%E7%B5%B1%E8%A8%88%E5%AD%A6
下に示すような、条件付確率の概念を統計予測に適用する手法をベイズ統計予測と呼んで、素朴な頻度主義統計の考え方とは異なると解説してある記述が多いが、これがなかなかわかりにくい。前回のページと重複するが、改めて、そこを解説したい。
以下の記述は主に、「パターン認識と機械学習」(C.M. ビショップ、丸善, 原著 "Pattern Recognition and Machine Learning")にもとづく(以下、PRMLと略す)。原著の最新情報は https://research.microsoft.com/~cmbishop/PRML/ より得られる。図表がここから得られる。以下ではそれを利用している。
PRMLの日本語版のページは、http://ibisforest.org/index.php?PRML
確率の基本ルール:
Sum rule $$ p(X) = \sum_{Y} p(X,Y) $$
Product rule $$ p(X,Y) = p(Y|X) p (X) $$
$p(Y|X)$は、ある事象(データ)Xが与えられたもとでのYが起こる条件付確率である。
$p(X,Y)=p(Y,X)$であるから、$ p(Y|X) p(X) = p(X|Y)p(Y)$。これを変形すると
$$ p(Y|X) = \frac{p(X|Y)p(Y)}{p(X)} $$と書ける。これをベイズの定理という。 あるデータ$X$が得られる前の$Y$の確率$p(Y)$を事前確率、$X$が得られたもとでの$Y$の確率$p(Y|X)$を事後確率と呼ぶ。
これが基本であるといっても、なんでそれがありがたいの?ということになるだろう。これが機械学習にどう具体化されるのかを以下に述べる。
ちなみに、当たり前のような上記の分母は、Yが取りうるすべての値について確率の和をとったら1になるようにするために書いておく。 $$ \sum_Y p(Y|X) = \frac{1}{p(X)}\sum_Y p(X|Y)p(Y) = 1 \quad {つまり}\quad p(X) = \sum_Y p(X|Y)p(Y) $$
この式は、学習した確率分布をもとに「予測」を行うのに用いられる。
テストデータを用いて関数近似を行う問題、つまり、観測データから関数近似の係数を予測する問題では、$X$は観測データ$\mathcal{D}$、$Y$はフィッティング関数の係数${\bf w}$に対応させて
$$ p({\bf w}| \mathcal{D}) = \frac{p(\mathcal{D}|{\bf w})p({\bf w})}{p(\mathcal{D})} \tag{*} $$のような意味合いになる。分母は単なる係数なので、実質的に
$$ p({\bf w}| \mathcal{D}) \propto p(\mathcal{D}|{\bf w})p({\bf w}) $$を用いる。 また、(*)を${\bf w}$で積分すると、確率が1に規格化されているとして、 $$ p(\mathcal{D}) = \int p(\mathcal{D}|{\bf w})p({\bf w}) d{\bf w} $$ となる。これはある観測データが得られる確率を、${\bf w}$の確率に、その${\bf w}$のもとで事象$\mathcal{D}$が得られる確率をかけて積分することにより得るというのが以下のベイズ予測プロセスである。
この式に基づいてデータから係数${\bf w}$の確率分布が得る作業を行う。なお、右辺の$p(\mathcal{D}|{\bf w})$は尤度(likelihood) と呼ばれる。 補足説明
訓練データとして、説明変数${\bf x}=\{x_1, x_2, \dots, x_N\}$に対する目的変数の値${\bf t}=\{t_1,t_2, \cdots, t_n\}$が与えられたとき、テストデータの値$x$に対する目的変数の値$t$を推定することを行いたい。目的変数は複数でもよいのだが以下では簡単に1つとして$t$で表す。
$x$とtの関係としてはたとえばべき関数を想定すると $$ t = y(x, {\bf w}) = w_0 + w_1 x + w_2 x^2 + \cdots + w_M x^M = \sum_{j=0}^{M} w_j x^j $$ のようにかける。係数をベクトル${\bf w}^T = (w_0, w_1, \cdots, w_M)$、各べきを${\bf \phi}^T = (1, x, x^2, \cdots, x^M)$のようにあらわすと、$t={\bf w}^T{\bf \phi}(x)$のよう書くことができる。以後このような表記をする。
(注) 最小2乗法による${\bf w}$の決定は、ここでいう「古典的確率解釈」に対応する。
ベイズ統計の肝は、
あたらしいデータ$x$に対して、目的変数の値が$t$になる確率は $$ p(t|x, {\bf x},t) = \int p(t|x, {\bf w}) p ({\bf w}| {\bf x}, t) d{\bf w} \tag{1} $$ で与えられる。
データが追加されるごとに、ベイズの条件付確率の式に従って、$p ({\bf w}| {\bf x}, t)$を更新する。
そのことを、PRMLの第3章「線形回帰モデル」にある図を使ってベイズ統計を線形回帰に適用する事例を説明する。
まずは、線形回帰(上記の、べき関数において、$M=1$の場合)について考える。
下の例は、サンプルデータとして、 $y=ax + b$, $a=0.5$, $b=-0.3$の周りに標準偏差$0.2$でランダムに発生させる。
線形回帰式
$$ y(x,{\bf w}) = w_0 + w_1 x $$として、データを与えるごとに、係数${\bf w} = (w_0, w_1)^T$の確率分布がどのように変化していくかを図示したものである。
最初は何もわからないので、初期の事前分布は$w_0=w_1=0$を中心とするガウス分布としておく。(下の図の1段目の真ん中の図) 測されたとする。その時の尤度($(w_0, w_1)$に対してある$(x,y)$が生ずる可能性)は2段目左のようになる。与えられたデータが$(x_1,y_1)=(0.9, -0.1)$だとすると、それを生じさせる$(w_0,w_1)$は、$0.9w_1 + w_0 =-0.1$、つまり$w_1 = -(1/0.9) w_0 + 1/9$のような直線の周りのガウス分布となる。それを描いたのが2段目左の図である。(ここがわかりにくいかもしれない。$(w_0, w_1)$の値が条件で、その条件のもとで、データ$(0.9, -0.1)$が得られる確率を$(w_0, w_1)$の面に描いているのである。)
このときの事後確率は、事前確率(上の2列目)と尤度(左図)の掛け算で与えられ、2列目の図のようになる。右図は、その事後確率に基づいていくつかの直線を発生させたものである。
2つ目のデータが3段目の右図の〇のように得られたとき、その尤度は3段目左図のようになり、その前の確率に尤度をかけて事後確率を得る。
これを繰り返すと事後確率は$(0.5,-0.3)$を中心とする狭いガウス分布に収斂していく。

(注) 図中の"+"記号は、真の値(観測者は知らない)を表す。
ここで理解してほしいのは、データを与えるごとに、仮定した関数(ここでは線形関数)の係数$(w_0, w_1)$の値の範囲がどんど狭められていくということである。
これが、これを「学習」ととらえてもよいだろう。
前項ではもっとも簡単な線形関数へのフィッティングを例にベイズ統計の図的理解を述べた。
その拡張としてフィッティング関数の一般化を図る。
前回には、多項式関数へのフィッティングを扱った。すなわち、 $$ y(x, {\bf w}) = w_0 + w_1 x + w_2 x^2 + \cdots + w_M x^M = \sum_{j=0}^{M} w_j x^j $$ のように選び、$M+1$個の係数の最適値を選んだ。
一般には、べき関数でなくてもよく、何らかの関数の組 $\{\phi_i (x)\}$ ($i=1,\cdots, M$)を選び、その線形結合で説明変数と目的変数の関係を書き表す。説明変数は1個ではないので、$x$はベクトルになる。その際には関数$\phi$もベクトルになるので、まとめて太字の${\bf \phi}$で表す。 $$ y(x)= \sum_{i=0}^{M-1}w_i\phi_i(x) = \boldsymbol{w}^T\boldsymbol{\phi}(x) \tag{2} $$
このような関数の組を「基底関数」と呼ぶ。
多項式の場合は、$\phi_n (x) = x^n$以外に、そのほかによく用いられるものとして、ガウス関数 $\phi_n(x) = \exp [-(x - \mu_i)^2/2s^2]$や、シグモイド関数がある。
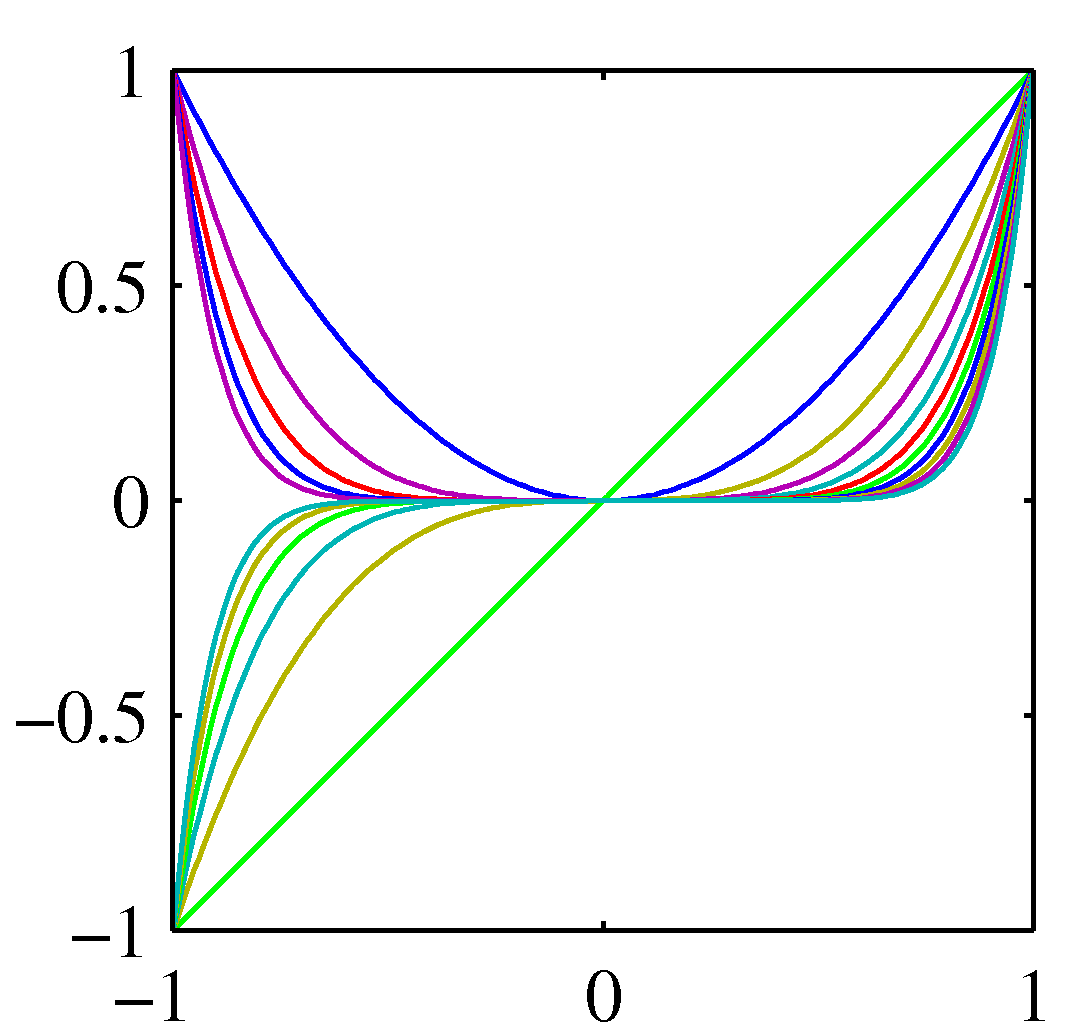 ガウシアン
ガウシアン
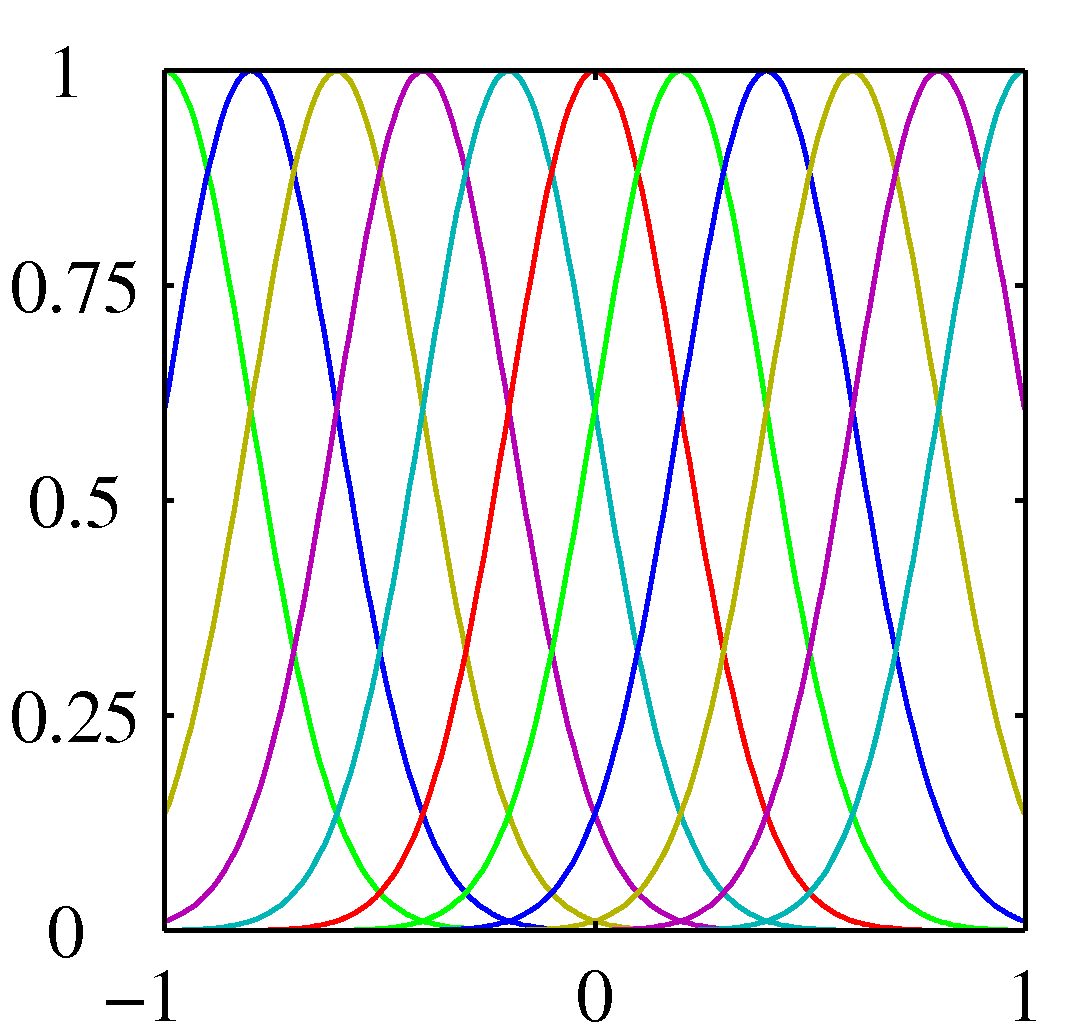 シグモイド
シグモイド
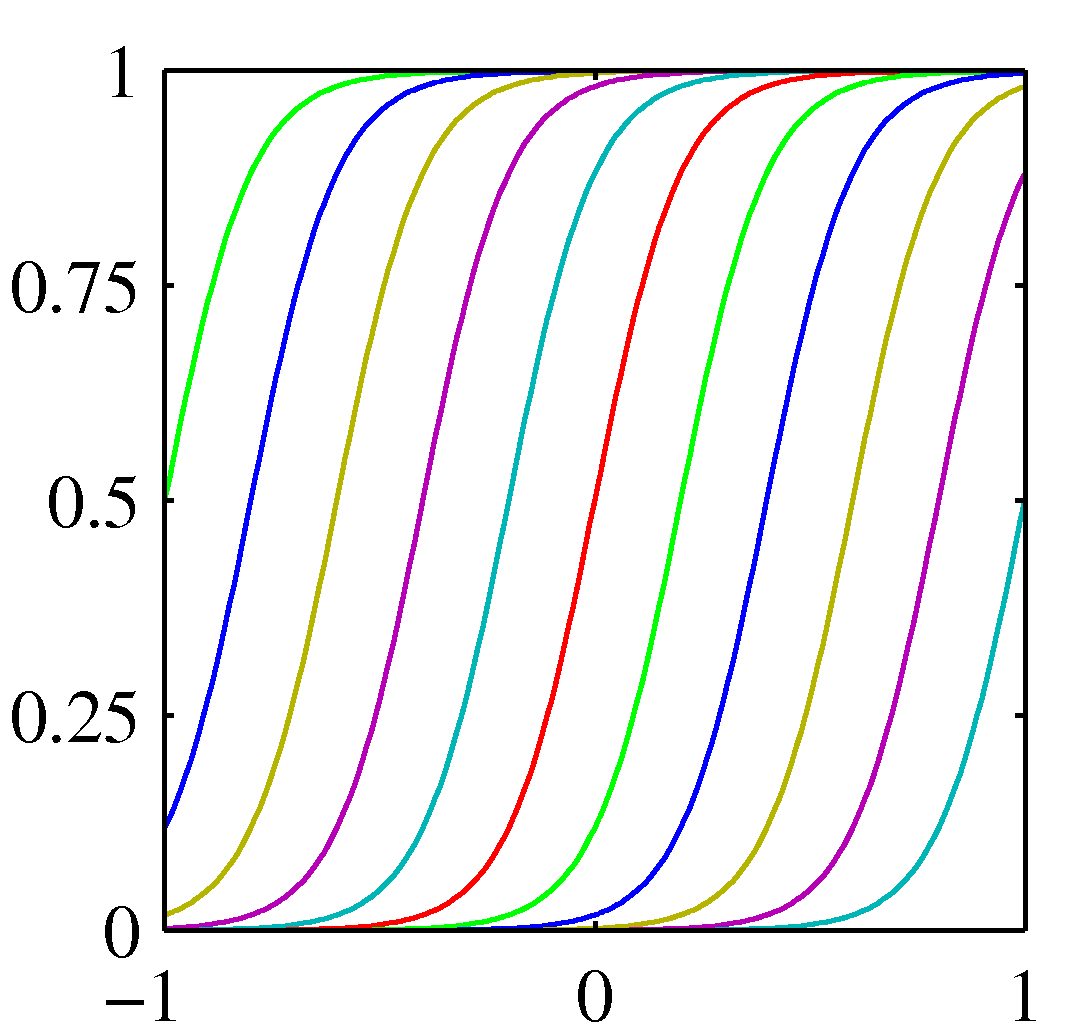
(一応、説明はするがコンピュータ関係のコース以外はとばしてもよい。)
ベイズ統計推定は、目的変数の分布が、事前確率分布とデータから得られる尤度関数の積によって与えられる。
両方ともガウス分布で与えられると仮定して、データにより目的変数の推定値分布がどのように限定されていくかの説明が PRML第3章でに述べられている。
事前分布をガウシアン(平均値$0$, 分散を$\alpha$)選ぶと、${\bf w}$の事後分布もガウシアンになる(ノイズを分散$\beta$のガウス型として)。
ベイズ予測は、(1)式と同様だが $$ p(t|{\bf x},{\bf t},\alpha, \beta) = \int p(t|{\bf w},\beta) p ({\bf w}|{\bf x}, {\bf t}, \alpha, \beta) d{\bf w} \tag{3} $$ 言葉で表すと $$ ({\rm prob.\ of\ target\ } t {\rm \ for\ a\ given\ training \ data\ set\ } \{{\bf x}, {\bf t}\}) = \int_{\bf w} ({\rm prob.\ of\ } t {\rm \ for\ }{\bf x}{\rm \ under\ } {\bf w}) \times ({\rm prob.\ of\ }{\bf w}{\rm \ calculated\ from\ a\ training\ data\ set\ } \{{\bf x}, {\bf t}\}) $$
被積分関数である、$t$の条件付分布(${\bf w}$を用いて(2)式より計算される値からのずれの分布)と${\bf w}$の事後分布の両方はともにガウシアンであるので、積分の計算ができる。
訓練データを用いて計算する${\bf w}$の事後分布は $p ({\bf w}| {\bf t}, \alpha, \beta)$はガウシアンになると仮定する。事前分布の平均値はゼロ、分散は$\alpha$、母集団での目的変数の分散を$\beta$とすると、平均と分散は $$ {\bf m}_N = \beta {\bf S}_N {\bf \Phi}^T {\bf t},\quad {\bf S}_N = (\alpha {\bf I} + \beta {\bf \Phi}^T {\bf \Phi})^{-1} \tag{4} $$ で与えられる。
また、${\bf w}$が与えられたときの、$t$の確率分布は $$ p(t|{\bf w},\beta) = \mathcal{N} (t| y({\bf x}, {\bf w}, \beta^{-1})) $$ とする。
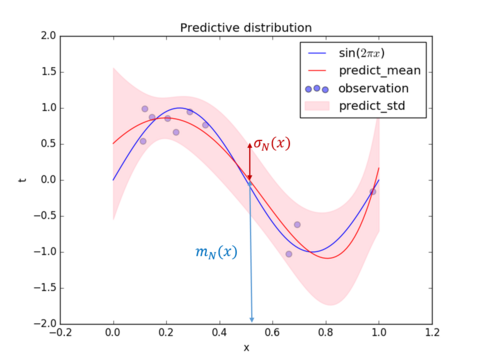
以上を用いて、(3)の積分を実行すると 目的変数$t$の分布は次のようなガウシアンになる。ガウシアンを$\mathcal{N}$で表す。ガウシアンは、平均値と分散だけによって特徴づけられることに注意しよう。これは、[以前の図](https://toyoki-lab.ee.yamanashi.ac.jp/~toyoki/lectures/PracDataSci/images/prmlfigs-png/Figure1.16.png)の縦棒に書かれた分布$p(t|x_0, {\bf w}, \beta)$に相当するものである。 $$ p(t|x, {\bf x},{\bf t}) = \mathcal{N}(t| m_N, s_N^2(x)) \tag{5} $$ 目的変数$t$の予測分布の平均は $$ m_N = {\bf m}_N^T \phi (x) = \beta \phi (x)^T {\bf S}_N \sum_{n=1}^N \phi (x_n) t_n \tag{6} $$ 分散は $$ \sigma_N^2 = \beta^{-1} + \phi (x)^T {\bf S}_N \phi (x) \tag{7} $$ で与えられる。(平均値$m_N$が上の図の赤線、標準偏差$\sigma_N$はピンク帯の片方の幅に相当)
説明変数$x$の値を使ってに、目的変数$t$の分布が平均値$m$、標準偏差$\sigma$で与えたことになる。 $\sum_n$の部分が$N$個のデータから計算される。
サンプルデータをつくって、この式に基づいた推定を行ってみると、前節のような図が得られる。
(注) (4)のようなガウシアンの対数をとると、 $$ \ln p({\rm w}|{\rm t}) = -\frac{\beta}{2}\sum_{n=1}^N \{t_n - {\bf w}^T\boldsymbol{\phi}({\bf x}_n)\}^2 -\frac{\alpha}{2}{\bf w}^T{\bf w} + ({\rm const.}) $$ のように書くことができる。この対数尤度の極値(最も尤もらしい${\bf w}$)は、Ridge回帰により${\bf w}$を求めることと同等であることがわかる。
数値計算については後で述べるが、上の定義に沿って、与えられたデータ点から次のような平均と標準偏差を計算することができる。
前項に示した式を実際にプログラムした例が
https://qiita.com/ctgk/items/555802600638f41b40c5
にある。
繰り返しになるが、データが多い$x$の値のところでは偏差の幅が小さくなっており、値がないところは広がっていることに注意してほしい。
尤もらしい値(ベイズでは最尤解)は、この場合は、最小2乗法(リッジ回帰などを含む)の結果と一致する。
予測の中心(最も確率が高いところ)は各$x$での平均値$m(x)$で、幅(標準偏差)は$s(x)$で与えられる。上の図の青線の分布が、平均値$m(x)$、分散$s^2(x)$のガウス分布になっており、分散が場所$x$によって変化していることがわかる。
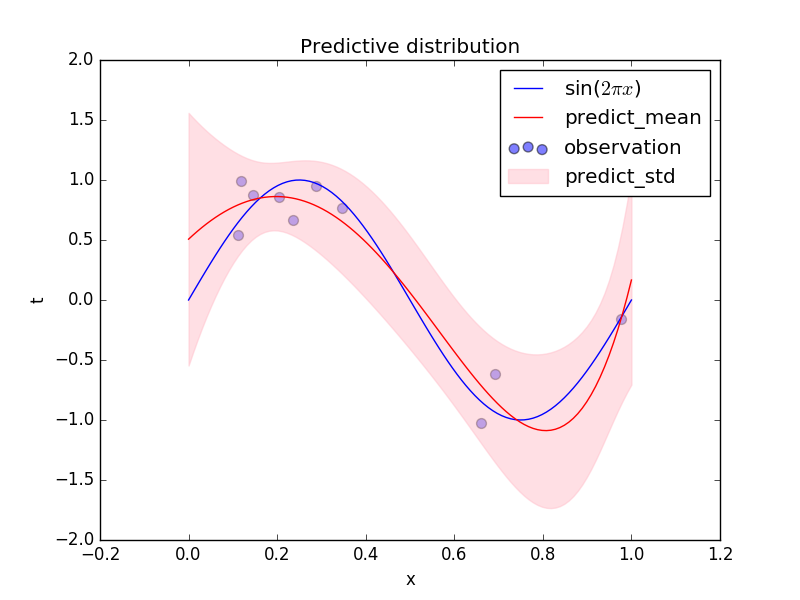
繰り返しになるが、データが得られるごとに推定(目的変数の確率分布)がどんどん変化していくことがベイズ推論(ベイズ統計)らしさである。
ここでは$M$次べき関数を用いて(これをモデルの選択という)フィッティングを行ったが、モデルの選択自体もデータから推定するいろいろな方法が開発されている。(図では$M=5$。)
さらに、いつも分布がガウス分布とは限らない。2項分布やポアソン分布と考えるべき対象もある。それも使う人の選択にゆだねられる。
基底関数を説明変数$x$の「べき」でなく、ガウス基底としたPRMLに載っている図の再現は、https://qiita.com/naoya_t/items/80ea108cebc694f5cd63 にある。
また、基底を特定することなく、確からしい曲線の範囲(上のピンクの帯)をデータから求める方法もある。その一つとしてカーネル法というのがあり、そのなかでも有力な方法がSVRである。(後述)
Web上に公開されているプログラム例:
この2つを参考に、両方の基底による推定を図示するプログラムを次のURLにおいてある。
https://toyoki-lab.ee.yamanashi.ac.jp/~toyoki/lectures/PracDataSci/prml3.3.html
このプログラムを実行して、データ数や基底の取り方によって予測がどのように変わるかを試してみよう。サンプルデータを作る関数やデータの個数を変えてみるとよい。
ここで扱った事後分布や誤差分布がガウシアンになる場合は、説明変数$x$に対する予測値は、事後分布の平均値(6)式のように $$ y(x, {\bf m}_N) = {\bf m}_N^T {\bf \phi} (x) = \sum_{n=1}^N \beta {\bf \phi}^T(x){\bf S}_N {\bf \phi}(x_n)t_n $$ で与えられる。
これを $$ y (x, {\bf m}_N) = \sum_{n=1}^{N} k(x, x_n) t_n, \qquad k(x,x') = \beta {\bf \phi}^T(x){\bf S}_N {\bf \phi}(x') $$ と書いたとき、$k(x,x')$を、平滑化行列(smoother matrix)あるいは等価カーネル(equivalent kernel)と呼ぶ。左辺は、訓練データの線形結合で表されていることに注目しよう。訓練データと「予測関数」の関係をこのように書くと、基底関数($\boldsymbol{\phi}(x)$)やその係数${\bf w}$は裏に隠れてしまっている。
より進んだサポートベクトル回帰(SVR)では、この等価カーネルが大きな役割を果たすことになる。SVRでは、$\phi (x)$を設定することなく、トレーニングにより、カーネル$k(x,x')$自体の関数形を設定し、パラメータをトレーニングにより決定することになる。
%%html
<link rel="stylesheet" type="text/css" href="custom.css">