ここでは、BishopのテキストPRMLに記載されている理論式(14.5節 Mixtures of liniear regression models)を直接プログラミングした事例を紹介する。PRMLの目次
混合モデルはわかりにくい用語で、英語名のとおり、複数の線形回帰モデルの混合と呼ぶ方が内容を反映している。あるデータを、複数の線形モデルが混ざり合っているものとして解釈するのが妥当な場合に適用する機械学習の方法である。
イメージをつかむためにPRMLの図を以下に掲げる。単純に線形回帰を行うと、
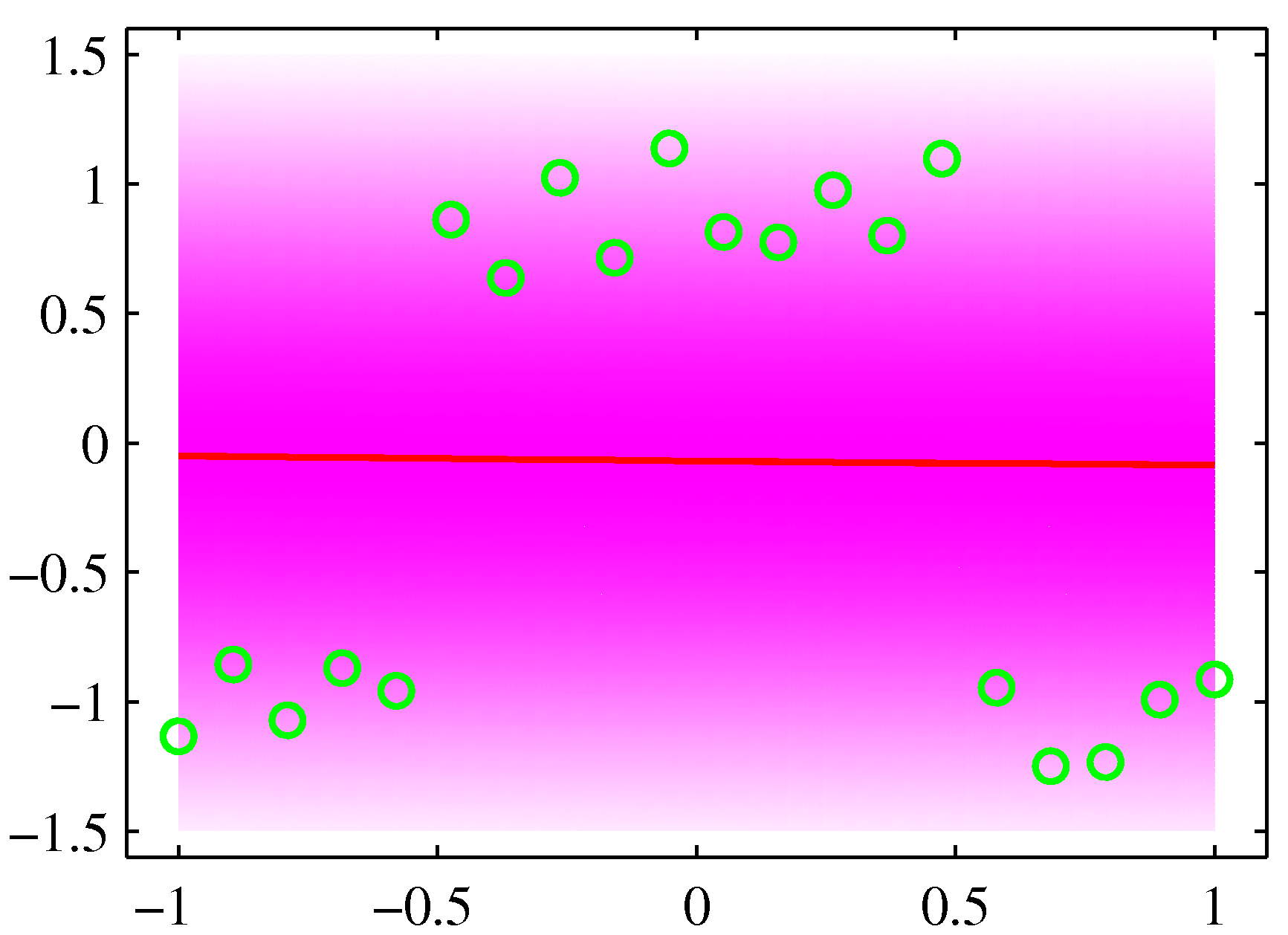
のようになるが、これは2つの線形関係をもつデータが混ざり合っていると解釈するのが妥当だろう。以下で述べる手法を用いると、
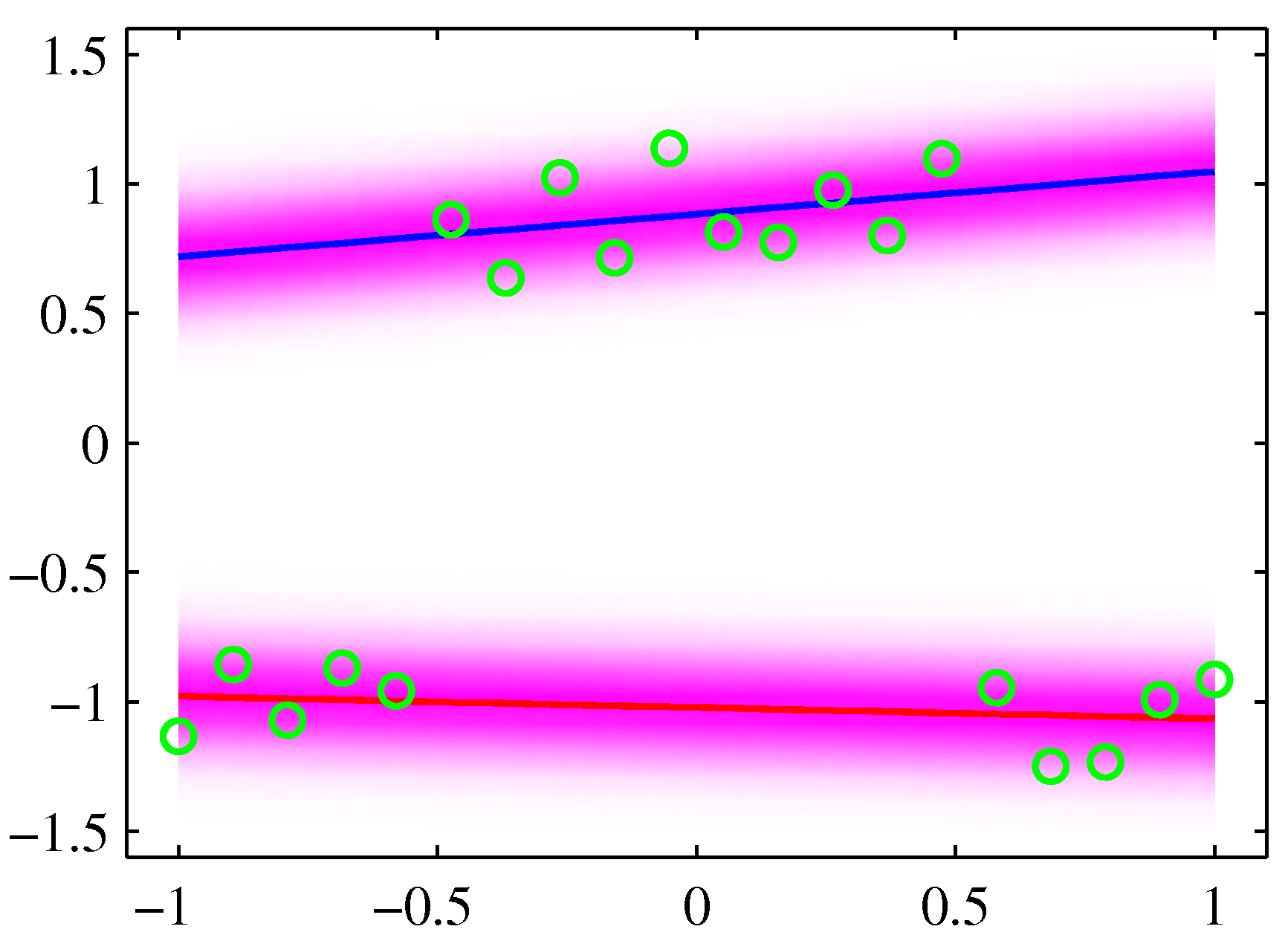
のように出力できる。
Scikit-learnにはGaussian Mixture Model
https://scikit-learn.org/stable/modules/mixture.html
として実装されているが、回帰問題への応用はなされていない。
回帰への適用については、GMRというライブラリが次のURL公開されているので、興味がある人は試してみてほしい。
