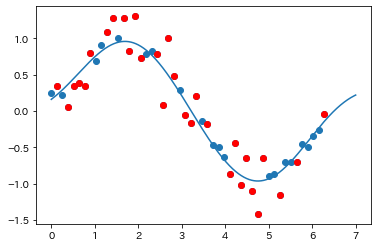
# scikit-learnの各種モデル
# {model, title(name), 説明変数, 目的変数, test(predict)用データ}の配列を用意する
models = {}
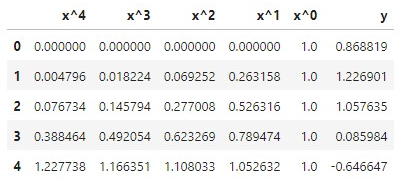
# 非線形回帰:多項式近似 (vander行列をデータとして入力 ⇒ 線形重回帰へ入力)
from sklearn import linear_model as lm
models['LM'] = {"model": lm.LinearRegression(),
"name": "Simple Polynomial Model " + str(deg) +"次",
"feature": poly_feature, "target": target, "test_data": test_poly}
# SVR
from sklearn import svm
models["SVR"] = {"model": svm.SVR(kernel='rbf'),
"name": "Support Vector Regression",
"feature": single_feature, "target": target, "test_data": test_single}
# RVR (pipでインストールする必要あり)
from sklearn_rvm import EMRVR
models["RVR"] = {"model": EMRVR(kernel='rbf', gamma="scale"),
"name": "Relevant Vector Regression",
"feature": single_feature, "target": target, "test_data": test_single}
# Neural Network
from sklearn.neural_network import MLPRegressor as MLPR
models["NN"] = {"model": MLPR((100,), activation="identity", solver="lbfgs",
max_iter=2000, tol=1e-8),
"name": "Neural Network",
"feature": scaled_poly_feature, "target": target, "test_data": scaled_test_poly}
# Random Forest
from sklearn.ensemble import RandomForestRegressor as RFR
models["RFR"] = {"model": RFR(max_depth=3, n_estimators=100), # 深さをいろいろ変えてみる
"name": "Random Forest Regression",
"feature": poly_feature, "target": target, "test_data": test_poly}
# Mixture model