ここでは,理解に役立つJavaScriptプログラムを掲載します.
自分で描いてみるには、pythonをおすすめします。
章,節,式の番号はテキスト(E.クライツィグ「フーリエ解析と偏微分方程式」)のものです.
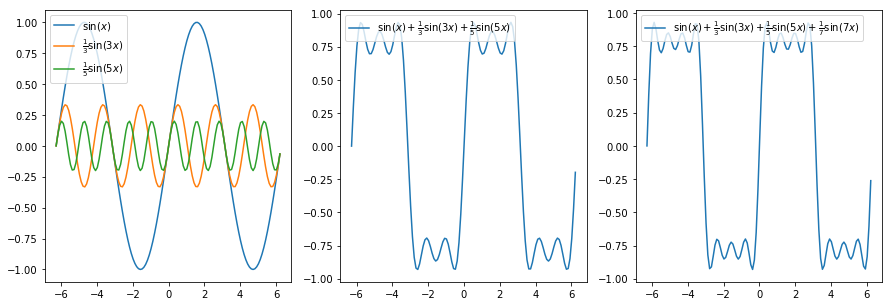
フーリエ級数の例として
\[
f(x) = \sin(x) + \frac{1}{3}\sin(3x) + \frac{1}{5}\sin(5x) + \cdots
\]
を描画してみます。

項をたくさん足し合わせることにより、方形波に似てきます。このような数列の和の項数を増やしていくとどのような関数にあるかを描くプログラムを用意しました。
方形波などのフーリエ級数を描画してみます.級数をn項までの近似関数を,nを増やしつつ描画してみると,次数が上がるに連れて目的の関数に近づくことが体感できます.
テキスト§2.2の例,問題に関連した級数を描画してみましょう.
上記リンクにあるプログラムはJavaScriptで作成されたものでありブラウザ内で実行してみることができますが、自分でプログラムを組んでみたいという人もいるでしょう。
いくつかの方法がありますが、python言語を利用してみることをおすすめします。
- pythonのプログラム・実行環境にはAnaconda3というパッケージをおすすめします(とくにWebブラウザで動くノートブック環境Jupyter)。インストールの仕方はWebページにたくさんあるので気に入ったものを参照してください。
- 数項の数例を描画するだけなら5行くらいで書けます。
外力が「三角波」の場合,振動子の固有振動数が「ほぼ」維持されることが,例1に示されています.微分方程式を数値計算し,その振る舞いを調べてみます.
斉次方程式の一般解にあたる減衰振動が消え,定常解(微分方程式の特殊解)が生き残る様子も観察してみましょう.
外力として三角関数を選ぶこともできるようにしてありますので,それとの比較も行なってみてください.
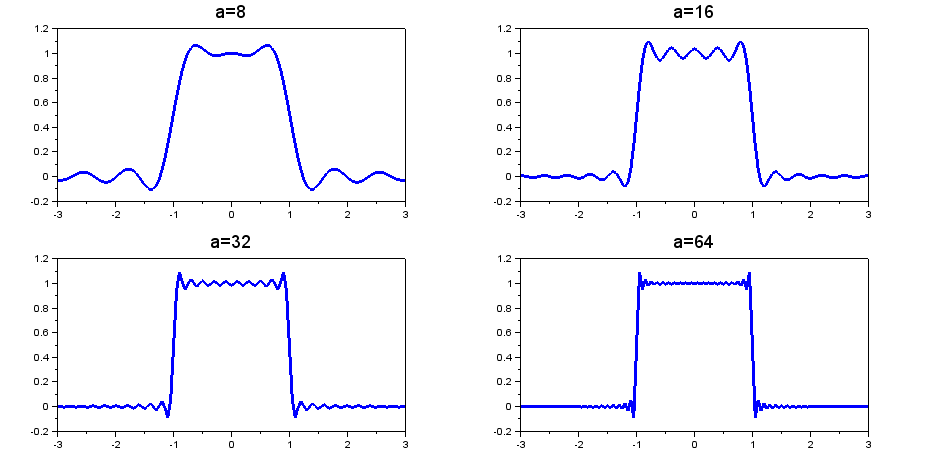
テキスト2.8節の例2「単一パルス」のフーリエ積分表示を有限区間の積分で止める近似 \( \displaystyle{\int_0^a \frac{\cos w x \sin w}{w} dw } \)
の図が、図2.22として載っている。
いくつかのaについて、数値積分してみる。
作成したscilabプログラムをここに掲載しておく。
様々な初期値での固定端波動方程式の数値計算
両端が吸収端である場合