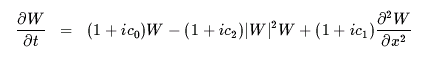
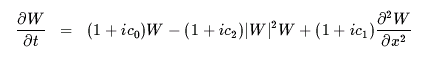
以下の図はpgplotを利用したCプログラムによるものです。(2001)
pythonスクリプトも作ってみました。(2018) (こちら)
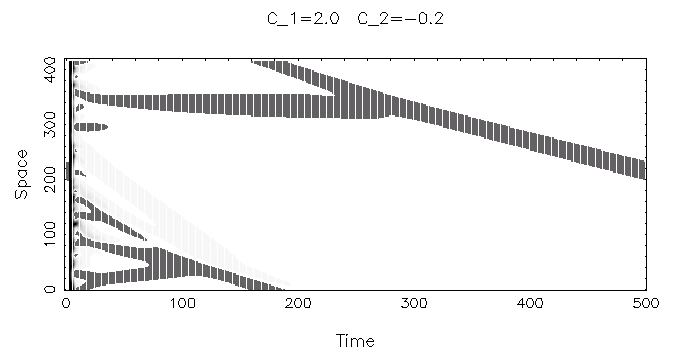
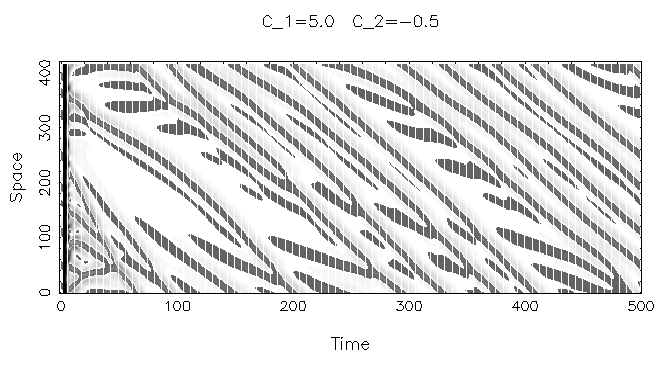
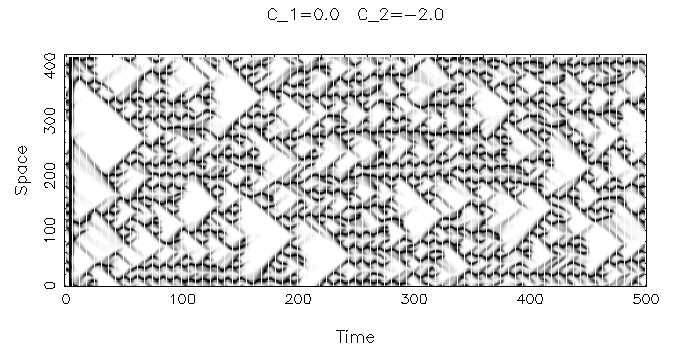
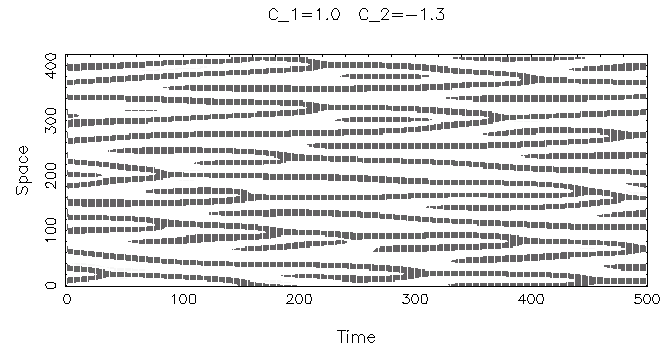
c1=0の場合について見てみましょう.この方程式は,励起の役割を 果たす1次の項と,散逸の役割を果たす3次があり,それに拡散項をつけたものです.係数の虚数部 (c0とc2)により開放系らしい振動が現れます.
1次元の320個の格子点のモデルで,右端を固定,左端はフリーという境
界条件,初期パターンは,W(0,0)=0.2, W(i,0)=0.0 (i≠0)として動かす
と,
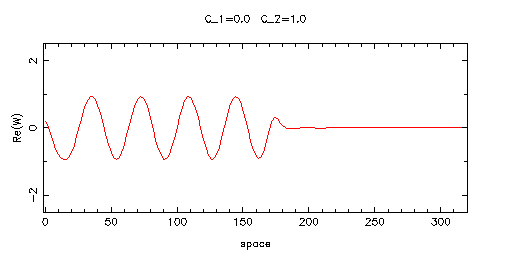
のように振動部分が左から拡大していきます.
プログラムを動かせない人のために,mpeg形式の動画をつくってみました. xanim等のmpegビューワがあれば見られます. (1次元ですから,計算しながら描画したほうが速いのですが...)
下の図のように,両側から波が発生していき
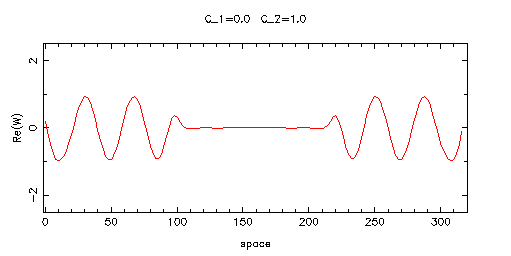
ぶつかったところで波は干渉し打ち消しあっているように見えます.
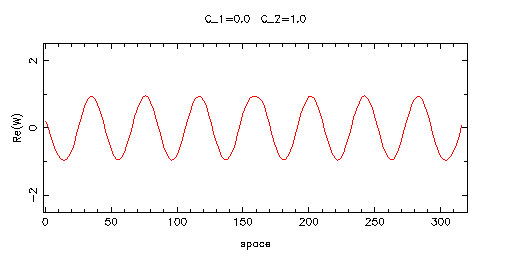
mpeg動画はこちらです.
説明は授業で行いますが,この方程式の一様振動解の安定性を調べると,
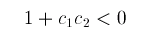
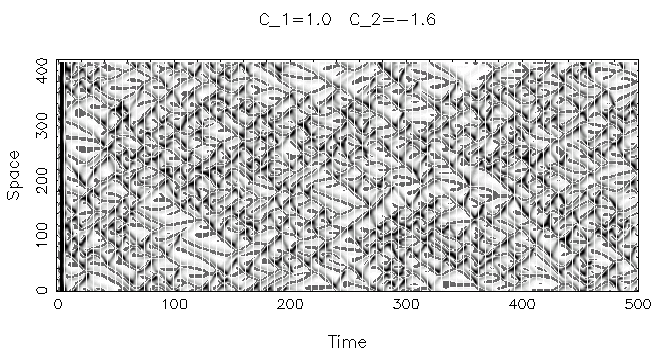
周期的境界条件にして,W<<0のランダムな微少揺ぎからから生ずる パターンを調べてみましょう.
パターンの特徴をとらえるために,ここでは振幅|W|の大きさを濃淡で表し, その時間変化を横軸に書いていってみます.