前処理¶
プログラムは、Webブラウザ内で動くものだけを使用しますが、ブラウザがInternet Exploreだとうまく動作しないことがあります。
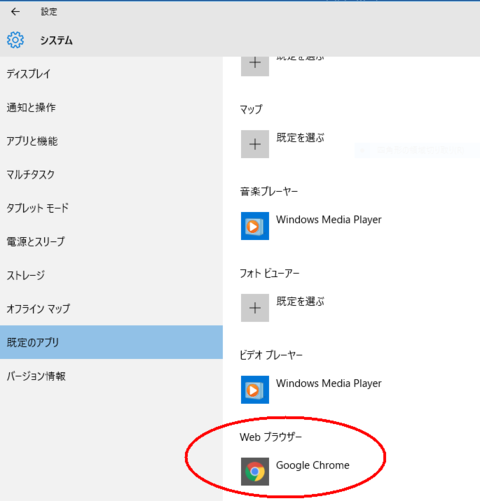
念のため、Windowsのメニュー「設定」から、下の図のように「設定>システム>既定のアプリ」でWebブラウザをGoogle Chromeにしてください。
1本の道路を多数の車が走る場合の数値シミュレーションを行います.直線的な高速道路のようなもっとも単純な道路においてさえ自然渋滞が発生しうることが理解できる数理モデルを数値計算(コンピュータシミュレーション)してみます。
まずは、下記URLの動画を見てください。
http://iopscience.iop.org/1367-2630/10/3/033001/media
最初に等間隔で走行している車列がちょっとしたきっかけで乱れたとき、元に回復せず部分的に混んだ状態(渋滞クラスタ)が生じてしまうことが見て取れます。高速道路での自然渋滞はこのような現象だと考えられています。
このような1本道の車の動きをあらわす数理モデルとして「最適速度モデル」(Optimal Velocity Model, OVモデル)というものがよく知られており、その派生モデルは現在でも研究されています。
この実習では、OVモデルを数値計算して動作を観察してみます。
最初にjupyterノートブック(以前はipython notebookと呼ばれた)の説明と操作練習を少し行い、そのあと最適速度モデルのシミュレーションを行い、レポートを作成します。
レポート作成は、Wordを用いることにしましょう。メモのために、早速、Wordを立ち上げておいてください。
プログラムは、Webブラウザ内で動くものだけを使用しますが、ブラウザがInternet Exploreだとうまく動作しないことがあります。
念のため、Windowsのメニュー「設定」から、下の図のように「設定>システム>既定のアプリ」でWebブラウザをGoogle Chromeにしてください。

プログラム言語pythonは、最近、データ解析や機械学習などに用いられることが多い人気言語で、さまざまな周辺ツールやライブラリがどんどん作られつつあります。ここでは、プログラムと様々な説明(通常の文章)を混在させることができるjupyter noteboookを利用します。
pythonはC等と異なり、インタプリタ型の言語です。スクリプト言語と呼ばれることもあります。Cのように、機械語に翻訳(コンパイル)してから実行するのではなく、実行段階で一行一行プログラムを読み取って実行していきますから速度は遅いですが、プログラムが簡単です。
プログラム上の大きな違いは、変数宣言をせずにいきなり使うことができる点です。変数の型もその場に応じて解釈されます(その解釈も時間がかる要因です)。
jupyter notebookはWindowsメニューから立ち上げます。ノートブックの編集、実行などの操作はWebブラウザ内で行われます。つまり、jupyterはpythonインタプリタの本体(バックエンド)とWebサーバ及び動的なページ(HTML5)を作成するシステムから成り立っています。
このページもjupyterを使って作成しました。
次のリンクは2つの実習用ノートブックファイルを圧縮したものです。クリックしてダウンロードし、ファイルを解凍して実習用フォルダの下に格納してください。
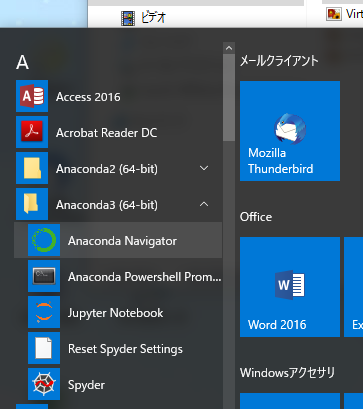
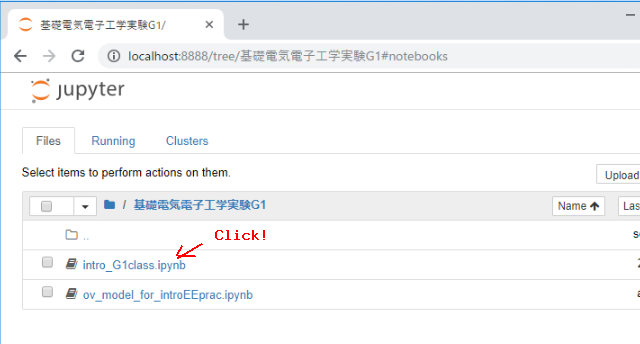
ここで、練習用ノートブックを使って、jupyterを操作する練習をします。(新規作成はしなくても構いません。)
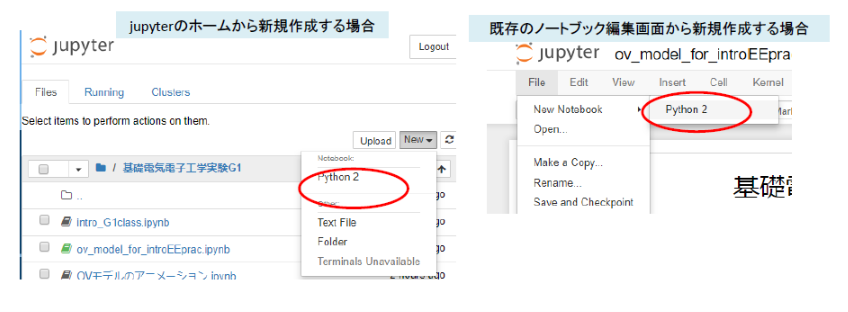
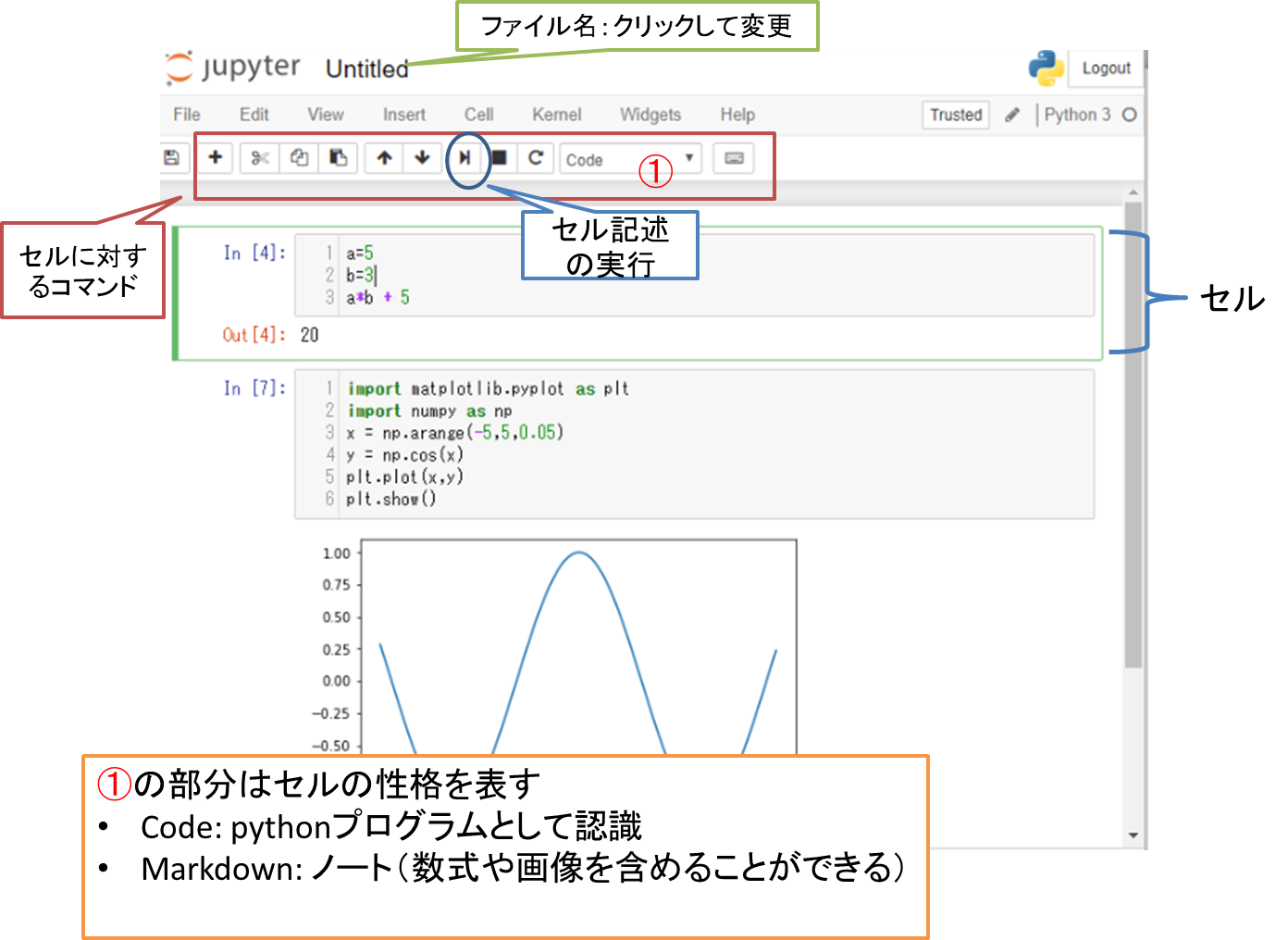
Web上にたくさんのチュートリアルがありますので、参考にしてください。
jupyterにはプルダウンメニュー以外にもたくさんの機能、機能に対するショートカットキーがあります。"Help"→"Keyboard Shortcuts"で一覧が表示されます。 日本語での紹介は、たとえば、http://qiita.com/masafumi_miya/items/6524dbd227705351a00c
jupyter notebookやpythonに関して試したこと、最適速度モデルのシミュレーションをやってみてわかったことを画像付きで報告してください。
作成は、Wordあるいはjupyter notebookで作成してください。Wordで作成した場合は、かならずpdf形式に変換して提出してください。ipynb形式の場合はそのままで結構です。(jupyterはpdf形式に変換する機能も備わっていますが、現在のところ日本語が入っているとうまく処理できません。工夫次第で可能になりますが、教室のパソコンでは無理です。)
提出は、レポートを電子メールに添付してtoyoki@yamanashi.ac.jp宛に送ってください。
以下に示す最適速度モデルのシミュレーションプログラムを実行し、「基本的なパラメータ」の値によって交通流がどのように変化するか(車の軌跡や空間パターンのスナップショット)を調べ、レポートを作成しなさい。
文書への画像の貼りこみは、Wordの場合は、「挿入」→「スクリーンショット」を用いるのが簡便です。
Markdownの記法はたとえば、http://qiita.com/tbpgr/items/989c6badefff69377da7 を参照してください。
実習時間が少ないので、詳細は理解できなくてもよいが、簡単に説明する。
実際の運転者の行動、車の動作は複雑ですが、もっとも本質的に重要なのは次のようなことだと考えられます。
加速・減速
車はN台あって、それぞれの速度と位置を$v_n(t)$, $x_n(t)$とし、番号$n$は進行方向に向かってつけることにし、微分方程式を書いてみましょう。まず、位置の変化は速度そのものですから、
$$ \frac{dx_n}{dt} = v_n $$
とあらわされます。速度の変化は加速度であり、上記の考えを
$$ \frac{dv_n}{dt} = a \left[ V(\Delta x_n) - v_n\right] $$
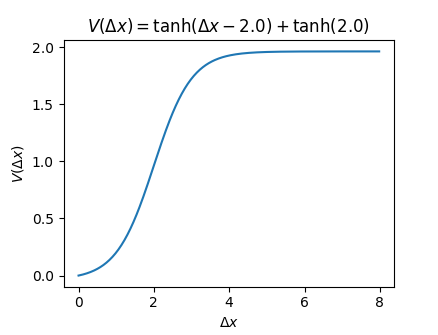
のように定義します(右辺は[力/質量]、この場合は人間の操作も含めた[車の駆動力/質量]を表します)。最適速度は$V(0)=0$であり、単調増加して一定値に近づく関数として
$$ V(\Delta x_n) = \tanh (\Delta x_n - c) + \tanh(c) $$
を採用します(上の図)。ただし、$\qquad n=0,1,2, .... ,N-1$であり、$n=N-1$の前は$n=1$、つまり周期的とします。
道路も実験のビデオと同様に周回道路とします。
"""
OVモデルの本体
"""
import numpy as np
from scipy.integrate import odeint
class ov_model:
def __init__(self, carNum, L, a, dt, initialize=True):
self.carNum = carNum
self.dt =dt
self.L = L
self.set_params(L,a)
if initialize:
self.initialize_x_v()
def set_params(self,L,a):
self.a = a
self.L = L
def initialize_x_v(self): # must call this after set_params
self.x = np.arange(0, self.L, self.L/self.carNum) # initial position
self.v = np.random.random(self.carNum) # initial velocity
self.x_v = np.concatenate((self.x,self.v))
self.x_v_trace = np.empty((self.carNum*2))
self.t_trace = np.zeros(1) # array of time for plot
self.present_time = 0.0
self.x_v_trace[:] = self.x_v # data for plot
def ov_eq(self, x_v, t, carNum, a, L):
'''
r.h.s of the ov equation
'''
x = x_v[:carNum]
v = x_v[carNum:]
x_fw = np.roll(x,-1)
delx = (x_fw- x + L) % L
return np.concatenate((v, a*(np.tanh(delx - 2.0) +np.tanh(2.0) -v)),axis=0)
def update_unit(self, n_steps, store_trace=False):
'''
solving the ov equation by "n_steps" iterations
'''
t = np.arange(0, n_steps*self.dt, self.dt)
new_x_v = odeint(self.ov_eq,self.x_v,t, args=(self.carNum,self.a,self.L))
self.x_v = new_x_v[-1] % self.L
self.present_time = self.present_time+self.dt*n_steps
if store_trace:
self.x_v_trace = np.vstack((self.x_v_trace, self.x_v))
self.t_trace = np.vstack((self.t_trace,np.array([self.present_time])))
def shift_x_v_t(self, n):
if n > self.t_trace.size:
n=-1
self.t_trace = self.t_trace[n:]
self.x_v_trace = self.x_v_trace[n:]
説明は後回しにして、次のセルをまずは実行してみる。
これは、横軸を時刻、縦軸を道路上の位置として車の軌跡を描くプログラムです。
主要なパラメータをGUI(Graphical User Interface)でセットできるようになっています。
次のことに注意して試してみてください。
%matplotlib nbagg
from ipywidgets import interact_manual, Checkbox, widgets
from IPython.display import clear_output, display, HTML
model = ov_model(50, 100, 1.5, 0.01, True)
def show_trace_ov(carNum, rho, a, initialize, max_t):
global model
unit_steps =10
dt=0.01
if initialize:
model = ov_model(carNum, carNum/rho, a, dt, initialize)
else:
model.shift_x_v_t(int(max_t/dt))
for i in range(int(max_t/dt/unit_steps)):
model.update_unit(unit_steps, True)
# plot the traces
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,5))
axes = fig.add_subplot(1,1,1)
axes.set_xlabel("time $t$")
axes.set_ylabel("position $x$")
axes.set_title("$\\rho=" + str(rho) + "$, $a=" + str(a) + "$")
for i in range(carNum):
axes.plot(model.t_trace, model.x_v_trace[:,i], '.', markersize=3)
plt.show()
interact_manual(show_trace_ov, carNum=50, rho=widgets.FloatSlider(min=0.1,max=1.5, step=0.05, value=0.6),
a=widgets.FloatSlider(min=0.5, max=3.0, step=0.1, value=1.5),
initialize=Checkbox(value=True),max_t=(100,300))
<function __main__.show_trace_ov(carNum, rho, a, initialize, max_t)>
実験ビデオに対応する車の動きをシミュレーションによって再現してみましょう。
まずは、次のスクリプトを実行して見て下さい。次のような別ウィンドウが開けばOKです。
上の軌跡を描くプログラムと行ったり来たりしていると、表示されなくなるかもしれません。 その場合は、メニューの「カーネル(kernel)」→ 「再起動(restart)」をしてみてください。
アニメーション作成にはmatplotlibに備わっているanimationというライブラリを用いています。パラメータを入力するGUIを作るのは簡単ではないので、プログラムの初めのところに埋め込みます。(4~6行目)
アニメーションは、静止画を連続的に同じ画面に表示することにより動いているように見せかけるものです。36行目のframe数分だけintervalミリ秒間隔で表示します。速すぎるようであればintervalを長くしてみてください。repeatをTrueにするとエンドレスで繰り返し表示されます。
"""
OVモデルのアニメーション表示 (円形の道路上を車が移動する)
新しいウィンドウが開かないときは、FileメニューからNew Notebookを開き、
上の「OVモデルの本体」と書かれたセルと、このセルをコピーして実行してみてください。
違うノートブック間のコピー&ペーストは、ブラウザのコピー、ペースト機能を使ってください。
(jupyterのメニューにあるコピー、ペーストは同じノートブックないだけで機能します。)
"""
import matplotlib.pyplot as plt
from matplotlib import animation
%matplotlib nbagg
carNum=50
rho=0.5
a=1.2
L=carNum/rho
model = ov_model(carNum, L, a, 0.01, initialize=True)
# create the animation frame and execute
radius = L/np.pi/2.0
fig = plt.figure(figsize=(6,6))
axes = fig.add_subplot(1,1,1)
pt, = axes.plot([], [], "o")
frame_size = radius*1.1
axes.set_xlim((-frame_size, frame_size))
axes.set_ylim((-frame_size, frame_size))
axes.set_title('a='+ str(a)+ ', $\\rho=$'+ str(rho))
def init_anim():
pt, = axes.plot([], [], "o")
model.initialize_x_v()
return pt,
def anim_update(i):
n_steps = 20
model.set_params(L,a)
model.update_unit(n_steps, False)
arg_fac = 2.0*np.pi/L
x = radius*np.cos(model.x_v[:carNum]*arg_fac)
y = radius*np.sin(model.x_v[:carNum]*arg_fac)
pt.set_xdata(x)
pt.set_ydata(y)
return pt,
anim=animation.FuncAnimation(fig, anim_update, init_func=init_anim,
frames=3000, interval=20, blit=False, repeat=False) # framesは終了までの繰り返し数
# Set blit=False when you use the following "save" function
# anim.save('ov_anim1.mp4', fps=15, extra_args=['-vcodec', 'libx264'])
plt.show()
Jupyterを含むpythonの処理及び開発環境は複数ありますが、anacondaというパッケージがよく使われています。自分のパソコンでやってみたい人は、それをインストールしてみてください。"anaconda python"のようなキーワードで検索するとたくさんの情報が得られます。
たとえば、
https://www.python.jp/install/anaconda/index.html
を参照してください。
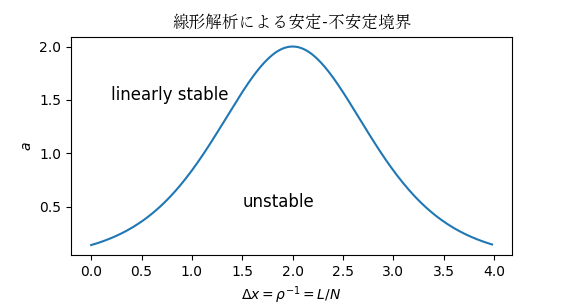
本文で説明のために使用した図を作成するプログラムを参考のために示します。関数を描画するだけのものです。なれると手軽に使えて重宝します。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib nbagg
x = np.arange(0, 4.0, 0.02)
plt.plot(x, 2./(np.cosh(x-2.0)**2))
plt.xlabel("$\Delta x = \\rho^{-1}=L/N$")
plt.ylabel("$a$")
plt.text(0.3, 1.5, "stable", fontsize=12)
plt.text(1.5, 0.5, "unstable", fontsize=12)
plt.show()
'''
最適速度関数の描画
'''
import numpy as np
import matplotlib.pyplot as plt
%matplotlib nbagg
x = np.arange(0, 8.0, 0.02)
plt.plot(x, np.tanh(x-2.0)+np.tanh(2.0))
plt.xlabel("$\Delta x$")
plt.ylabel("$V(\Delta x)$")
plt.title("$V(\Delta x) = \\tanh (\Delta x - 2.0) + \\tanh (2.0)$")
plt.show()
次のセルは、横軸に前方車との車間距離、縦軸に速度をとって車の状態を描画するプログラムです。
この図は何を物語っているのだろうか。考えてみましょう。現象をつかみやすいように台数を増やし、描画間隔を短くしてあります。14~16行目や52行目のパラメータを変更して試してみてください。(このプログラムも別ウィンドウ上に結果が表示されます。)
class ov_model_ex(ov_model):
def __init__(self, carNum, L, a, dt, initialize=True):
super().__init__(carNum, L, a, dt, initialize)
def get_headway(self):
x = self.x_v[:carNum]
x_fw = np.roll(x,-1)
delx = (x_fw- x + self.L) % self.L
return delx
import matplotlib.pyplot as plt
from matplotlib import animation
%matplotlib nbagg
carNum=200
rho=0.5
a=2.1
L=carNum/rho
model = ov_model_ex(carNum, L, a, 0.01, initialize=True)
# create the animation frame and execute
fig = plt.figure(figsize=(6,6))
axes = fig.add_subplot(1,1,1)
pt, = axes.plot([], [], "o")
axes.set_xlim((0, 4.0))
axes.set_ylim((0.0, 1.0+np.tanh(2.0)))
axes.set_title('a='+ str(a)+ ', $\\rho=$'+ str(rho))
axes.set_xlabel("$\Delta x$")
axes.set_ylabel("$v$")
# plot optimal velocity
x = np.arange(0,4.0,0.01)
y = np.tanh(x-2.0) + np.tanh(2.0)
axes.plot(x,y,"r-")
def init_anim():
pt, = axes.plot([], [], "o")
model.initialize_x_v()
return pt,
def anim_update(i):
n_steps = 20
model.set_params(L,a)
model.update_unit(n_steps, False)
arg_fac = 2.0*np.pi/L
x = model.get_headway()
y = model.x_v[carNum:]
pt.set_xdata(x)
pt.set_ydata(y)
return pt,
anim=animation.FuncAnimation(fig, anim_update, init_func=init_anim,
frames=3000, interval=10, blit=True, repeat=False)
# Set blit=False when you use the following "save" function
#anim.save('ov_anim.mp4', fps=15, extra_args=['-vcodec', 'libx264'])
plt.show()
%matplotlib inline
import numpy as np
from ipywidgets import interact, widgets
from IPython.display import clear_output, display, HTML
def show_4potential(a):
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(1,1,1)
ax.set_xlim(( -4, 4))
ax.set_ylim((-10, 10))
ax.set_xlabel("$\\phi$")
ax.set_ylabel("$f(\\phi)$")
ax.set_title("$\\phi^4$ポテンシャル $y=a \\phi^2 +\\phi^4$, a=" + str(a))
ax.grid()
x = np.linspace(-4.0,4.0,100)
y = a* x*x + x**4
ax.plot(x,y)
plt.show()
interact(show_4potential, a=widgets.FloatSlider(min=-6.0, max=2.0))
<function __main__.show_4potential(a)>