numModel

数値モデル（「微分方程式の数値解法」の応用）

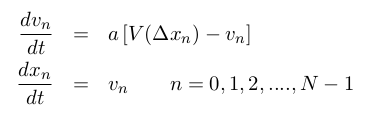
高速道路において、事故や車線規制がなくてもある程度以上混んだ状況の元で渋滞が発生することを目にしたことがあると思います。このような渋滞を自然渋滞といいます。等間隔で走行する状態が不安定になり、直線的な道路のなかに混んだところ（渋滞クラスター）と空いたところがまだらに分布している状況が出現するのです。(このページの下に実験のビデオがあります。参考にしてください。)

このような道路の自然渋滞を説明する一数理モデルを例に，モデル方程式のたて方，数値シミュレーションプログラムの作り方を実習します．

テキスト（学内のみ）

授業用情報

n変数の微分方程式である以下のような「最適速度モデル」の数値計算と視覚化プログラムを実習します。モデルについての解説は、配布テキストを使って行います。

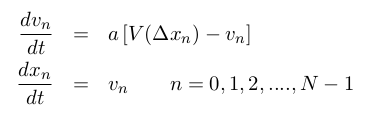
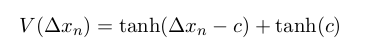
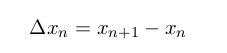
授業の進行状況に応じて、以下にコメントを付け加えていきます。

11/28 の実習

全体としては、冬休み明けまでに完成させる予定で進めます。今週は、プログラム全体の構成について理解し、チェックポイント１までを作成することを目標とします。（それができてないと、次へ進めないので、来週には、チェックポイント１までのプログラム例を示します。）

1. 課題３−４の進んだプログラム例を読んで、n変数の微分方程式に適用できるeuler()やrk4()の書き方を理解しましょう。
2. プリントの最適速度モデルの微分方程式の成り立ちを理解しましょう。
3. プログラムの流れ図をよく検討し、チェックポイント１までを行ってください。（行った内容を、e-Learningのページに報告してください。）

12/5の実習

チェックポイント１までをまず完成させ、動作を確認し、チェックポイント２にむけて進んでください。

シミュレーション本体（時間発展をルンゲクッタあるいはオイラー法で計算し，描画する）の設計とコーディングをすすめます。

印刷テキストの流れ図を参考に，以下を行なってみましょう。

• 微分方程式に対応する時間発展関数を書く。
• 微分方程式を計算するrk4あるいはeulerから上記の関数を呼び出せるようにする。
• rk4をmain関数から呼び出し，結果を表示するプログラムを書く．（とりあえず，エラーが出ないこと，1台目の車の位置と速度をprintfで書き出し，予想通りに動いているか確認するのもよい。）
  • rk4の定義は，課題３−４の発展課題とした部分の解答例を参照してもよい．
• pgplot関数を用いて描画するプログラムをmain関数内に書く。（xを与えて描画する関数を定義して，それを用いるほうが格好がよいが，描画部分はシンプルなので，本課題程度なら，main関数内に書いてもよいでしょう。）

チェックポイント１がまだの人は、こちらを参考にしてください。

チェックポイント１の時点ではマスクしておくつもりの解答例を上記の参考(プログラム例)のページに載せてしまいました。参考プログラムには、微分方程式の右辺関数の部分も載っています。これをよく読んで理解し、図示するところを作成し課題4-1を完成させてください。

• できたら、パラメータaや車の密度を変えると軌跡はどのように変化するかを確かめなさい。理論的な解析によれば、一様な状態が安定な領域と部分渋滞が起こる領域は次のように区分けされれます。(理論解析には、近似が入っているので、数値計算の結果はこれとは少し異なります。）

  

課題４−２ (12/12)

課題４−１ができたら、課題４−２に取り組んでください。

(締め切り: 12/15)

• 道路に対応する円の大きさを決め、pgplotの画面設定（座標の設定）を行う。
• 車に対応する小円を描くには、関数cpgcircを用いる。（引数は中心のx,y座標と半径)
• 動きを作るには、前の車の位置を背景色で塗りつぶし、新しい位置を自分で設定した色で書く。色の設定は、cpgsci()で行う。（引数は色を表す整数値。0は背景色）
• 中心位置 (x_draw[n],y_draw[n])は、sin(), cos()を使って、xから計算する。

   cpgsci(3);
   cpgcirc(x_draw[n], y_draw[n], 0.01);

どのように車（●）を書いたらよいか、ノートにイメージを描いてみましょう。構想ができてからプログラムにとりかかってください。

(注意:) 4-2のアニメーションは、車（●）を描き、それを下地の色で塗りつぶし、新しい位置に●を描くことの繰り返しで動いているように見せるものですが、PGPLOTでは描くごとにメモリーを消費していくので、多数回繰り返すとメモリーが足りなくなりハングアップする可能性があります。前のものをクリアするのではなくどんどん上塗りしていく仕組みになっています。

課題4-3 (12/19)

車全台の速度の平均値を計算する関数を作成し（あるいはメイン関数内に書き）、その時間変化を調べてみよう。感度パラメータ$a$や密度$\rho=N/L$の違いによりどのように変化するかをプロットしてみよう。

(締め切り: 12/27)

課題４−３の手順

(1) 課題4-2のプログラムから可視化(グラフィック)部分を取り除く

計算を速くするため、描画を行わないようにする。(コメントアウトするだけでもよいがプログラムが見にくくなるので、4-2のプログラムのコピーを別名で作成し、不必要なコードを取り除いたほうがよい。）

(2) 平均速度を計算するプログラムを書く

main関数の前に

double getAverageSpeed(double *x) {
  //
  //
}

のような平均速度を計算し、値を変えすプログラムを書く。(10行以内でかけるはず。)

(3) 一定間隔でその時刻の平均速度を計算し出力してみる

課題4-2で描画していた場所あたりで、上記の関数を呼び、時刻と平均速度をprintfで表示してみる。 たとえば、

L=160.000000, a=1.500000
100.000000, 0.963772
100.050000, 0.963771
100.100000, 0.963769
100.150000, 0.963767
 ....
199.850000, 0.964205
199.900000, 0.964199
199.950000, 0.964193
200.000000, 0.964188

(4) 計算初期の過渡的な状態を捨てて、定常的な状態の平均速度を記録

計算上限の定数と同様に、記録する時刻の下限を定義し、 GET_V_MIN < t < UpdateMaxの時間範囲の平均速度を計算の最後に密度(N/L)とともに出力する。

#define UpdateMax 200000.0
#define GET_V_MIN 100000.0

(5) それを図示してみる

次のように、ある密度$\rho=N/L$で流量$q = \rho\langle v\rangle$がピークとなり、その高密度側で、急な変化が２点でみられる。（大きな$N$の値で、長時間・多数のサンプルで平均すると、急な変化ではなく不連続な変化となって現れる。)

参考: $a=1.3$のときの、密度・流量図

補足説明

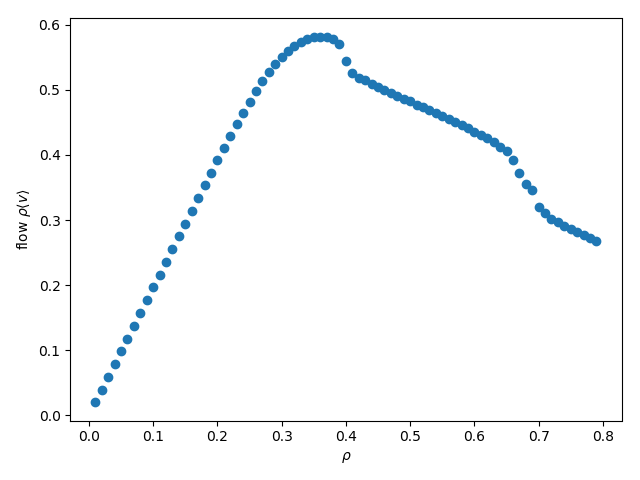
上に掲げた２つの図（理論解析の結果とシミュレーション結果）を並べてみてほしい。

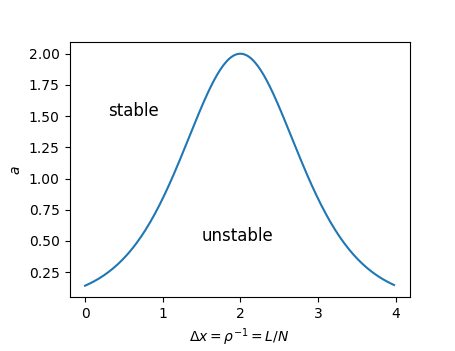
$a$を一定にして、$L$を変えてみることは左の図では水平方向に密度を少しずつずらし、平均速度と流量を計算してみると右図のようになるということである。$a=1.5$の場合、$\rho$が0.4と0.7付近、$1/\rho$では、2.5付近と1.5付近でが転移点になっている。この間の部分で部分渋滞が発生する。

シミュレーションの参考

作成するプログラムのイメージをつかむために，ブラウザ内で動作させる動作例（JavaScriptで作成）を下に掲載する．（注：感度パラメータaが V'(L/N)<a/2 では渋滞が発生，以上では起こらないことが，解析的にわかっている．下のシミュレーションでは a=2 が境目である．）

1. 軌跡の描画

2. 車の位置アニメーション

3. 実験をおこなった論文 ビデオがあるので見て欲しい．http://iopscience.iop.org/1367-2630/10/3/033001/media