初期値,境界条件が与えられれば,発展が一意的に決まるモデルを扱って来ましたが,ここでは,乱数を用いた数値計算とランダムな作用が本質的であるようなモデルについて考えます.
乱数を用いるシミュレーションでは,乱数の品質に十分注意を払う必要があります.
Visual Cに組み込まれている乱数関数はrand()です.次のページで確認できます.
http://msdn.microsoft.com/ja-jp/library/398ax69y.aspx
この関数は,0 ~ RAND_MAX (32767)の乱数を発生させますが,初期値によっては周期が短くなるなど品質がよくなく,シミュレーションに使うのには向きません. 周期だけではなく、隣り合ういくつかの数をセットにして見た場合に、一様な分布になっているかななどのチェックも必要です。
まずは、下の参考ページ1.の「2.1.4. 乱数の質の比較~特に線形合同法の欠点について」の項をみてください。授業では、このページで説明されている内容を実際にプログラムにより。試してみます。(プログラム例はこちら
そこで,最近評判のよいメルセンヌ・ツイスタ法に基づく関数の実装を利用することにしましょう.
実習では,3番目のサイトで公開している メルセンヌ・ツイスタ法のコードを利用してシミュレーションを行うことにします.
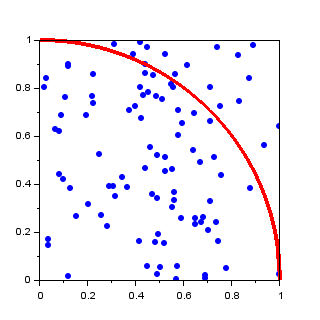
乱数による求積法を試してみよう.(0,0) - (1,1)の正方形に一様乱数を降らせて,x*x+y*y<1に入る点の割合を計算すると、円の1/4の面積つまり、π/4になるはずである。一様乱数を用いて、円周率πを求めるプログラムを作り、確かめてみよう。

x^2+y^2<1.0 なら円内の点とする.降らせた点が多いほど,π/4に近づきます。しかし、それほど効率良く近づくわけではありません。乱数を用いた数値計算法の一つとして、その振る舞いを確かめてほしい。
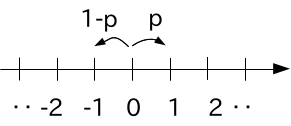
1次元ランダムウォーク(酔歩)シミュレーションを行なってみましょう. 図のように,原点から出発して,乱数を振り,確率p, 1-pで右,左に動かします.ある決まった歩数(たとえば100)の時の位置を記録します.これを多数回実施し,最後の位置の累積度数を出力します.左右均等(p=1/2)の場合についてを試してみてください.
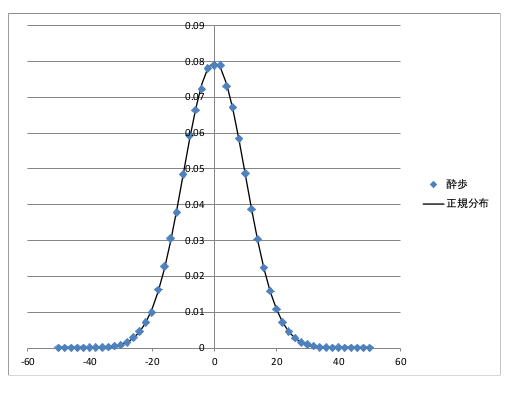
累積度数を規格化を行い(試行回数で割り相対度数にする),それを正規分布と比べてみてください.
余裕があれば、
分布関数の表示例
実習報告をe-Learningのページにアップしてください。
余裕があれば、上に挙げた乱数の解説ページ
http://www.sat.t.u-tokyo.ac.jp/~omi/random_variables_generation.html
を読んでみよう。「2.1.4 乱数の質の比較」に、3つの連続する乱数列を(x,y,z)として、鳥瞰図に表示した例が載っている。これを自分で確かめてみよう。(3次元表示は、scilabやmatlabを利用する。)
(今年は行いません.)
典型例:Isingモデル