ベイズ統計予測の概論 (Bayes Approach)

機械学習は基本的にベイズ理論をベースにしているが、ベイズではない（それ以前の）方法は「古典的確率(classical probability)」あるいは「頻度主義的(frequentist)」な確率解釈と呼ぶ。

Wikipedia: https://ja.wikipedia.org/wiki/%E3%83%99%E3%82%A4%E3%82%BA%E7%B5%B1%E8%A8%88%E5%AD%A6

下に示すような、条件付確率の概念を統計予測に適用する手法をベイズ統計予測と呼んで、素朴な頻度主義統計の考え方とは異なると解説してある記述が多いが、これがなかなかわかりにくい。前回のページと重複するが、改めて、そこを解説したい。

以下の記述は主に、「パターン認識と機械学習」（C.M. ビショップ、丸善, 原著 "Pattern Recognition and Machine Learning"）にもとづく(以下、PRMLと略す)。原著の最新情報は https://research.microsoft.com/~cmbishop/PRML/ より得られる。図表がここから得られる。以下ではそれを利用している。

PRMLの日本語版のページは、http://ibisforest.org/index.php?PRML

  • 注:
    • 頻度主義的統計やベイズ主義的統計という分類については長く議論があるようです。http://norimune.net/708　やそのページなどの引用参照
    • 前項の記事を読んだ感想： 数学的には通底するものがあり、矛盾があるわけではないが、分析対象のちがいによる結果の用い方（見方、考え方）には違いがあるし、データの分析の仕方には見方の影響があると思います。（分類に批判的なのは統計理論や数学者だというのはそのようなことに関連しているでしょう。）

条件付確率

ある事象（データ）Xが与えられたもとでのYが起こる確率$p(Y|X)$は $$ p(Y|X) = \frac{p(X|Y)p(Y)}{p(X)} $$ で与えられる。これをベイズの定理という。ただ基本はこれであるといっても、なんでそれがありがたいの？ということになるだろう。これで済まさないでほしい。

ちなみに、当たり前のような上記の分母は、Yが取りうるすべての値について確率の和をとったら1になるようにするために書いておく： $$ \sum_Y p(Y|X) = \frac{1}{p(X)}\sum_Y p(X|Y)p(Y) = 1 \quad {つまり}\quad p(X) = \sum_Y p(X|Y)p(Y) $$

あるデータ$X$が得られる前の$Y$の確率$p(Y)$を事前確率、$X$が得られたもとでの$Y$の確率$p(Y|X)$を事後確率と呼ぶ。

関数近似のベイズ予測

テストデータを用いて関数近似を行う問題、つまり、観測データから関数近似の係数を予測する問題では、$X$は観測データ$\mathcal{D}$、$Y$はフィッティング関数の係数${\bf w}$に対応させて

$$ p({\bf w}| \mathcal{D}) = \frac{p(\mathcal{D}|{\bf w})p({\bf w})}{p(\mathcal{D})} \tag{*} $$

のような意味合いになる。分母は単なる係数なので、実質的に

$$ p({\bf w}| \mathcal{D}) \propto p(\mathcal{D}|{\bf w})p({\bf w}) $$

を用いる。 また、(*)を${\bf w}$で積分すると、確率が１に規格化されているとして、 $$ p(\mathcal{D}) = \int p(\mathcal{D}|{\bf w})p({\bf w}) d{\bf w} $$ となる。これはある観測データが得られる確率を、${\bf w}$の確率に、その${\bf w}$のもとで事象$\mathcal{D}$が得られる確率をかけて積分することにより得るというのが以下のベイズ予測プロセスである。

この式に基づいてデータから係数${\bf w}$の確率分布が得る作業を行う。なお、右辺の$p(\mathcal{D}|{\bf w})$は尤度(likelihood)と呼ばれる。　補足説明

ベイズ曲線フィッティング

訓練データとして、説明変数${\bf x}=\{x_1, x_2, \dots, x_N\}$に対する目的変数の値${\bf t}=\{t_1,t_2, \cdots, t_n\}$が与えられたとき、テストデータの値$x$に対する目的変数の値$t$を推定することを行いたい。目的変数は複数でもよいのだが以下では簡単に1つとして$t$で表す。

$x$とtの関係としてはたとえばべき関数を想定すると $$ t = y(x, {\bf w}) = w_0 + w_1 x + w_2 x^2 + \cdots + w_M x^M = \sum_{j=0}^{M} w_j x^j $$ のようにかける。係数をベクトル${\bf w}^T = (w_0, w_1, \cdots, w_M)$、各べきを${\bf \phi}^T = (1, x, x^2, \cdots, x^M)$のようにあらわすと、$t={\bf w}^T{\bf \phi}(x)$のよう書くことができる。以後このような表記をする。

最小2乗法による${\bf w}$の決定は、ここでいう「古典的確率解釈」に対応する。

ベイズ統計の肝は、

  • パラメータ${\bf w}$は、分布をもつ。それは今までに得られたデータ$\{{\bf x}, t\}$ から決める。それを$p ({\bf w}| {\bf x}, t)$と書く。

  • あたらしいデータ$x$に対して、目的変数の値が$t$になる確率は $$ p(t|x, {\bf x},t) = \int p(t|x, {\bf w}) p ({\bf w}| {\bf x}, t) d{\bf w} \tag{1} $$ で与えられる。

  • データが追加されるごとに、ベイズの条件付確率の式に従って、$p ({\bf w}| {\bf x}, t)$を更新する。

ベイズ線形回帰

そのことを、PRMLの第３章「線形回帰モデル」にある図を使ってベイズ統計を線形回帰に適用する事例を説明する。

まずは、線形回帰（上記の、べき関数において、$M=1$の場合）について考える。

下の例は、サンプルデータとして、 $y=ax + b$, $a=0.5$, $b=-0.3$の周りに標準偏差$0.2$でランダムに発生させる。

線形回帰式

$$ y(x,{\bf w}) = w_0 + w_1 x $$

として、データを与えるごとに、係数${\bf w} = (w_0, w_1)^T$の確率分布がどのように変化していくかを図示したものである。

最初は何もわからないので、初期の事前分布は$w_0=w_1=0$を中心とするガウス分布としておく。（下の図の１段目の真ん中の図）

２段目右図の〇の１点が観測されたとする。その時の尤度（そのデータを生じさせた元の$(w_0, w_1)$可能性）は２段目左のようになる。与えられたデータが$(x_1,y_1)=(0.9, -0.1)$だとすると$0.9w_1 + w_0 =-0.1$、つまり$w_1 = -(1/0.9) w_0 + 1/9.$のような直線の周りのガウス分布となる。それを描いたのが２段目左の図である。

このときの事後確率は、事前確率（上の２列目）と尤度（左図）の掛け算で与えられ、２列目の図のようになる。右図は、その事後確率に基づいていくつかの直線を発生させたものである。

２つ目のデータが３段目の右図の〇のように得られたとき、その尤度は３段目左図のようになり、その前の確率に尤度をかけて事後確率を得る。

これを繰り返すと事後確率は$(0.5,-0.3)$を中心とする狭いガウス分布に収斂していく。

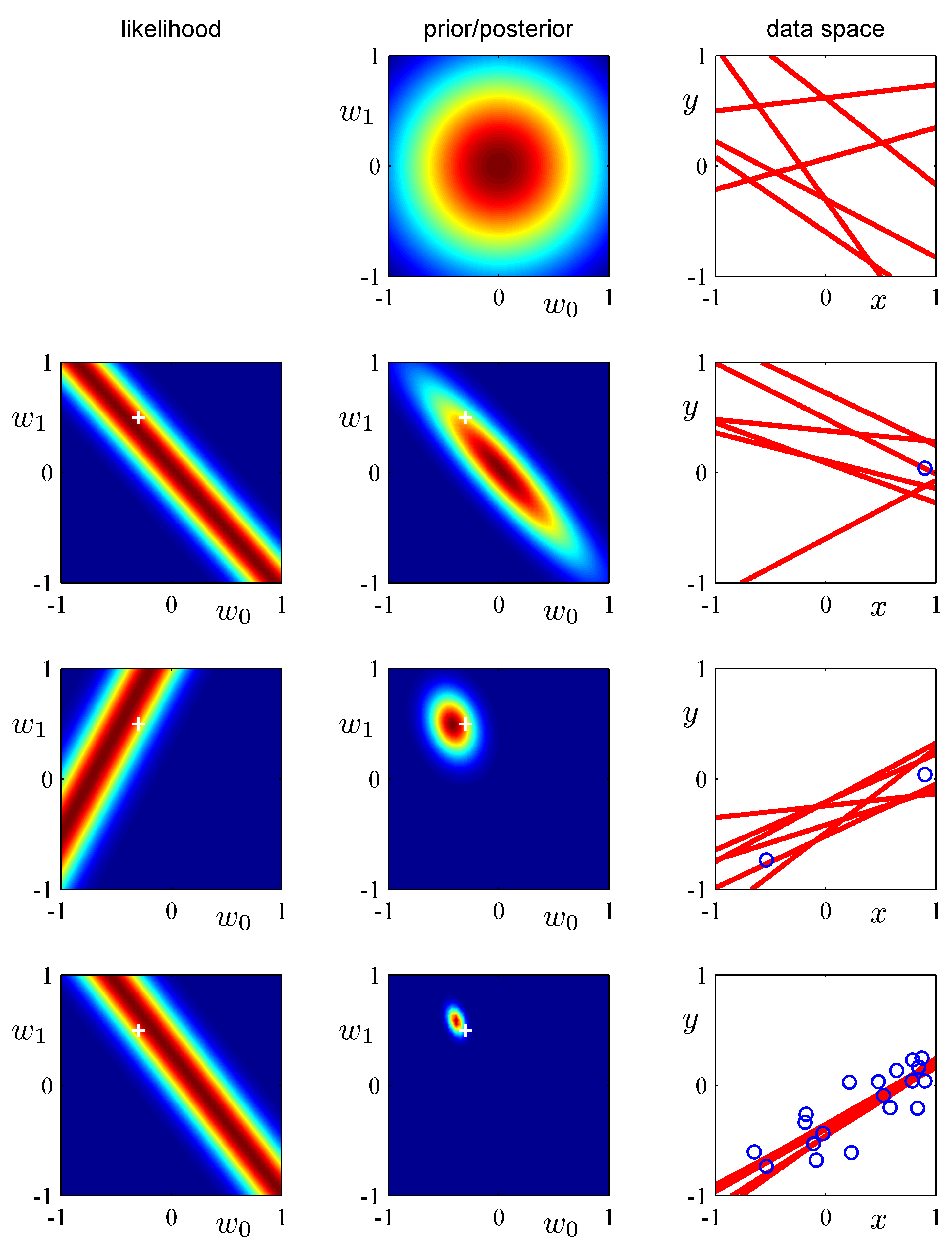
(注) 図中の"+"記号は、真の値(観測者は知らない)を表す。

説明変数が$M$個ある場合

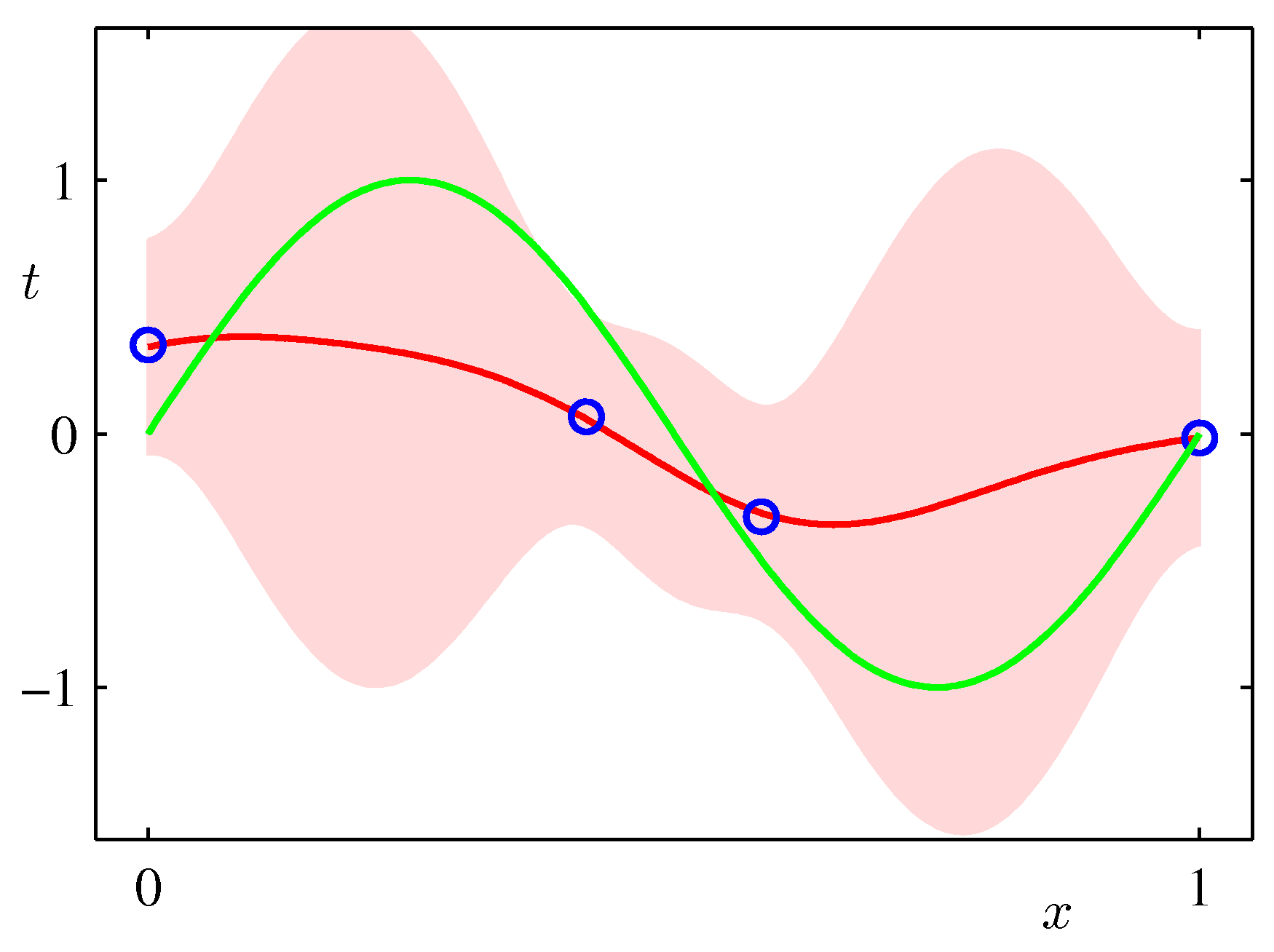
$x$値に対する目的変数の値の分布イメージ図(PRMLの図1.16): 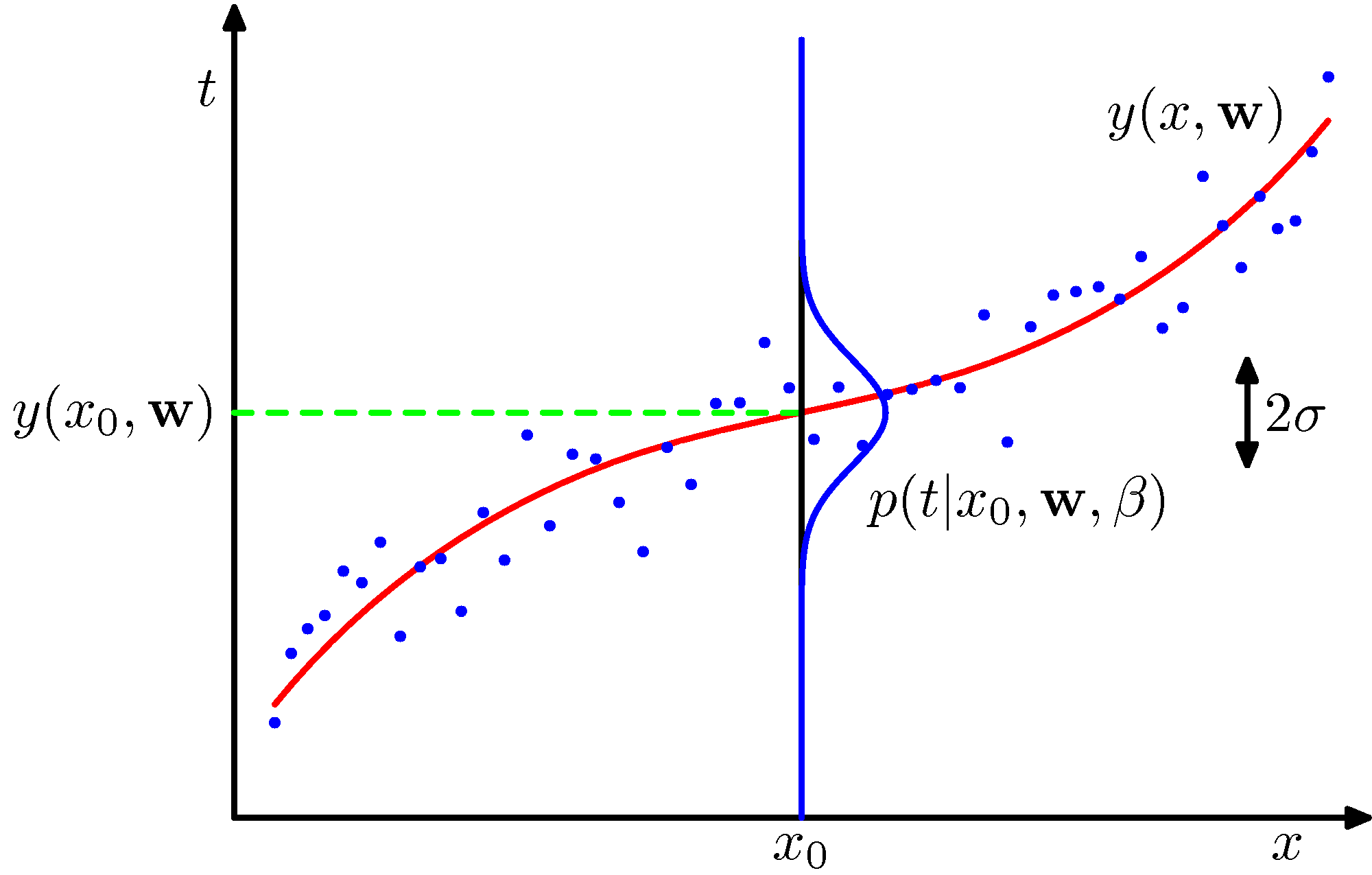この図では最尤推定値が赤の曲線（最小２乗法と同じ）で、確からしさを表す意味で、その周辺のばらつきを標準偏差$\sigma$で表している。ベイズ的アプローチでは、この$\sigma$が場所$x$によって変わることになる。

理論的な補足 (数理的な基礎を学びたい人以外はとばしてよい)

これまで、裏に潜む説明変数と目的変数の関係は多項式（べき関数）であると仮定してきたが、いつもそれが良いわけではない。ほかの関数でもよいので、それを$\{\phi_i (x)\}$ ($i=1,\cdots, M$)と書き、まとめて太字の${\bf \phi}$で表す。

$ y(\boldsymbol{x})= \sum_{i=0}^{M-1}w_i\phi_i(x) = \boldsymbol{w}^T\boldsymbol{\phi}(x) \tag{2} $

と書く。多項式の場合は、$\phi_n (x) = x^n$であり、そのほかによく用いられるものとして、ガウス関数 $\phi_n(x) = \exp [-(x - \mu_i)^2/2s^2]$や、シグモイド関数がある。

ベイズ統計推定は、目的変数の分布が、事前確率分布とデータから得られる尤度関数の積によって与えられる。

両方ともガウス分布で与えられると仮定して、データにより目的変数の推定値分布がどのように限定されていくかの説明が PRML第３章でに述べられている。

事前分布をガウシアン(平均値$0$, 分散を$\alpha$)選ぶと、${\bf w}$の事後分布もガウシアンになる（ノイズを分散$\beta$のガウス型として）。

ベイズ予測は、(1)式と同様だが $$ p(t|{\bf t},\alpha, \beta) = \int p(t|{\bf w},\beta) p ({\bf w}| {\bf t}, \alpha, \beta) d{\bf w} \tag{3} $$ 被積分関数である、$t$の条件付分布(${\bf w}$を用いて(2)式より計算される値からのずれの分布)と${\bf w}$の事後分布の両方はともにガウシアンであるので、積分の計算ができる。

導出過程を省略するが、$t$の推定からのずれ分布は $$ p(t|{\bf w},\beta) = \mathcal{N} (t| y({\bf x}, {\bf w}, \beta^{-1}) $$

また、${\bf w}$の事後分布は $p ({\bf w}| {\bf t}, \alpha, \beta)$の平均と分散は $$ {\bf m}_N = \beta {\bf S}_N {\bf \Phi}^T {\bf t},\quad {\bf S}_N = (\alpha {\bf I} + \beta {\bf \Phi}^T {\bf \Phi})^{-1} \tag{4} $$ で与えられる。

$\alpha$, $\beta$はモデルに外から与えるパラメータである。$\alpha$は、なにもデータが得られてない段階の${\bf w}$の確率の分散、$\beta$は目的変数の分散（これは観測者にとってはわからない）を表す。

これらを用いて、(3)の積分を実行すると 目的変数$t$の分布は次のようなガウシアンになる。 $$ p(t|x, {\bf x},{\bf t}) = \mathcal{N}(t| m_N, s_N^2(x)) \tag{5} $$ ここで、予測分布の平均は $$ m_N = {\bf m}_N^T \phi (x) = = \beta \phi (x)^T {\bf S}_N \sum_{n=1}^N \phi (x_n) t_n \tag{6} $$ 分散は $$ \sigma_N^2 = \beta^{-1} + \phi (x)^T {\bf S}_N \phi (x) \tag{7} $$ で与えられる。

ベイズ推計の図的理解

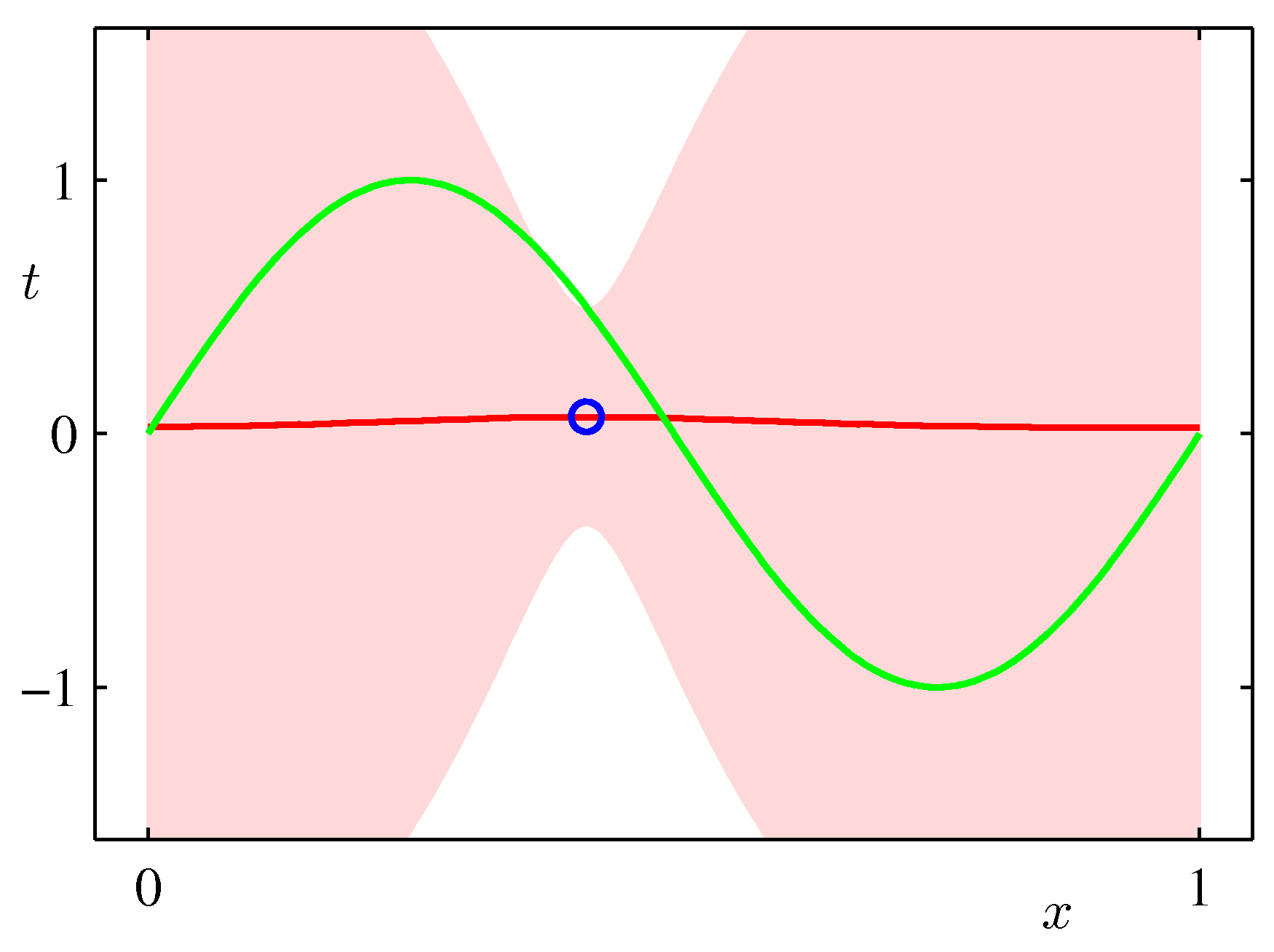
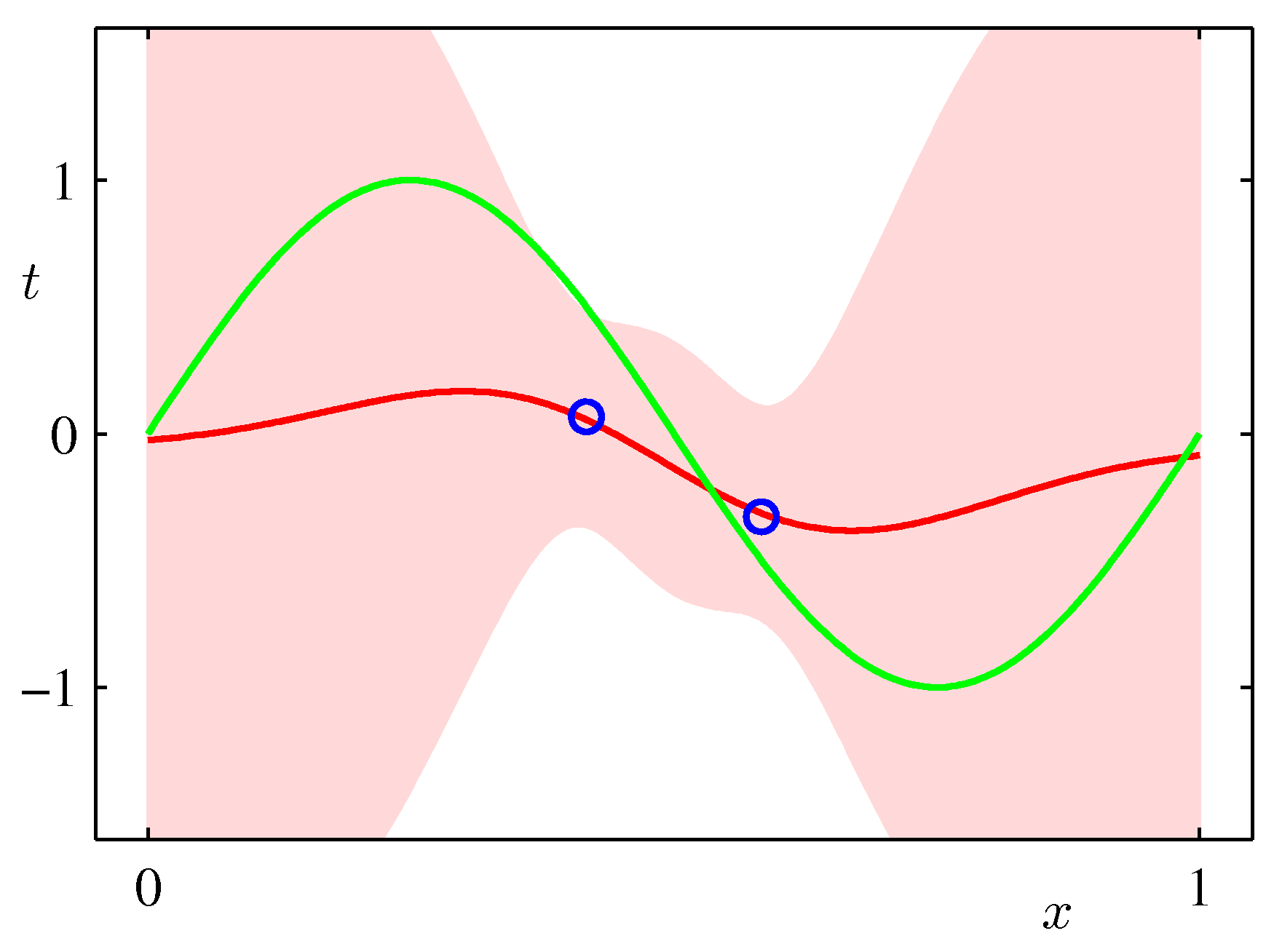
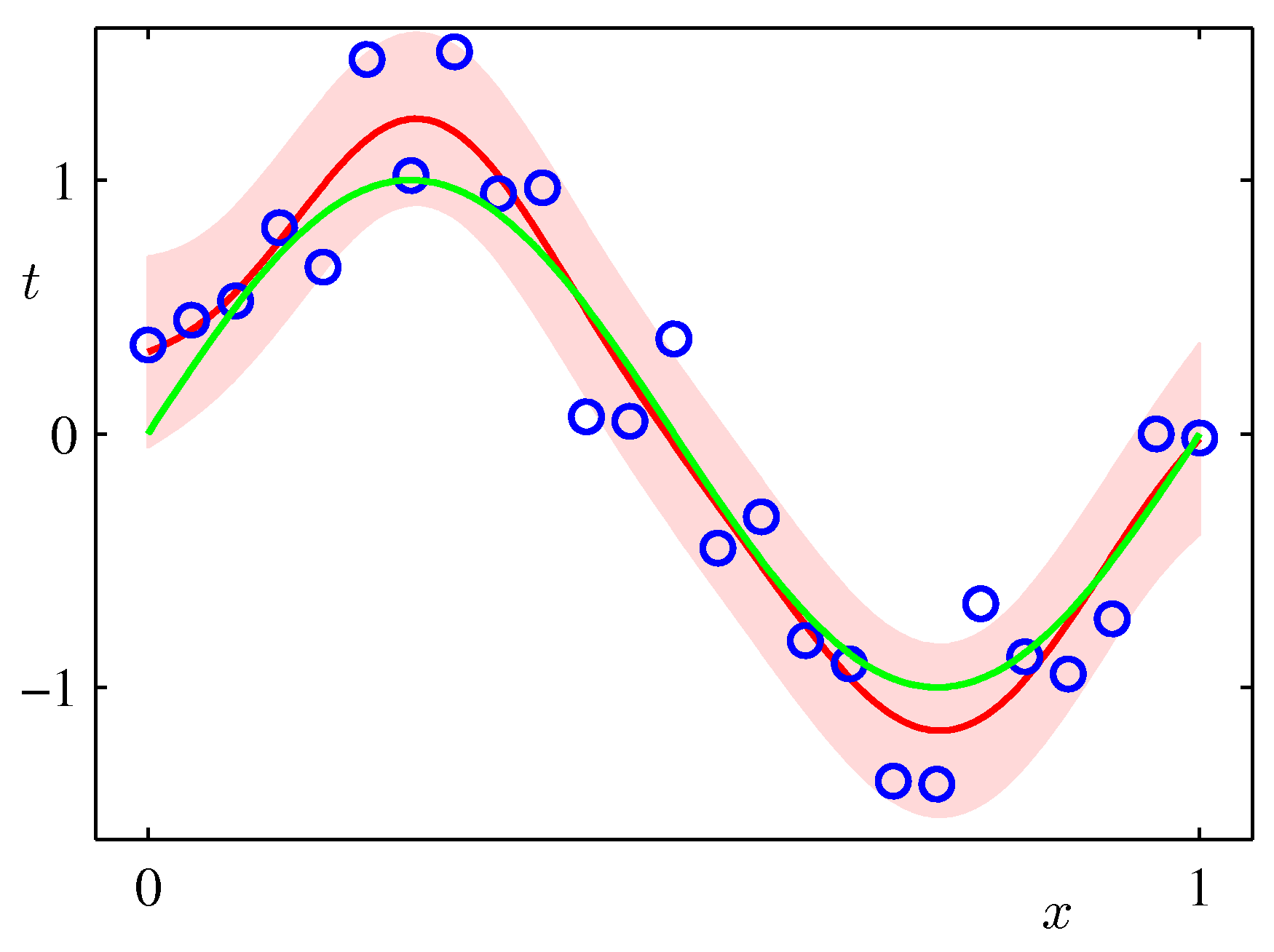
上記の数式に基づいて、データから$m(x)$と$s(x)$を計算し、$m(x)$を赤の実線で、標準偏差の範囲をピンク地で表した図の例を示す（RRMLテキストの３章）。データが増えるにしたがって推定の範囲が狭くなっていく様子がわかる。

推定の図示プログラム

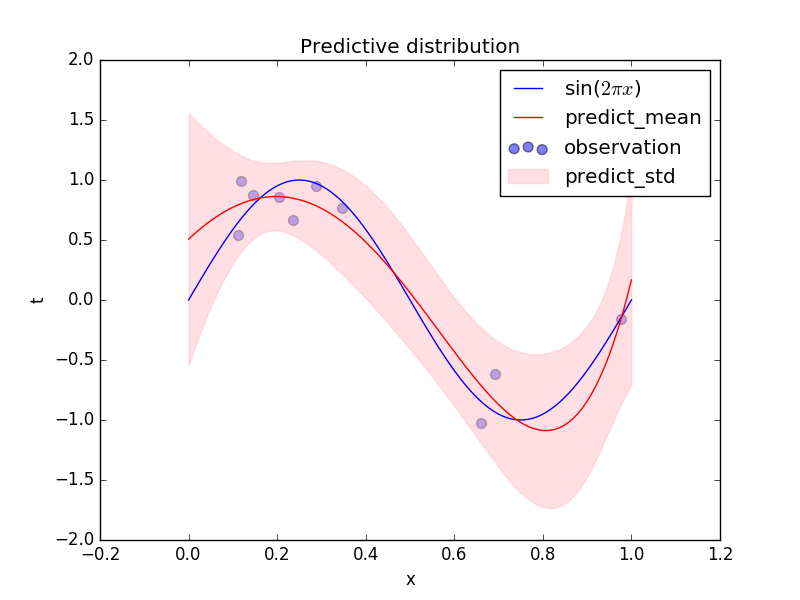
これを実際に行ってみるプログラムと結果が

https://qiita.com/ctgk/items/555802600638f41b40c5

にあるのでみてほしい。データが多い$x$の値のところでは偏差の幅が小さくなっており、値がないところは広がっていることに注意してほしい。なお尤もらしい値（ベイズでは最尤解）は、この場合は、最小2乗法の結果と一致する。

予測の中心（最も確率が高いところ）は各$x$での平均値$m(x)$で、幅（標準偏差）は$s(x)$で与えられる。上の図の青線の分布が、平均値$m(x)$、分散$s^2(x)$のガウス分布になっており、分散が場所$x$によって変化していることがわかる。

PRML_chap1example

このように、データが得られるごとに推定（目的変数の確率分布）がどんどん変化していくことがベイズ推論（ベイズ統計）らしさである。

ここでは$M$次べき関数を用いて（これをモデルの選択という）フィッティングを行ったが、モデルの選択自体もデータから推定するいろいろな方法が開発されている。(図では$M=5$。)

さらに、いつも分布がガウス分布とは限らない。２項分布やポアソン分布と考えるべき対象もある。それも使う人の選択にゆだねられる。

基底関数を説明変数$x$の「べき」でなく、ガウス基底としたPRMLに載っている図の再現は、https://qiita.com/naoya_t/items/80ea108cebc694f5cd63　にある。

また、基底を特定することなく、確からしい曲線の範囲（上のピンクの帯）をデータから求める方法もある。その一つとしてカーネル法というのがあり、そのなかでも有力な方法がSVRである。（後述）

演習問題

Web上に公開されているプログラム例

を参考に両方の基底による推定を図示するプログラムを

https://8tops.yamanashi.ac.jp/~toyoki/lectures/simulationMethods/prml3.3.html

に置いてあるので、データ数や基底の取り方によって予測がどのように変わるかを試してみよう。サンプルデータを作る関数やデータの個数を変えてみるとよい。

補足：等価カーネル

ここで扱った事後分布や誤差分布がガウシアンになる場合は、説明変数$x$に対する予測値は、事後分布の平均値(6)式のように $$ y(x, {\bf m}_N) = {\bf m}_N^T {\bf \phi} (x) = \sum_{n=1}^N \beta {\bf \phi}^T(x){\bf S}_N {\bf \phi}(x_n)t_n $$ で与えられる。

これを $$ y (x, {\bf m}_N) = \sum_{n=1}^{N} k(x, x_n) t_n \qquad k(x,x') = \beta {\bf \phi}^T(x){\bf S}_N {\bf \phi}(x') $$ と書いたとき、$k(x,x')$を、平滑化行列(smoother matrix)あるいは等価カーネル(equivalent kernel)と呼ぶ。

より進んだサポートベクトル回帰(SVR)では、この等価カーネルが大きな役割を果たすことになる。SVRでは、$\phi (x)$を設定することなく、トレーニングにより、カーネル自体$k(x,x')$を決定することになる。

In [ ]: