4. Numerical models of spatio-temporal self-organization -- a model described by partial differential equation --¶

時間空間的にマクロな構造が現れる事例と、それらに対する微分方程式モデルについて説明する。

Oregonator: a wellknown model for Belousov-Dhabotinsky Chemical Reaction¶

全過程は， $$ {\rm 2 BrO_3^- + 3 CH_2 (COOH)_2 + 2H^+ \rightarrow 2BrCH(COOH)_2 + 3CO_2 + 4H_2O } $$

この過程は3つの主な過程からなっている．（臭素酸${\rm BrO_3^-}$によるマロン酸${\rm CH_2(COOH)_2}$の酸化反応）

I. ${\rm BrO_3^-}$から${\rm Br_2}$の生成 $$ {\rm BrO_3^- + Br^- +2H^+} \rightarrow {\rm HBrO_2 + HOBr} $$ $$ {\rm HBrO_2 + Br^- + H^+} \rightarrow {\rm 2HOBr} $$ $$ {\rm HOBr + Br^- + H^+} \rightarrow {\rm Br_2 + H_2O} \qquad (1) $$

II. 自己触媒過程を経由した${\rm Br}_2$の生成 $$ {\rm BrO_3^- + HBrO_2 + H^+} \rightarrow {\rm 2BrO_2 + H_2O} $$ $$ {\rm BrO_2 + Ce^{3+} + H^+} \rightarrow {\rm HBrO_2 + Ce^{4+}} $$

この2つの反応をまとめると $$ {\rm BrO_3^- + HBrO_2 + 2Ce^{3+} + 3H^+} \rightarrow {\rm 2HBrO_2 + 2Ce^{4+} + H_2O} $$

書かれることから，${\rm Ce^{3+}}$の作用により${\rm HBrO_2}$が増える(自己触媒)過程であることがわかる．さらに${\rm HBrO_2}$は

$$ {\rm 2HBrO_2} \rightarrow {\rm BrO_3^- + HOBr + H^+ } \qquad (2) $$

によって${\rm HOBr}$に変化し，それが(1)に使われて${\rm Br_2}$が生成される．

III. ${\rm Br^-}$の生成 $$ {\rm Br_2 + CH_2(COOH)_2 } \rightarrow {\rm BrCH(COOH)_2 + Br^- + H^+} $$ $$ {\rm BrCH(COOH)_2 + 4Ce^{4+} + 2H_2O } \rightarrow {\rm 4Ce^{3+} + Br^- + HCOOH + 2CO_2 + 5H^+ } $$ $$ {\rm CH_2 (COOH)_2 + 6Ce^{4+} + 2H_2O } \rightarrow {\rm 6Ce^{3+} + HCOOH + 2CO_2 + 5H^+ } $$ $$ {\rm Br_2 + HCOOH} \rightarrow {\rm 2Br^- + CO_2 + 2H^+ } $$

反応の「振動」はつぎのように理解できる．

I.では${\rm Br^-}$が消費される．これが少なくなるとI.が起こらなくなる．
I.の2行目での${\rm HBrO_2}$の消費が起こらない一方，II.の自己触媒反応で${\rm HBrO_2}$が急増するそうすると(2) 式が活発になり，次いで，残っていた小量の${\rm Br^-}$を使って (1)が起こり，${\rm Br_2}$が生成される．
III.の過程で${\rm Br_2}$が${\rm Br^-}$に変化し，再びI.が起こるようになる．

この繰り返しが持続すると考えられる．

この説明には太田隆夫著「非平衡系の物理学」(裳華房)を参考にした。

Experiments which can be seen on Web¶

リズムの出現 https://www.youtube.com/watch?v=BZWEo1mOBSA

スパイラルパターンとターゲットパターンの出現

https://www.youtube.com/watch?v=GEF_NtTNeMc

その他にも"BZ反応"などで検索するとたくさん実験例がみつかる。

Differential Equation for Oregonator¶

化学反応の時間発展を記述した微分方程式は、ある条件を満たした時に振動が現れることが示されている。（ここではこれには立ち入らない。）

代わって、非線形振動方程式が平面的にたくさんつながった場合を考えてみる。

一列にならんだ複素振動子を$\psi_1, \psi_2, \psi_3, \cdots$としよう。お互いが自分の振動に引きこもうとする効果は $$ \frac{d \psi_i}{dt} = f(\psi_i) + D(\psi_{i+1} -\psi_i) + D(\psi_{i-1} - \psi_i) $$ のように書かれるであろう。これを連続化する。つまり、$\psi_i$を$\psi(x,t)$とすると、相互作用項は２階の空間微分に置き換わる。こうして、次のような偏微分方程式が得られる。

$$ \frac{\partial \psi}{\partial t} = (1 + ic_0) \psi - (1+ ic_2)|\psi |^2\psi + (1 +ic_1) \frac{\partial^2 \psi}{\partial x^2} $$

複素係数が大きい場合、それだけを残すと $$ -i\frac{\partial \psi}{\partial t} = c_0 \psi - c_2 |\psi|^2 \psi + c_1 \frac{\partial^2 \psi}{\partial x^2} $$ となり、これは非線形シュレディンガー方程式と呼ばれる。高次元のとき、空間微分はラプラシアンで表すことになる。

つぎでは、この方程式を数値計算してみる。

Numerical Calculation and Visualization of Nonlinear Schrodinger Equation¶

スライドとして表示するときに見やすいようにいくつかに区切ってコードを説明する。

（注）１次元のプログラムでは、変数名をpsiとしていたがここではx,y書いてある。

import libraries and variables¶

animationライブラリを利用
x,yは複素数の２次元配列
amp, diff, crgbも２次元配列、最初の２つは偏微分方程式解法用、後のは描画用

描画用のバックエンドグラフィックライブラリがうまく動いてくれない場合があるようだ。次のスクリプトの先頭に"%matplotlib qt"あるいはqtの代わりに"auto"を入れてみる。inline表示を使ってた場合、それが引き継がれてしまうとうまくいかないようだ。(qtライブラリはqt5ではうまくいかないかもしれない。その場合はqt4にダウングレードしてみる。）

%matplotlib auto
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import animation

size = 128
amp = np.zeros((size, size))    # used in the computing process as amplitudes
diff = np.array(amp, dtype=np.complex128)   # used as the Laplacian term
crgb = np.array(amp, dtype=np.float64)          # for plot

x = np.random.rand(size, size)
x = np.array(x, dtype=np.complex128)
y = np.array(x, dtype=np.complex128)

Using matplotlib backend: Qt4Agg

Constants and Initial Condition¶

# parameters of the differential equation
c1 = -1.0
c2 = 0.6
Di = 1.0  + c1*1.0j
ci = 1.0 + c2*1.0j

# initial configuration
for n in range(size):
    for m in range(size):
        x[n,m] = 0.2*(np.random.rand() -0.5 + (np.random.random() - 0.5)* 1.0j)

Define the function for the partial differential equation¶

２次元配列の各要素の計算を２重の繰り返し文で書くのではなく、行列要素の計算とするところが肝心

計算の主要部分はコンパイルされたpythonの行列計算ライブラリを利用することにより計算が１桁以上速くなる。

$\nabla^2 x$を単純差分で表すと $$ x_{n+1,n} + x_{n-1,n} + x_{n,n+1} + x_{n,n-1} - 4x_{n,n} $$ となる。これらをfor文で書くのではなく配列の一部分を切り出す記法を用いて、行列の和差をライブラリに任せることにする。x_inは0からn+1までの(n+2)x(n+2)行列である場合、 x_in[1:-1, 1:-1]は、1列からn列、1行からn行までのn行n列の部分行列をあらわす。したがって下のコードのように書けば、(1,1)から(n,n)までのn行n列についての上記差分表現の計算をまとめて行えることになる。（一番下の図参照）

（注) x_in[0,-1]は0行n+1列の要素をあらわすが、部分配列（スライスという）表記中の-1は一つ前、つまりnを表すことに注意。最後まではx_in[1:,j]のようにコロンのあとに何も書かない。

def updateField(x_in, x_out, ci=1 + 0.6j, Di= 1 -1.0j): 
    DT = 0.01 # time step
    amp = np.absolute(x_in)
    amp = np.power(amp,2)
    diff[1:-1, 1:-1] = x_in[0:-2, 1:-1] + x_in[2:, 1:-1] + x_in[1:-1, 0:-2]  + x_in[1:-1, 2:] \
                       - 4.0* x_in[1:-1, 1:-1]
    x_out[1:-1,1:-1] = x_in[1:-1, 1:-1] + DT*(1.0 - ci* amp[1:-1, 1:-1])*x_in[1:-1, 1:-1] \
                       + DT* Di * diff[1:-1, 1:-1]
    
    x_out[0, 1:-2] = x_out[-2, 1:-2]  # periodic boundary condition
    x_out[1:-1, 0] = x_out[1:-1,-2]
    x_out[-1, 1:-1] = x_out[1, 1:-1]
    x_out[1:-1, -1] = x_out[1:-1, 1]
    x_out[0, 0] = x_out[-2,-2]
    x_out[0, -1] = x_out[-2, 1]
    x_out[-1, 0] = x_out[1, -2]
    x_out[-1, -1] = x_out[1, 1]

Define animation function¶

crgbは、複素変数x (方程式の$\psi$)の位相角とし、その大きさを描画関数imshowで虹色で表現する。

def animate(i):
    global x, y, ci, Di, size
    
    # integration
    for count in range(20):
        updateField(x, y, ci, Di)
        updateField(y, x, ci, Di)
    
    # update data for plotting
    crgb =  np.angle(x)
    im.set_array(crgb)
    return [im]

Execute the calculation¶

別ウィンドウに描画面(fig)を生成し、そこに動画を描く。

コメントになっている行を生かすと、動画をmpeg4やmoving gif形式のファイルに出力できる。（ただし、情報処理教室のコンピュータには、そのためのツールがインストールされていないのでできない！）

%matplotlib auto
fig = plt.figure()
crgb = np.angle(x)
im = plt.imshow(crgb)
plt.title("c1=" + str(c1) + ", c2=" + str(c2))

anim = animation.FuncAnimation(fig, animate,
                               frames=1000, interval=10)

# anim.save('ctdgl2d.c1_1.0_c2_0.6.mp4', fps=15, extra_args=['-vcodec', 'libx264'])
# anim.save('oscillator_xyz_t.gif', writer='imagemagick',  fps=30)
plt.show()

appendix: effective calculation using python modules¶

よく知られていることだが、スクリプト言語の実行速度はコンパイル言語に比べてはるかに遅い。大量の計算を要する部分はできるだけ最適化されたモジュールを利用すべきである。

以下に、行列計算の実行速度(elapse time)比較の例を示す。(より正確な処理時間測定にはtimeitモジュールを使う。）

もう少し詳しい例はこちら

# iteration by script
import numpy as np
from numpy.random import rand
import time

N = 200
a = np.array(rand(N, N))
b = np.array(rand(N, N))
c = np.zeros((N,N))

start = time.clock()

for i in range(N):
    for j in range(N):
        for k in range(N):
            c[i][j] = a[i][k] * b[k][j]

print ("time module   :処理時間: " +str(time.clock() - start) + "\n"    )

time module   :処理時間: 5.838767

start = time.clock()

c = np.dot(a, b)

print ("time module   :処理時間: "+ str(time.clock() - start) + "\n"    )

time module   :処理時間: 0.007322999999999524

numpyの配列のインデックスについての注意¶

マイナス記号を用いて要素を取り出すときと部分配列を取り出す(slicing)ときとでは意味が異なる。

a = np.arange(10)
print(a)
print(a[-1])
print(a[5:])
print(a[5:-1])

[0 1 2 3 4 5 6 7 8 9]
9
[5 6 7 8 9]
[5 6 7 8]

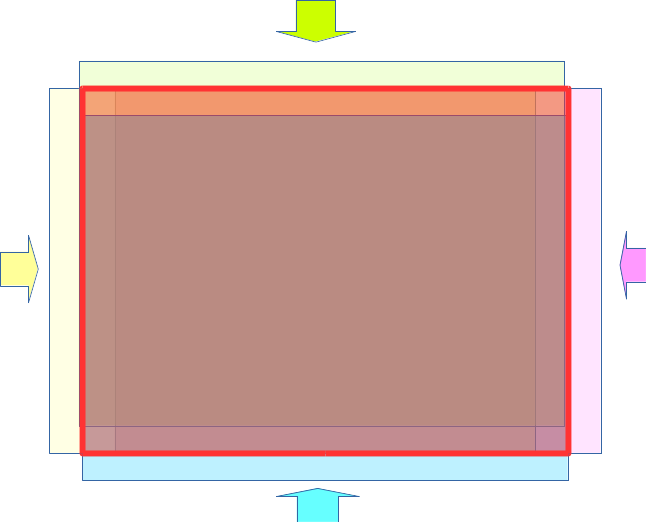
simple difference representation of Laplacian¶

Laplacianの離散化版

文字式で表すと

$$ x_{n+1,n} + x_{n-1,n} + x_{n,n+1} + x_{n,n-1} - 4x_{n,n} $$

pythonプログラムでは

x_in[0:-2, 1:-1] + x_in[2:, 1:-1] + x_in[1:-1, 0:-2] + x_in[1:-1, 2:] - 4.0* x_in[1:-1, 1:-1]

に関する説明図

$(N+2)\times(N+2)$の配列のうち、図のような$N\times N$の部分を切り出して重ね、ずらした４枚の各セルの値から中心のセルの値の４倍を引く操作がLaplacianになる。 (黄色、マゼンタ、シアン、グリーンが第１項～４項に対応）