下の例では,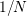 以上であれば,Cが増殖することになる.そうなる条件は素朴な考察から
以上であれば,Cが増殖することになる.そうなる条件は素朴な考察から
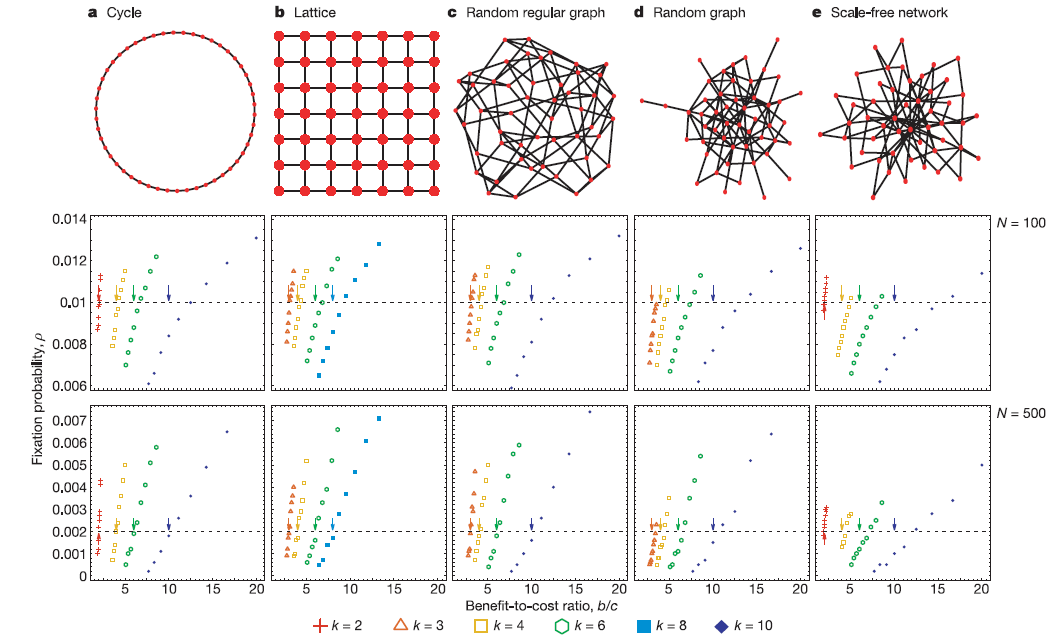
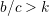 が得られる.これは下図に示すように,規則的なネットワークでは完全に再現される.スケールフリーネットでもだいたい当っている.
が得られる.これは下図に示すように,規則的なネットワークでは完全に再現される.スケールフリーネットでもだいたい当っている.
"Cooperation Prevails When Individuals Adjust Their Social Ties"
(F.C. Santos, J.M. Pacheco andT. Lenaerts, PLOS Comp. Biol. 2, 1284 (2006))
これまでのモデルは固定的なネット上のエージェントの戦略(strategy)に対するダイナミクスであったが,ネット自体も動的にしたモデルを考えている.
結果
リンク換えの頻度が大きい( W 大)ほど,Cの割合が増える.
"Cooperation, social networks, and the emergence of leadership in a prisoner's dilemma with adaptive local interactions" (もうひとつのネットワークつなぎ変えを含むモデル)
(Martin G. Zimmermann and Victor M. Eguiluz, PRE 72, 056118 (2005))
モデル
i サイトの状態を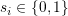 とする.1がcooperatorをあらわす.
とする.1がcooperatorをあらわす.
ふつうのreplicator dynamics
- Payoffの値
-
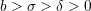
- ステップ1(payoffの計算)
-
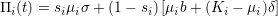
ここで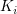 は i の次数,
は i の次数,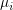 は最近接ノードの数.
は最近接ノードの数.
- ステップ2 (戦略の更新)
-
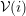 を i の最近接ノードの集合とする.
を i の最近接ノードの集合とする.
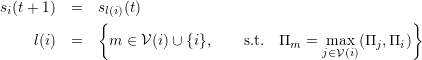
- ステップ3(つなぎ変え)
-
i が不満な場合(
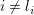 )のみ,確率 p でつなぎ変えがおこる.もし, i が D ならば,近傍の一つの D と関係を切り,他のノードからランダムに選んだノードにつなぎ変える.ただし,自分へのリンクや2重リンクにはならないようにする.
)のみ,確率 p でつなぎ変えがおこる.もし, i が D ならば,近傍の一つの D と関係を切り,他のノードからランダムに選んだノードにつなぎ変える.ただし,自分へのリンクや2重リンクにはならないようにする.
i が C の場合は,つなぎ変えをしない. C は保守的であり自発的なつなぎ変えインセンティブをもたないと考える.他からのつなぎ変えは受け入れる.(行動的なC, 公共的行動の伝道者はいてもいいのでは.)
結果
協力行動の拡大
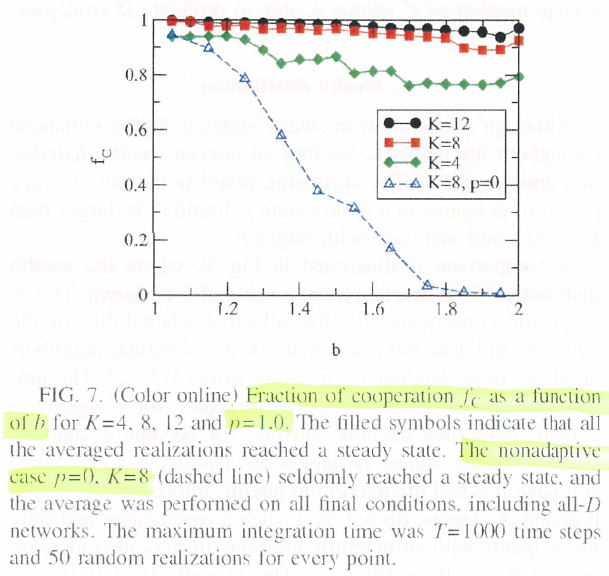
- 誘惑の利得bと平均次数Kをパラメータとして調べた.平衡状態でのCの割合を
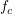 と書く.
と書く.
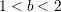 の範囲で,どの値でも(初期状態によるが)
の範囲で,どの値でも(初期状態によるが)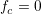 の状態は出現する.
の状態は出現する.- b が大きくなるとともに
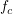 は小さくなる.
は小さくなる.
- 組み替え(adaptation)の確率が大きいと,Cは生き残りやすい. p が有限でも小さいと,平衡状態に近づくのに時間がかかる.
- 同じ b に対して,Kが大きいほど,
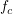 が大きい.(K=4,8,12について調べている.
が大きい.(K=4,8,12について調べている.
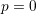 (nonadaptive case)では,
(nonadaptive case)では,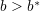 では,初期に一つでもDがいれば,すべてDになる状態が安定である.K=8,
では,初期に一つでもDがいれば,すべてDになる状態が安定である.K=8, 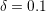 では,
では,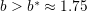 .
.
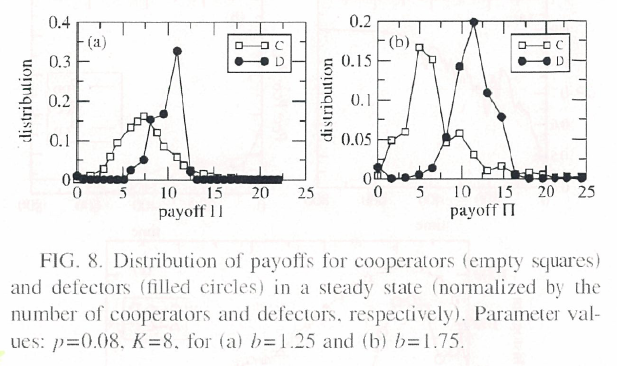
富の分配
CとDの利得の分布をみた.
- 分布関数のピーク位置も平均値もDの方が大きい.これは固定的なネットワークではおきない現象である.
- Dは,利得向上のために頻繁につなぎかえを行う.Cとつながり,利用しようとする.(利にさとい)
- 全体として,Cは増殖することが可能であるが,その場合でも全体としてはDに比べて貧しい.
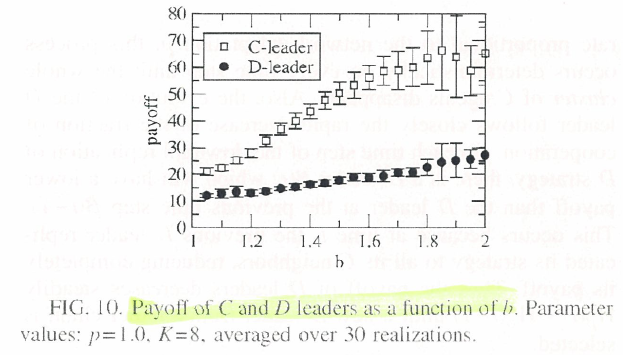
リーダーと協力的エージェントのクラスタ
- たくさんのエージェントとつながっていれば累積利得は大きいから,そのようなCは戦略を変化させることなく存在し続け,それにつながりをつけたDは,その利得を学んでCに変化する.結果として,Cのリーダーはリンクを集め,さらに利得が増える.
- その傾向は, b が大きいほど顕著である. b が小さいときは,小リーダーが「乱立」.大きい b では,最大のリーダーが「一人勝ち」.
- あるとき,Cのカスケードチェーンに属する上中位のCが他からつながってきたDにより改心させられたとき,そのカスケードチェーンをつたってDが増殖することがある.そのような雪崩現象により,
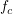 は時間とともに振動する.Dリーダーは,しかし,まわりにCがいなくなるにつれ利得が減少する(新しいDリーダーからリンクがはられるまでは).
は時間とともに振動する.Dリーダーは,しかし,まわりにCがいなくなるにつれ利得が減少する(新しいDリーダーからリンクがはられるまでは).
- 振動の回数は有限でおさまる.
(C及びDそれぞれのノードのうちの最大利得を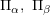 とする.)
とする.)
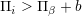 をもつ富裕なCがあると,Dのチェーンを吸収してしまう.
をもつ富裕なCがあると,Dのチェーンを吸収してしまう.- チェーン上の利得差(payoff gap)がチェーンにそって減少しない場合,チェーンを上昇する撹乱を防ぐことができる.(Proposition 4の議論をトレースする必要あり)
「行動変容」政策への適用・問題意識
- ZE(Zimmermann & Eguiluz)の利得とは?
- リーダーはオピニオンリーダー? とすると利得は何にあたるか.
- 非常につながりの薄い場合(駅周辺の駐輪問題のような),はdefectorが闊歩しやすい? リンクは現実の何に対応するか.
- 必ずしも「つながり」によるゲームだけではないだろう.場の影響は大きいはずだ.
- 不利を承知で公共利益(ペアワイズではないもっと広い範囲の)優先という戦略をとるエージェントの存在は?
TDMと社会的ジレンマ:交通問題解消における公共心の役割
(社会的ジレンマの枠組みや,TDMにおける構造的方略と心理的方略のカテゴライズ,高次ジレンマなどのレビューを最初に行っている.)
社会的ジレンマの範疇で捉えられる交通問題のもっとも原初的なものとして「 道路ネットワークジレンマ」を
「社会的ジレンマの処方箋」
(藤井聡,ナカニシヤ出版,2003)
心理的方略
学習:事実情報提供による変容
経験誘発法:(試してみると意外とよい)
コミュニケーション("コトバ"による変容)
「社会的ジレンマの解消のために最も必要とされているのは,人々の”公共心”の活性化である.」(p.258)
その上で,課題として次の4つを挙げている.
- 社会的価値と協力行動
-
社会的な価値観と公共心,倫理性とは密接な関係があることが予想される
- より効果的な心理的方略の検討
-
例として,「定期的に同一個人と繰り返しコミュニケーションを図る」,構造的方略と心理的方略のタイムリーに組み合わせるなど
- 組織の協力行動
- 実務適用事例の蓄積
注目した点(ランダムに)
- 内的動機(倫理性?)が活性化している状態では,報酬はかえってマイナスにはたらく
- アンケートの事例 (p.189)
- 「フレイ達は"原子力発電所を受け入れることを国家として必要ならば,それを受け入れることもやぶさかではない" という形の公共心(public spirit)が,報酬の提案によって駆逐されてしまい,結果として,原子力発電所という迷惑施設を受け入れることに反対する,という人々の利己的傾向を助長してしまったと議論している.」(p.191)
ただし,内的動機(intrinsic motivation)がない場合には,補助金(補償金)は当該地域のサポート引き出すのに有効であるとフレイらは結論している.(B.S. Frey and F. Oberholzer-Gee, Am. Econ. Rev. 87 , 746 (1997))
メモ
- 心理的方略を数理モデルに取り入れるとすると,個人の行動関数(あるいはパラメータ値)が変化するということになるか
- 実証性(モデルの妥当性を何によって検証するか)
社会心理学者の一見解「日本の『安心』はなぜ消えたのか」(山岸俊男)
- 超利己的な分子を仲間外れにする.(「いじめ」問題に関わって,「自発的な秩序形成のための『排除行動』)
- 信頼の構造
- 公正性(fairness)
- 評判の力
- ネットオークションでの評判 レモン市場にならない原因は,ネガティブな評判よりポジティブな評判を評価する方向に参加者がかわっていったことにある.
- 評判には「追い出し」と「呼び込み」の2つの効果がある.
- しかし,大きさがきまった集団の構造とインターネットオークションのような構成員の大きさが変化するシステムとはメカニズムがことなることに注意が必要だろう.
The Cost of Price Incentives: An Empirical Analysis of Motivation Crowding-Out
Bruno S. Frey and Felix Oberholzer-Gee (Am. Econ. Rev. 87, 746 (1997))
補助金などprice incentiveが内在的な公共心を破壊することが(部分的にせよ)あることを,心理学的な知見に基づく数理的モデル(?)により示した論文.
例として,原発立地域における住民意思が,補助金により私利的になり,公共心が失われる例をあげている.
いわゆるデシ(Deci)理論の「住民意思」版
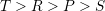
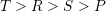
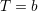
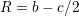
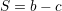
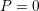
と定義できる.この r を変えたときに,協力者の存在割合がどう変化するかと協力者の空間分布がどうなるかがこの論文でのテーマ.
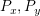 を計算.
を計算.
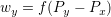 を計算し,それに基づいて状態変化させる
を計算し,それに基づいて状態変化させる
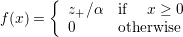
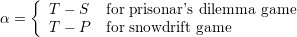
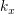 をノードxの次数とする.xの状態変化は
をノードxの次数とする.xの状態変化は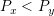 のとき,
のとき,
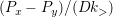
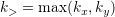 であり,PDの場合,
であり,PDの場合,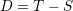 ,SGの場合,
,SGの場合,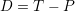 .
.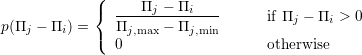
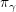 とする.(PDでは,ノードがCのときS, DのときP)
とする.(PDでは,ノードがCのときS, DのときP)
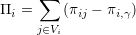
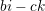 .Dの報酬は
.Dの報酬は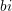 とする.つまり,Cはつながったノード全部に均等に c のcostを払い,となりのCからは b の利得(benefit)を受ける.Dはコストを払わない.(相互作用が対称でなくて良いのだろうか?)
とする.つまり,Cはつながったノード全部に均等に c のcostを払い,となりのCからは b の利得(benefit)を受ける.Dはコストを払わない.(相互作用が対称でなくて良いのだろうか?)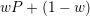 とする.
とする.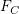 ,
, 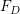 とし,対象ノードがCになる確率を
とし,対象ノードがCになる確率を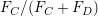 とする.
とする.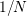 以上であれば,Cが増殖することになる.そうなる条件は素朴な考察から
以上であれば,Cが増殖することになる.そうなる条件は素朴な考察から
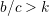 が得られる.これは下図に示すように,規則的なネットワークでは完全に再現される.スケールフリーネットでもだいたい当っている.
が得られる.これは下図に示すように,規則的なネットワークでは完全に再現される.スケールフリーネットでもだいたい当っている.

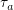 , adaptiveのa)と戦略を変えるタイムスケール(
, adaptiveのa)と戦略を変えるタイムスケール(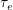 , evolutionのe)を考え,その比
, evolutionのe)を考え,その比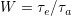 をパラメータとする.
をパラメータとする.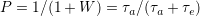 でtieの変化を,
でtieの変化を,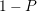 の確率で戦略の変化を行う.
の確率で戦略の変化を行う.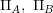 として,
として,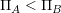 のとき次の確率でBの戦略を受け入れる.
のとき次の確率でBの戦略を受け入れる.
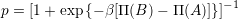
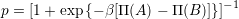 でつなぎ変えを行う.つなぎ変えの相手は,Bとリンクしているノードからランダムに選ぶ.
でつなぎ変えを行う.つなぎ変えの相手は,Bとリンクしているノードからランダムに選ぶ.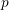 でAのつなぎ変えをし,確率
でAのつなぎ変えをし,確率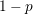 でBのつなぎ変えをする.
でBのつなぎ変えをする.

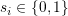 とする.1がcooperatorをあらわす.
とする.1がcooperatorをあらわす.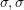
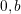
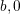
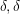
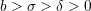
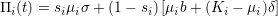
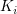 は i の次数,
は i の次数,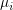 は最近接ノードの数.
は最近接ノードの数.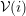 を i の最近接ノードの集合とする.
を i の最近接ノードの集合とする.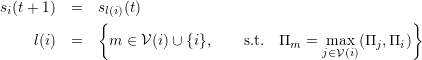
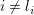 )のみ,確率 p でつなぎ変えがおこる.もし, i が D ならば,近傍の一つの D と関係を切り,他のノードからランダムに選んだノードにつなぎ変える.ただし,自分へのリンクや2重リンクにはならないようにする.
)のみ,確率 p でつなぎ変えがおこる.もし, i が D ならば,近傍の一つの D と関係を切り,他のノードからランダムに選んだノードにつなぎ変える.ただし,自分へのリンクや2重リンクにはならないようにする.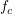 と書く.
と書く.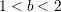 の範囲で,どの値でも(初期状態によるが)
の範囲で,どの値でも(初期状態によるが)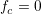 の状態は出現する.
の状態は出現する.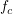 は小さくなる.
は小さくなる.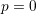 (nonadaptive case)では,
(nonadaptive case)では,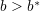 では,初期に一つでもDがいれば,すべてDになる状態が安定である.K=8,
では,初期に一つでもDがいれば,すべてDになる状態が安定である.K=8, 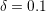 では,
では,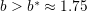 .
.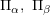 とする.)
とする.)
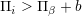 をもつ富裕なCがあると,Dのチェーンを吸収してしまう.
をもつ富裕なCがあると,Dのチェーンを吸収してしまう.