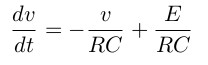
配布テキストは、e-Learningのページにもあります。 https://moodle.yamanashi.ac.jp/2016/course/view.php?id=5288#section-5
まずは、テキストのプログラム8.1を実行してみてください。テキストの実行例は「分割数」を10としていますが,これを大きく(刻みを細かく)することにより,精度は増します.そのことを確かめてください.(解析的な解は,156ページの最下行にあります.これと比較してみましょう.)
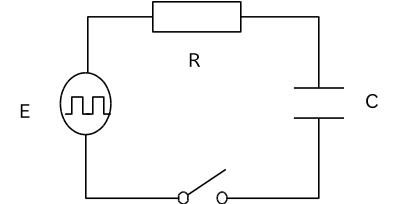
図のようなRC回路に振動数0.1Hzの方形波電圧Eを印加した時,キャパシタCの端子電圧vの変化を表す微分方程式を数値計算しなさい.
できたら,結果をcsv形式のファイルに出力し,v(t)を図示してみてください.また,いくつかのRCで計算し,結果を確かめなさい. (下の課題3−1gの参考図にあるような図になるはずです.この微分方程式は応用解析等さまざまな授業にすでに登場していますね.)

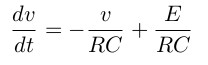
テキストのプログラム8.1のxに当たる変数は,この実習では時間をあらわし,時間発展を記述する方程式を扱うので、そのことがわかりやすいようにプログラム8.1を少し書き換えます.
以下の書き換え例を読み解き、オイラー法の関数と微分方程式に該当する関数の中身を考えなさい。
プログラム例:
/*
直列RC回路の電圧を計算する
*/
#include <stdio.h>
#include <stdlib.h>
/* 関数の定義 */
double func(double t, double x, double rc, double E);
/* オイラー法 */
void euler(double x0, double h, double t_max, double rc, double E,
double (*f)() );
int main() {
double h=0.01, x0 = 0.0, t_max = 10.0, E = 1.0, rc =2.0;
euler( 0.0, h, t_max, rc, E, func );
return 0;
}
/* オイラー法 */
void euler(double x, double h, double t_max, double rc, double E,
double (*f)() ) {
double t;
for ( t = 0. ; t < t_max ; t+=h) {
// ここにオイラー法の基本式を書く。関数fを用いる
printf(); // printfの引数も自分で考える
}
}
/* 関数の定義 */
double func(double t, double x, double rc, double E) {
// ここは各自考える
}
プリントに紹介したようにpgplotというグラフィックライブラリを使用します。ちょっと古めかしいですが、数値計算の結果をプログラム内で作図するには便利です。
プログラムのコンパイル(ビルド)のときにグラフィックライブラリをリンクする必要があります。リンクライブラリの指定をこのページに従ってセットしてください。
日本語のマニュアルとして、
http://fluidlab.1.k.u-tokyo.ac.jp/softwares/pgplot-j.html
が便利です。このページではfortranというプログラム言語で利用することを想定しています。本実習ではCからよびだすので、それぞれの関数名は頭に"C"がつきますので、その点を勘案して読んでください。
まずは、次のページにあるプログラムが実行できることを確かめてください。
ヒントを参考にして、課題3−1の結果を図示するプログラムを作成しなさい。(これを 課題3−1g とします。プリントにはありませんので、番号を3−1gとしました。)
時間があったらテキストにあるホイン法(オイラー法より精度の高い方法)で作成してみましょう。
表示例:
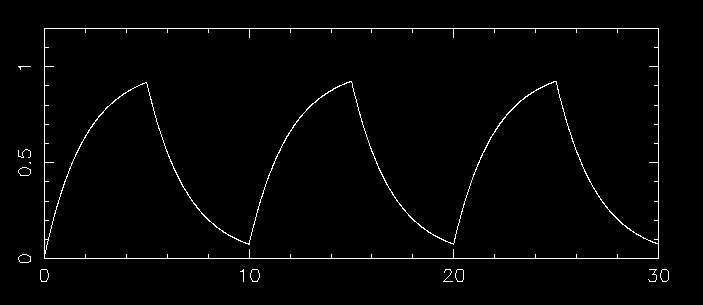
ヒント
/* RC回路の電圧を計算し、描画するプログラム */ #include <stdio.h> #include "cpgplot.h" /* 関数の定義 */ double func(double t, double x, double rc, double E); /* オイラー法 */ void euler(double x0, double h, double t_max, double rc, double E, double (*f)(double, double,double, double) ); int main(void) { double h, x0 = 0.0, t_max = 30.0, E = 1.0, rc =2.0; /* pgplotを使った描画の初期設定 */ cpgopen("/CGW"); /* windowsの場合は "/CGW", Linuxの場合は"/xserv" */ cpgpap(8.0,0.5); // グラフィック画面の横幅(インチ)と縦横比 cpgsch(2.0); // 文字の高さ cpgenv(0., t_max, 0., E*1.2, 0,0); /* 初期設定 以上 */ cpgmove(0.0, 1.0); /* 最初のペンの位置 */ euler( 0.0, h, t_max, rc, E, func ); return 0; } /* オイラー法 */ void euler(double x, double h, double t_max, double rc, double E, double (*f)() ) { double t; for ( t = 0. ; t < t_max ; t+=h) { // 前の課題と同様 cpgdraw(t,x); /* 前の位置から現在位置まで線を引く */ } } /* 関数の定義 */ double func(double t, double x, double rc, double E) { // 前の課題と同様 }
2変数の時間発展微分方程式の例としてロトカ・ボルテラ方程式を取り上げます。説明はプリントを見てください。
方程式の意味が理解できたら 課題3−2, 3−3 を行いなさい。 【締め切り:11月23日】
表示例:
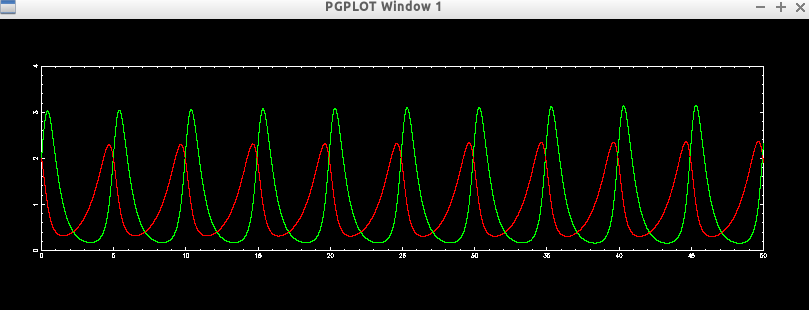
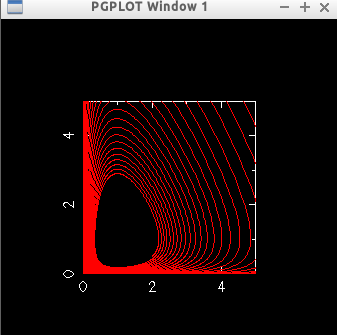
【3−2へのヒント】
#include "cpgplot.h" #include <stdlib.h> #include <math.h> #include <stdio.h> /* 関数定義 */ double func_x(double x, double y); double func_y(double x, double y, double m); void euler(double x0, double y0, double m, double h, double t_max, double (*fx)(double, double), double (*fy)(double, double, double)); /* メイン */ int main() { double x0=2.0, y0=0.5, m=2.5, t_max= 50.0, h=0.001; cpgopen("/CGW"); cpgpap(8.0,0.3); cpgenv(0.,t_max,0.0,4.0,0,0); euler(x0, y0, m, h, t_max, func_x, func_y); } /* オイラー法 */ void euler(double x0, double y0, double m, double h, double t_max, double (*fx)(double, double), double (*fy)(double, double, double)) { double x, y, t=0.0; double t0; x = x0; y = y0; t0=0.0; for (t = 0.0 ; t < t_max ; t+=h) { x0 = x; y0 =y; // 前の値x0,y0をもとにx,yを計算する //オイラー法の本体 // printfによる数値出力 cpgsci(2); // 色の設定 cpgmove(t0, x0); // (t0,x0)にペンをアップで移動 cpgdraw(t,x); // (t,x)までペンダウンで移動(線を書く) cpgsci(3); // 色の設定 cpgmove(t0, y0); // (t0,y0)にペンアップで移動 cpgdraw(t,y); // (t,y)までペンダウンで移動 t0 = t; } } /* 関数の定義 */ double func_x(double x, double y){ // xの時間微分 } double func_y(double x, double y, double m) { // yの時間微分 }
ホイン法、ルンゲ・クッタ法に関する授業での説明は配布テキストに基づいて行います。
テキストのプログラム8.2がホイン法のプログラム例です。
実際は、多くの場合、このルンゲ・クッタ法が用いられており、数値計算ライブラリにはほぼ間違いなく含まれている。
課題3−3とプログラム8.2,プログラム8.3や配布資料を参考にして、ロトカ・ボルテラ方程式を、ホイン法及びルンゲ・クッタ法により数値計算するプログラムを作成し、オイラー法での計算と比較しなさい。 (関数の仕様については、テキストのプログラム通りではなくて良い。関数の引数をどのようにするかなどノートの上で構想をねってからプログラムにとりかかること。下記「発展課題」のように汎用性のあるプログラムができるともっと良い。)
数値的に精度を確かめるために、3−3のように軌跡を描いた時の最高点の値を記録する方法を考えてみましょう。オイラー法では、周回ごとに軌道が膨れて行きましたが、ホイン法やルンゲ・クッタ法ではどうなるでしょうか。ほぼ同じ値になれば軌道は閉曲線になっていると判断できます。
【締め切り: 11/30】
上の【3−2へのヒント】では、1変数の微分方程式に関するテキストのプログラム例を2変数に対応させた。その際、微分方程式を反映させた2つの関数func_x, func_yを用いる方式をとった。
これは、わかりやすい拡張ではあるものの、3変数、4変数と変数が増えるごとに関数を増やしていく必要があり、拡張性には問題がある。
微分方程式の定義関数func()やそれを呼び出すeuler()、heun(), rk4()関数の仕様を、N変数に対応できるようにするにはどうしたら良いだろうか。
Cの関数では配列など複数の値を返すとき、return文で結果を返すのではなく、関数の引数にポインタを渡して、結果を呼び出し元で使えるようにする方法が取られる。1
余裕がある人は、その方法でのプログラムを考えてみて欲しい。具体的には、次のような方針でプログラムしてみる。
/* オイラー法 */ /* size_of_x : 変数の数 (ロトカ・ボルテラ方程式なら2) * x0: size_of_x成分の配列(入力) * x: 計算結果を入れる配列 * h: 時間刻み * f: 微分方程式の右辺の関数 (引数を通じて入力と出力をやり取りする) */ void euler(int size_of_x, double *x0, double *x, double h, void (*f)()) { } /* ルンゲ・クッタ法 */ void rk4(int size_of_x, double *x0, double *x, double h, void (*f)()) { }
// Lotka-Volterra方程式 m = 0.5; function xdot = dotFunc(t,x) // dx/dt, dy/dt関数の定義 xdot(1) = x(1) - x(1)*x(2); xdot(2) = m * (x(1)*x(2) - x(2)) endfunction t0 = 0.0 t_max = 40.0 dt = 0.01 t = t0: dt :t_max; // 時間始め、刻み、終わり x_ini = [2; 4]; // 初期値 xout = ode(x_ini, t0, t, dotFunc) clf(); // 時間変化のプロット subplot(2,1,1) plot(t,xout(1,:),"r-") plot(t,xout(2,:),"b-") // 軌跡のプロット subplot(2,1,2) plot(xout(1,:), xout(2,:)) // comet(xout(1,:), xout(2,:)) // アニメーションプロット
matlabでも同様と思うが,常微分方程式の関数名,引数の順序などが若干異なる.
% // Lotka-Volterra方程式 m = 0.5; function xdot = dotFunc(x,t) % // dx/dt, dy/dt関数の定義 m =0.5; xdot(1) = x(1) - x(1)*x(2); xdot(2) = m * (x(1)*x(2) - x(2)) endfunction t0 = 0.0 t_max = 40.0 dt = 0.01 t = t0: dt :t_max; % // 時間始め、刻み、終わり x_ini = [2; 4]; % // 初期値 xout = lsode("dotFunc",x_ini, t) clf(); % // 時間変化のプロット subplot(2,1,1) plot(t,xout(:,1),"r-") hold on; plot(t,xout(:,2),"b-") % // 軌跡のプロット subplot(2,1,2) plot(xout(:,1), xout(:,2))
微分方程式の右辺の関数をdotFuncLV.mとして
function xdot = dotFuncLV(t,x) % // Lotka-Volterra方程式 m =0.5; xdot = [x(1) - x(1)*x(2); m * (x(1)*x(2) - x(2))]; %返り値は列ベクトル endと書いておき、メインの実行ファイルを
% 時間のはじめと終わり、初期値を与えて微分方程式を計算 t0 = 0.0; t_max = 40.0; x_ini = [2; 4]; % // 初期値 [t xout] = ode23(@dotFuncLV,[t0 t_max], x_ini); % // 時間変化のプロット subplot(2,1,1) plot(t,xout(:,1),'b-',t,xout(:,2),'r-'); % // 軌跡のプロット subplot(2,1,2) plot(xout(:,1), xout(:,2))で計算できる。標準では時間刻みは自動的にセットされる。手動で与えるには、
[t xout] = ode23(@dotFuncLV,[t0: 0.01: t_max], x_ini);のように、ode23の第2引数の時刻を、t0からt_maxまでの配列として与える。
1. 行列、ベクトルの数値計算で利用したdvectorやdmatrix関数は、配列用の領域を確保し、そのポインタを返すものでした。ポインタを返すことはできますが、配列に格納された値をreturn文で返すことはできません。Cでは、呼び出す側で箱(配列)を用意し、その箱の場所(ポインタ)を関数の引数として渡し、関数内の処理で値を箱に入れるという方法を取るのが普通です。