Logistic Regression (an example)¶
これまで扱ってきたデータは、説明変数に対する目的変数の値は、平均値の周りにガウス分布すると想定してきました。しかし、目的変数に上限、下限がある場合は、平均値が上限、下限に近いときガウス分布するとは言えません。
典型例としてよく紹介されるのは、学習時間を説明変数、試験の合否を目的変数にとるような場合です。この場合、目的変数は2値ですが、同じ時間勉強しても合格者も不合格者も一定割合ででるでしょう。その確率分布はどのようになるか、また合格可能性を勉強時間の関数とした数値で表すにはどうしたらよいでしょう。
WikipediaのLogistic Regressionでは、その例が載っています。

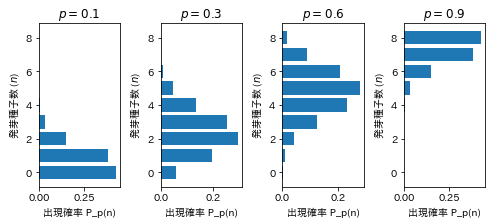
合格可能性を$p$とすると合格者数の分布は次のような二項分布になると想定されます。このような場合は、サンプル集団の合格者数分布は合格可能性曲線の上下でガウス分布のような対称な形とはなりません。その意味では「平均」としての合格可能性の意味には慎重な解釈が必要になります。 (この図(ヒストグラム)を作成するプログラムは、下の「参考」に掲載。)
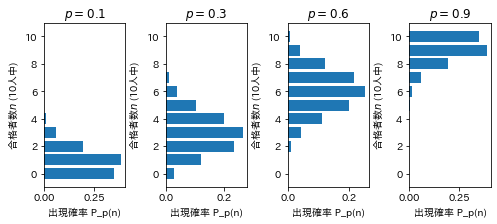
同じような問題ですが、
この授業では、生態学でのサンプルデータを扱ってみます。
「データ解析のための統計モデリング入門」(久保拓弥、岩波)の著者ページにリンクがある、著者の講義ノート https://kuboweb.github.io/-kubo/ce/EesLecture2008.html#toc5 からの引用です。
上記ページでは統計処理言語Rのプログラム例が載っていますが、ここではpythonで分析を試みます。