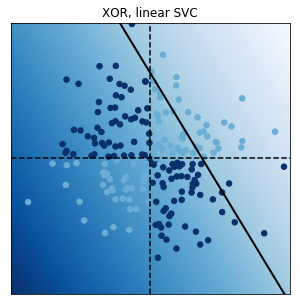
# We generate a grid in the square [-3,3 ]^2.
xx, yy = np.meshgrid(np.linspace(-3, 3, 500),
np.linspace(-3, 3, 500))
# This function takes a SVM estimator as input.
def plot_decision_function(est, title):
# evaluate the decision function on the grid.
Z = est.decision_function(np.c_[xx.ravel(),
yy.ravel()])
Z = Z.reshape(xx.shape)
cmap = plt.cm.PiYG # Blues
# We display the decision function on the grid.
fig, ax = plt.subplots(1, 1, figsize=(8, 8))
# ax.imshow(Z,
# extent=(xx.min(), xx.max(),
# yy.min(), yy.max()),
# aspect='auto',
# origin='lower',
# cmap=cmap)
# We display the boundaries.
ax.contour(xx, yy, Z, levels=[0],
linewidths=2,
colors='k')
# We display the points with their true labels.
ax.scatter(X[:, 0], X[:, 1],
s=50, c=.5 + .5 * y,
edgecolors='k',
lw=1, cmap=cmap,
vmin=0, vmax=1)
ax.axhline(0, color='k', ls='--')
ax.axvline(0, color='k', ls='--')
ax.axis([-3, 3, -3, 3])
ax.set_axis_off()
ax.set_title(title)
ax.scatter(est.support_vectors_[:,0], est.support_vectors_[:,1],
facecolors='none', edgecolors='r',s=30)
# 注:"support_vectors_"にサポートベクトルに該当するデータが入っている