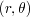 を採用する.固いかたまりなので,回転にあたって
を採用する.固いかたまりなので,回転にあたって
 は変化しない定数であり,
は変化しない定数であり,
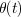 は時間の関数である.
は時間の関数である.これまでの章では,物体は「点」として扱ってきたが,この章以降は,形のある物体の運動について考える.その意味で,急に難しくなる.
- まず,最初に形がかわらない「固い」物体を考える.これを剛体と呼ぶ.
- 飛んでいる剛体の運動は,重心の運動と重心回りの回転運動に分けられる.もし回転がなければ,点の運動と同じに扱える.この点についての詳しい説明は次の章で与えるとして,この章では,回転についてだけ扱う.
- 重心の回りの回転にこだわらず,ある点を中心とした回転を考える.回転の中心は固定し,回転軸も固定されている場合のみを扱ってみよう.
- 中心や軸が変らず,形も変らないのであるから,回転は,どれだけの速さで回転しているかだけが問題となる.
ある点の位置を表すために,極座標
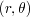 を採用する.固いかたまりなので,回転にあたって
を採用する.固いかたまりなので,回転にあたって
 は変化しない定数であり,
は変化しない定数であり,
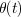 は時間の関数である.
は時間の関数である.
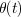 の単位時間あたりの変化量を角速度と呼ぶ.
の単位時間あたりの変化量を角速度と呼ぶ.
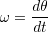
その微分を角加速度と呼ぶ.
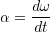
ある点の速さ v は単位時間あたりの移動距離として次のように定義できる.
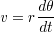
速度の向きは円の接線方向である.
加速度は,その微分で表される. r は定数であるから
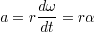
である.
角速度が一定(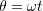 ,ωは一定)の場合,加速度は動径方向を向いている.このことを,点Pの位置を直交座標で表し、その微分により速度,加速度を表すことをつうじて理解しよう.
,ωは一定)の場合,加速度は動径方向を向いている.このことを,点Pの位置を直交座標で表し、その微分により速度,加速度を表すことをつうじて理解しよう.
位置の直交座標は,rと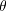 を用いて
を用いて
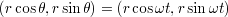
と表される.直交座標での速度は,それぞれの成分ごとに微分すれば良いから
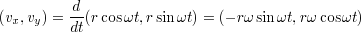
と書ける.同様に加速度は
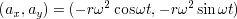
位置と加速度を見比べると
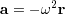
の関係があることがわかる.つまり, a と r は平行であり中心方向を向いている.ここで導いたことは,角速度が一定である場合についてであることに注意しよう.角速度を増加/減少させるには,円周方向の力が必要である. 授業ではそのような場合についても扱ってみる.
剛体が回転運動をしているとき,剛体全体の運動エネルギーを考えてみよう.大事な点は,すべての部分が同じ角速度を持っているということである.
剛体を細かく分け,それらにラベル i をつけることにすると,剛体全体の運動エネルギーは
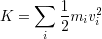
と書ける.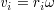 を代入すると,
を代入すると, は和の外に出せて
は和の外に出せて
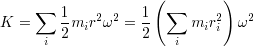
となる.
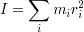
と書けば,
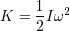
と表される. I を 慣性モーメント と呼ぶ.
I は回転運動における質量のようなイメージでとらえてもよい.手動で物体を同じ回転角速度にする場合の「おもさ」のような感覚である.同じ質量でも回転半径が大きい場合は回転させる場合,重いと感ずるであろう.そのイメージである.
同じ質量の物体でも中空で円環上に質量が分布している場合と,中身がつまった円筒や球の場合とでは,慣性モーメントが異なる.典型的な例についてそれを計算してみる.
慣性モーメントの計算は,剛体の各部分の質量と「半径」の2乗の「和」をとることである.
結果は図10.2にまとめられている.
図10.15のように,半径 r の質量のゼロの腕につながれた質量 m の物体の回転運動を考えよう.腕の長さが変化しない(もっとも簡単な剛体)のであらるから,運動の変化に影響する力は円周の接線方向の力だけである.この力の大きさを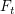 と書く.これと円周方向の加速度
と書く.これと円周方向の加速度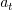 の間には
の間には
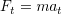
の関係がある.式を慣性モーメント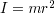 と角加速度
と角加速度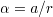 を用いて書き換えると
を用いて書き換えると
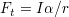
r を両辺にかけると

という関係が得られる.τをトルク(回転力)と呼ぶ.
一般に中身がつまった剛体においても同じ関係が成り立つ(10.20式).
言葉で書けば
(慣性モーメント)×(角加速度) = (トルク)
となり,これらを用いると,形式的にニュートンの運動方程式ときれいに対比できる関係式が得られる(表10.3).
前節と同様,回転中心から半径rにある部分に力 F がはたらき,回転運動(半径方向には動かない)をするとすると,その部分になされる仕事は
と表される.2つめの等号は,動いた距離と動いた方向の力の積として前節で用いた 円周方向の力と微小回転角を用いた書き換えである.
仕事の結果は回転の運動エネルギー変化である.
回転加速度を
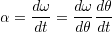
トルクと角加速度の関係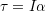 用いると
用いると
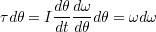
を書ける.つまり
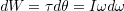
である.これを積分すると,回転エネルギーの変化高になる.回転角速度ゼロを基準にすると,回転の運動エネルギーは
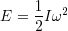
と表される.
前の節において,速度を角速度を用いて表して,運動エネルギーの表式を書き換えた結果と同じである.