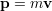
運動量を
と定義するとニュートンの運動方程式は
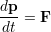
と書ける．これを時刻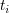
から
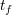まで積分すると形式的に
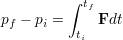
と書ける．運動量の変化は，この時間範囲について力を積分した量に等しいことがわかる．右辺を力積(impulse)という．
これはどのような力であっても成り立ち，ある時間区間の初めと終わりの運動量がわかれば，トータルとしてどれだけの力が働いたかがわかる．逆に言えば，力の働き方の詳細によらない法則性を見いだすことができる．それが次の節の「運動量保存則」である．
その前に，直接には測れない力の大きさを見積もる問題（例題９．１と練習１）をやってみよう．9.1の(b)は答を読んでしまうそれほど難しく感じないかもしれないが，ヒントがなしで解くのにはセンスが必要な問題である．（「接触したまま運動する距離はボールの半径程度」と見積もるのにはセンスがいる．）
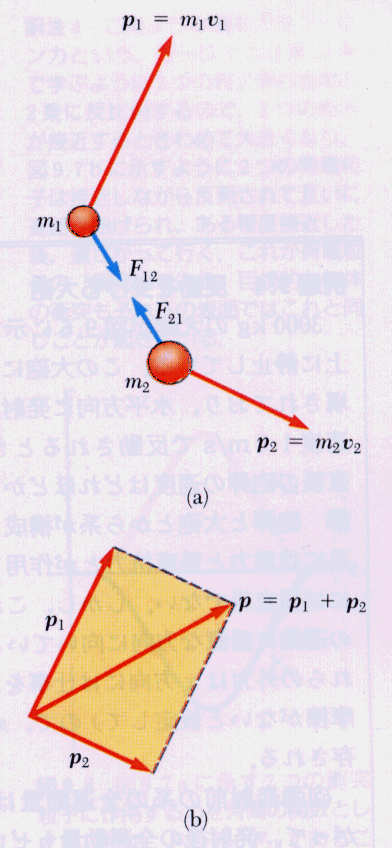
図のような２つの質点間に力が働いている場合を考えよう．相互作用力には作用・反作用の法則が成り立つことがポイントである．
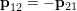
それぞれの点に外部から働く力（外力external force)と呼ぶ）を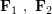
とすると，運動方程式は
両式を足し，作用・反作用の法則を適用すると
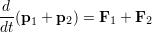
となる．外力が働かない（右辺の力がゼロ）ときには
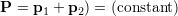
が得られる．つまり
系の外から力が働かないとき，全体の運動量は一定に保たれる
のである．これを運動量保存則という．
[参考] JAXA 若田光一宇宙飛行士の宇宙実験 http://iss.jaxa.jp/iss/jaxa_exp/wakata/omoshiro/
この節では，力が働いている短い時間のできごとの詳細にはかかわらないで，その前後の運動量の関係を定式化する．
そとから力が働いていなければ，運動量は保存するが，エネルギーは保存される場合もあるし，されない場合もある．
衝突後，衝突した物体が合体して運動する場合を，完全非弾性衝突という．
衝突後の速度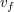
を衝突前のそれぞれの速度と質量を用いて表してみよう．（各自）
未知数が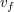だけなので，運動量保存則を用いて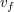を求めることができる．
エネルギー保存則がなりたつ場合を弾性衝突と呼ぶ．衝突前の質量と速度が与えられていれば，運動量保存則，エネルギー保存則という２つの式より，未知数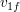
と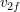
を決定することができる．
一般の非弾性衝突の場合は，衝突によってどの割合のエネルギーが失われるかを与えることにより，衝突後の速度を決められる．
授業では定性的にだけ触れることにする．
何次元であっても運動量保存則はなりたつ．前に触れたように，ベクトルの各成分ごとに運動量保存則の関係式を書くことができる．
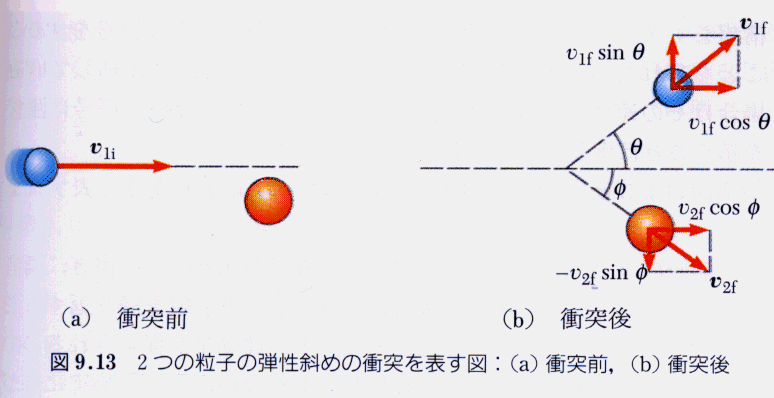
General Physics Java Applets中のCollisionシミュレーションで衝突の様子を確かめてみよう．
２つの質点について，２つの質点の位置を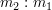
に内分する点を質量中心(重心)と呼ぶ．位置をベクトルで表せば，
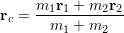と書ける．
のように運動方程式が書かれるとき，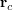
の時間変化を調べてみよう．
結果として，
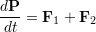
となる．ただし，
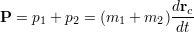
は，系の全運動量を表す．
系全体としては，質量中心に全部の質量が集まっており，そこに全外力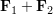
が働いてるのと同じ方程式である．
多質点系についても同様な式を書くことができる．
系の外から力が働かないときは，質量中心は等速直線運動をする． その例重心の運動が9.23図にある．
General Physics Java Applets中の"Ceter of Mass"のシミュレーションで重心の運動の様子を確かめてみよう．
章末問題 2,3,4, 13,18,19,27,58